贪心算法----区间选点问题(POJ1201)

题目：

　　

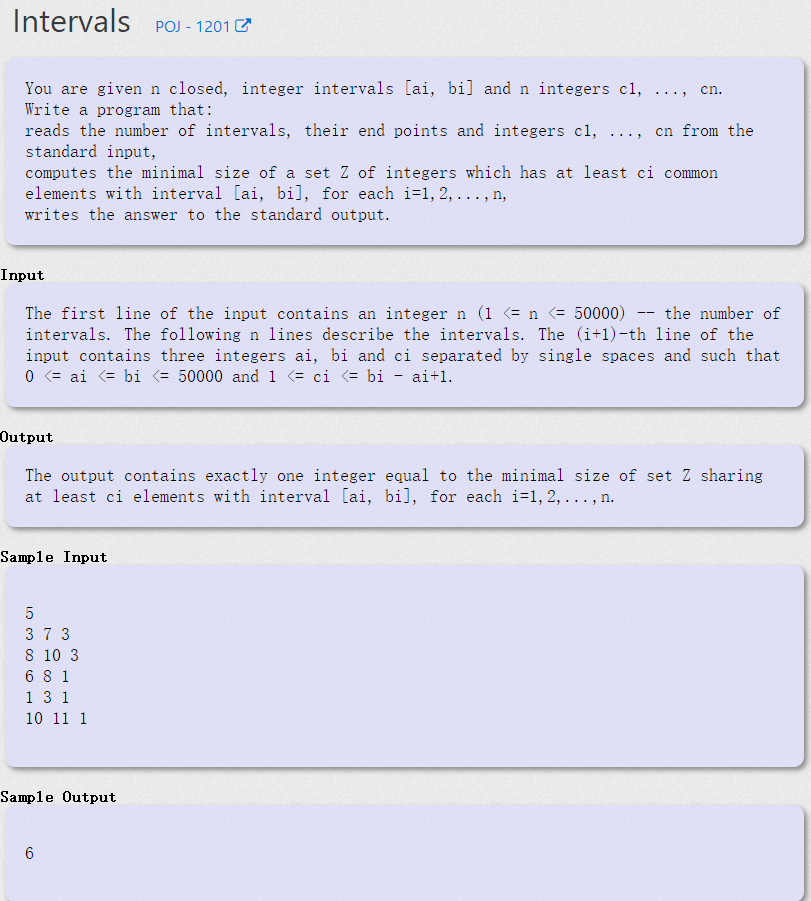
　　题目的大致意思是，给定n个闭区间，并且这个闭区间上的点都是整数，现在要求你使用最少的点来覆盖这些区间并且每个区间的覆盖的点的数量满足输入的要求点覆盖区间的数量。

　　输入：

　　　　第一行输入n，代表n个区间。

　　　　接下来的n行每行的第一个数代表区间起点，第二个数代表区间终点，第三个数代表这个区间必须要选取的点的数量。

　　输出：

　　　　输出最少的点的数量，这些最少的点要覆盖全部区间。

　　这个题是区间选点问题的一种变体，但是我们对于区间选点问题清楚之后那么这种题目也是一样解决的，只不过需要在某些地方特别处理一下。这道题目跟区间调度的问题非常类似，我们也可以采用区间调度问题的策略运用到这道题目上面，尽量往结束时间的端点来选点因为这样做我们可以使尽量少的点覆盖更多的区间，之后就是选点的问题了，当我们选择了这个点之后需要标记一下，定义一个数轴来记录其中标记过的点，以防下一次在选点的时候重复选择。而且在for循环中依次扫描这些给定的区间，看这个区间需要覆盖的点的数量是多少（有可能这个区间的标记的点出现在另外的区间上那么这个时候我们就选择跳过这个点）

　　代码：

 import java.util.Arrays;
 import java.util.Scanner;

 public class 区间选点问题1 {
     public static void main(String[] args) {
         Scanner sc = new Scanner(System.in);
         int n = sc.nextInt();
         Interval[] intervals = new Interval[n];
         for (int i = 0; i < n; i++) {
             intervals[i] = new Interval(sc.nextInt(), sc.nextInt(), sc.nextInt());
         }
         Arrays.sort(intervals);// 按区间右端点排序

         int max = intervals[n - 1].t;// 右端最大值
         int[] axis = new int[max + 1];// 标记数轴上的点是否已经被选中
         // int[] sums = new int[max + 1];
         for (int i = 0; i < n; i++) {
             // 1.查阅区间中有多少个点
             int s = intervals[i].s;// 起点
             int t = intervals[i].t;// 终点
             int cnt = sum(axis, s, t);// 找到这个区间已经选点的数量，
                                         //sums[t] - sums[s - 1]; 效率低
             // 2.如果不够，从区间右端开始标记，遇标记过的就跳过
             intervals[i].c -= cnt;// 需要新增的点的数量
             while (intervals[i].c > 0) {
                 if (axis[t] == 0) {// 从区间终点开始选点
                     axis[t] = 1;
                     // updateSums(t,sums);//更新前缀和
                     intervals[i].c--;// 进一步减少需要新增的点的数量
                     t--;
                 } else {// 这个点已经被选过了
                     t--;
                 }
             }

         }
         System.out.println(sum(axis, 0, max));
     }

     /**
      * 统计数轴axis上s-t区间已经有多少个点被选中
      *
      * @param axis
      * @param s
      * @param t
      * @return
      */
     private static int sum(int[] axis, int s, int t) {
         int sum = 0;
         for (int i = s; i <= t; i++) {
             sum += axis[i];
         }
         return sum;
     }

     private static void updateSums(int t, int[] sums) {
         for (int i = t; i < sums.length; i++) {
             sums[i]++;
         }
     }

     private static class Interval implements Comparable<Interval> {
         int s;
         int t;
         int c;

         public Interval(int s, int t, int c) {
             this.s = s;
             this.t = t;
             this.c = c;
         }

         @Override
         public int compareTo(Interval other) {
             int x = this.t - other.t;
             if (x == 0)
                 return this.s - other.s;
             else
                 return x;
         }
     }
 }

　　结果：

　　　　

　　但是上面这个代码提交到OJ上面会发生超时，代码逻辑本身没有什么问题，关键是在扫描每个区间的时候消耗的时间比较多导致了超时，但是我们可以使用另外的一种数据结构来解决，那就是树状数组，降低扫描区间的时间复杂度。关于树状数组现在不太懂，而且也脱离了贪心算法的范畴，现在把代码记录下来，留作以后再看。

　　代码：

 import java.util.Arrays;
 import java.util.Scanner;

 public class 区间选点问题2 {
     public static void main(String[] args) {
         Scanner sc = new Scanner(System.in);
         int n = sc.nextInt();
         Interval[] intervals = new Interval[n];
         for (int i = 0; i < n; i++) {
             intervals[i] = new Interval(sc.nextInt(), sc.nextInt(), sc.nextInt());
         }
         Arrays.sort(intervals);// 按区间右端点排序

         int max = intervals[n - 1].t;// 右端最大值
         int[] axis = new int[max + 1];
         int[] c = new int[max + 2];
         // int[] sums = new int[max + 1];
         for (int i = 0; i < n; i++) {
             // 1.查阅区间中有多少个点
             int s = intervals[i].s;// 起点
             int t = intervals[i].t;// 终点
             int cnt = sum(t + 1, c, max + 1) - sum(s, c, max + 1);// sum(axis,s,t);//sums[t]
                                                                     // - sums[s
                                                                     // -
                                                                     // 1];//效率低
             // 2.如果不够，从区间右端开始标记，遇标记过的就跳过
             intervals[i].c -= cnt;
             while (intervals[i].c > 0) {
                 if (axis[t] == 0) {
                     axis[t] = 1;
                     update(t + 1, 1, c, max + 1);
                     intervals[i].c--;
                     t--;
                 } else {
                     t--;
                 }
             }

         }
         System.out.println(sum(max + 2, c, max + 1));
     }

     /**
      * 更新树状数组c，注意i是项数，不是下标，而是下标+1
      */
     private static void update(int i, int delta, int[] c, int n) {
         for (; i <= n; i += lowbit(i)) {
             c[i] += delta;
         }
     }

     /**
      * 前i项和，注意：i不是下标
      *
      * @param i
      * @return
      */
     private static int sum(int i, int[] c, int n) {
         int sum = 0;
         if (i > n)
             i = n;
         for (; i > 0; i -= lowbit(i)) {
             sum += c[i];
         }
         return sum;
     }

     /**
      * 它通过公式来得出k，其中k就是该值从末尾开始1的位置。 然后将其得出的结果加上x自身就可以得出当前节点的父亲节点的位置
      * 或者是x减去其结果就可以得出上一个父亲节点的位置。
      * 比如当前是6，二进制就是0110，k为2，那么6+2=8，C(8)则是C(6)的父亲节点的位置；
      * 相反，6-2=4，则是C(6)的上一个父亲节点的位置。
      */
     static int lowbit(int x) {
         return x - (x & (x - 1));
     }

     private static class Interval implements Comparable<Interval> {
         int s;
         int t;
         int c;

         public Interval(int s, int t, int c) {
             this.s = s;
             this.t = t;
             this.c = c;
         }

         @Override
         public int compareTo(Interval other) {
             int x = this.t - other.t;
             if (x == 0)
                 return this.s - other.s;
             else
                 return x;
         }
     }
 }