UOJ#201. 【CTSC2016】单调上升路径 构造

原文链接https://www.cnblogs.com/zhouzhendong/p/UOJ201.html

题解

首先把题目里面的提示抄过来：

结论：假设带权无向图 G 有 100 个节点 1000 条边，且所有权值各不相同。那么，G 中一定存在一个单调上升路径，它的长度大于等于 20。

证明：假设每个节点上有一个探险家。我们按权值从小到大枚举所有的边，每次将该边连接的节点中的探险家的位置进行对调。可以知道，每个探险家都走的是一条单调上升路径。另外，由于共有 100 个探险家，而探险家一共走了 2000 步，所以有人走了 20 步。证毕。

于是容易得知点数为 n 的完全图至少要走 n-1 步。

注意到 n 为偶数，那么我们来构造一下走n-1步的图。

我们考虑把所有的边分成 (n-1) 个大小为 n/2 的集合且同组的边没有端点重合。

于是我们只要把第一组标 1..n/2 ，第二组标 n/2+1...n， .... 即可。

关键是怎么构造。

看图：

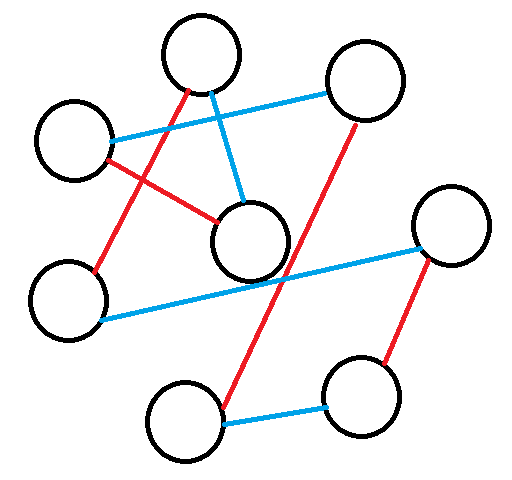
这里红的一组，蓝的一组，总共就类似这样的转 n-1 次就好了。

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
LL read(){
	LL x=0;
	char ch=getchar();
	while (!isdigit(ch))
		ch=getchar();
	while (isdigit(ch))
		x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
	return x;
}
const int N=505;
int n,k;
int cnt=0;
int g[N][N];
int nxt(int x){
	return x==k?1:x+1;
}
int pre(int x){
	return x==1?k:x-1;
}
int main(){
	n=read();
	k=n-((n&1)^1);
	for (int i=1;i<=k;i++){
		if (~n&1)
			g[n][i]=g[i][n]=++cnt;
		int x=i,y=i;
		for (int j=1;j<=(n-1)/2;j++){
			x=pre(x),y=nxt(y);
			g[x][y]=g[y][x]=++cnt;
		}
	}
	for (int i=1;i<=n;i++)
		for (int j=i+1;j<=n;j++)
			printf("%d ",g[i][j]);
	return 0;
}