304. Range Sum Query 2D - Immutable(动态规划)

Given a 2D matrix matrix, find the sum of the elements inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).

The above rectangle (with the red border) is defined by (row1, col1) = (2, 1) and (row2, col2) = (4, 3), which contains sum = 8.

Example:

Given matrix = [
  [3, 0, 1, 4, 2],
  [5, 6, 3, 2, 1],
  [1, 2, 0, 1, 5],
  [4, 1, 0, 1, 7],
  [1, 0, 3, 0, 5]
]

sumRegion(2, 1, 4, 3) -> 8
sumRegion(1, 1, 2, 2) -> 11
sumRegion(1, 2, 2, 4) -> 12

Note:

1. You may assume that the matrix does not change.
2. There are many calls to sumRegion function.
3. You may assume that row1 ≤ row2 and col1 ≤ col2.

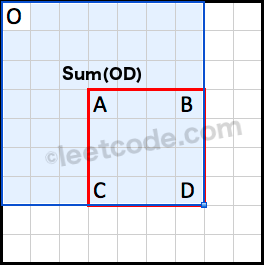
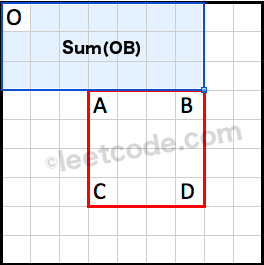
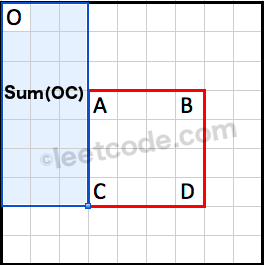
Sum(ABCD)=Sum(OD)−Sum(OB)−Sum(OC)+Sum(OA)

ps: 注意dp的递推公式

 class NumMatrix {
 public:
     vector<vector<int>> dp;

     NumMatrix(vector<vector<int>> matrix) {
         int n =matrix.size();
         int m = n==?:matrix[].size();

         dp = vector<vector<int>>(n+,vector<int>(m+,));
         for(int i =  ;i<n;i++)
             for(int j = ;j<m;j++){
                 dp[i+][j+] = dp[i][j+]+dp[i+][j]-dp[i][j]+matrix[i][j];
             }
     }

     int sumRegion(int rows1, int cols1, int rows2, int cols2) {
         return dp[rows2+][cols2+] - dp[rows1][cols2+] - dp[rows2+][cols1] +dp[rows1][cols1];
     }
 };

 /**
  * Your NumMatrix object will be instantiated and called as such:
  * NumMatrix obj = new NumMatrix(matrix);
  * int param_1 = obj.sumRegion(row1,col1,row2,col2);
  */