spring的配置与使用

一、Spring介绍

1. 什么是Spring

Spring是一个开源框架,Spring是于2003 年兴起的一个轻量级的Java 开发框架，由 RodJohnson 在其著作 Expert One-On-One J2EE Development and Design 中阐述的部分理念和原型衍生而来。它是为了解决企业应用开发的复杂性而创建的。框架的主要优势之一就是其分层架构，分层架构允许使用者选择使用哪一个组件，同时为 J2EE 应用程序开发提供集成的框架。Spring 使用基本的 JavaBean 来完成以前只可能由 EJB 完成的事情。然而，Spring 的用途不仅限于服务器端的开发，去开发android也可以。从简单性、可测试性和松耦合的角度而言，任何 Java 应用都可以从 Spring 中受益。Spring 的核心是控制反转 (IoC)和面向切面(AOP)。简单来说，Spring 是一个分层的 JavaSE/EEfull-stack(一站式) 轻量级开源框架。

2. 为什么要学习Spring

方便解耦，简化开发
- Spring 就是一个大工厂，可以将所有对象创建和依赖关系维护，交给 Spring 管理
AOP 编程的支持
- Spring 提供面向切面编程，可以方便的实现对程序进行权限拦截、运行监控等功能
声明式事务的支持
- 只需要通过配置就可以完成对事务的管理,而无需手动编程
方便程序的测试
- Spring 对 Junit4 支持,可以通过注解方便的测试 Spring 程序
方便集成各种优秀框架
- Spring 不排斥各种优秀的开源框架,其内部提供了对各种优秀框架(如:Struts、Hibernate、MyBatis、Quartz 等)的直接支持降低 JavaEE API 的使用难度
Spring 对 JavaEE 开发中非常难用的一些 API(JDBC、JavaMail、远程调用等)，都提供了封装，使这些 API 应用难度大大降低。

3. Spring 的版本

Spring 3.X 和 Spring4.X

Spring 3.0.2版本：将市面上常见的、支持整合进来的工具类全部进行了收录，这个包里面有很多很多jar包。但是这是Spring坚持“做好事”的最后一个版本，没有任何回报。

1. IOC思想和DI技术

（1）IOC (Inverse Of Control)：控制反转，将我们创建对象的方式反转了。

以前对象的创建是由开发人员自己维护，包括依赖关系也是自己注入。使用了Spring之后，对象的创建以及依赖关系可以由Spring完成创建以及注入。

（2）DI(Dependency Injection)：依赖注入。将必须的属性注入到对象当中，是实现IOC思想的必要条件。

需要有 IOC 的环境，Spring 创建这个类的过程中，Spring 将类的依赖的属性设置进去。

2. Spring中的工厂(容器)

（1）ApplicationContext

ApplicationContext接口有两个实现类：

ClassPathXmlApplicationContext :加载类路径下 Spring 的配置文件
FileSystemXmlApplicationContext :从绝对路径上加载本地磁盘下 Spring 的配置文件，基本用不着。

3. Spring生成Bean的三种方式（三种对象创建方式）

对象的创建必须经过类的构造函数。

（1）空参构造创建 --最重要

在上面示例中的User对象中加一个无参构造函数

重新创建一个包，把applicationContext.xml复制进该包中，把测试类testSpringDemo.java复制进该包中，并修改该文件中applicationContext.xml的位置。

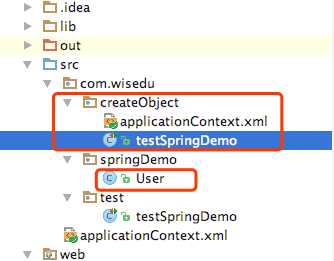
具体代码如下：

User.java

applicationContext.xml

testSpringDemo.java