lillietest 正态分布的拟合优度测试

函数 lillietest
格式 H = lillietest(X) %对输入向量X进行Lilliefors测试,显著性水平为0.05.
H = lillietest(X,alpha) %在水平alpha而非5%下施行Lilliefors测试,alpha在0.01和0.2之间.
[H,P,LSTAT,CV] = lillietest(X,alpha) %P为接受假设的概率值,P越接近于0,则可以拒绝是正态分布的原假设;LSTAT为测试统计量的值,CV为是否拒绝原假设的临界值.
说明 H为测试结果,若H=0,则可以认为X是服从正态分布的;若X=1,则可以否定X服从正态分布.

Y=chi2rnd(10,100,1);
[h,p,l,cv]=lillietest(Y)

h =

     1

p =

   1.0000e-03

l =

    0.1255

cv =

    0.0890

说明 h=1表示拒绝正态分布的假设;p = 0.0175表示服从正态分布的概率很小;统计量的值l = 0.1062大于接受假设的临界值cv =0.0886,因而拒绝假设(测试水平为5%).

figure(1);
hist(Y);   %作频数直方图
figure(2);
normplot(Y);  %分布的正态性检验

　　

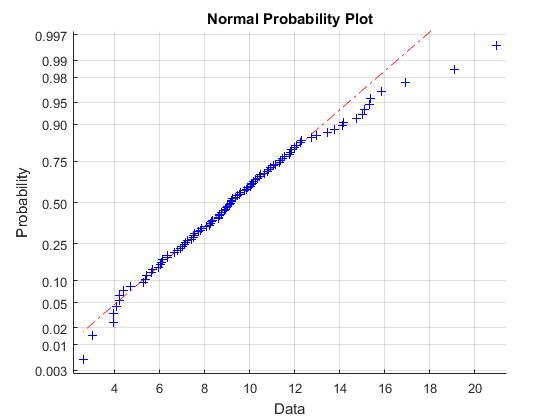
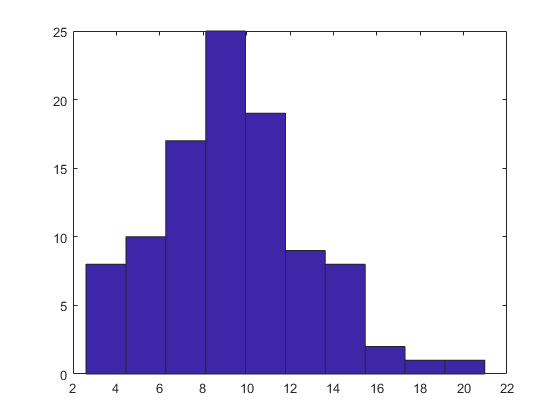
从图中看出,数据Y不服从正态分布.