OO第一单元总结与心得体会

一、结构度量

1. UML类图

第一次作业

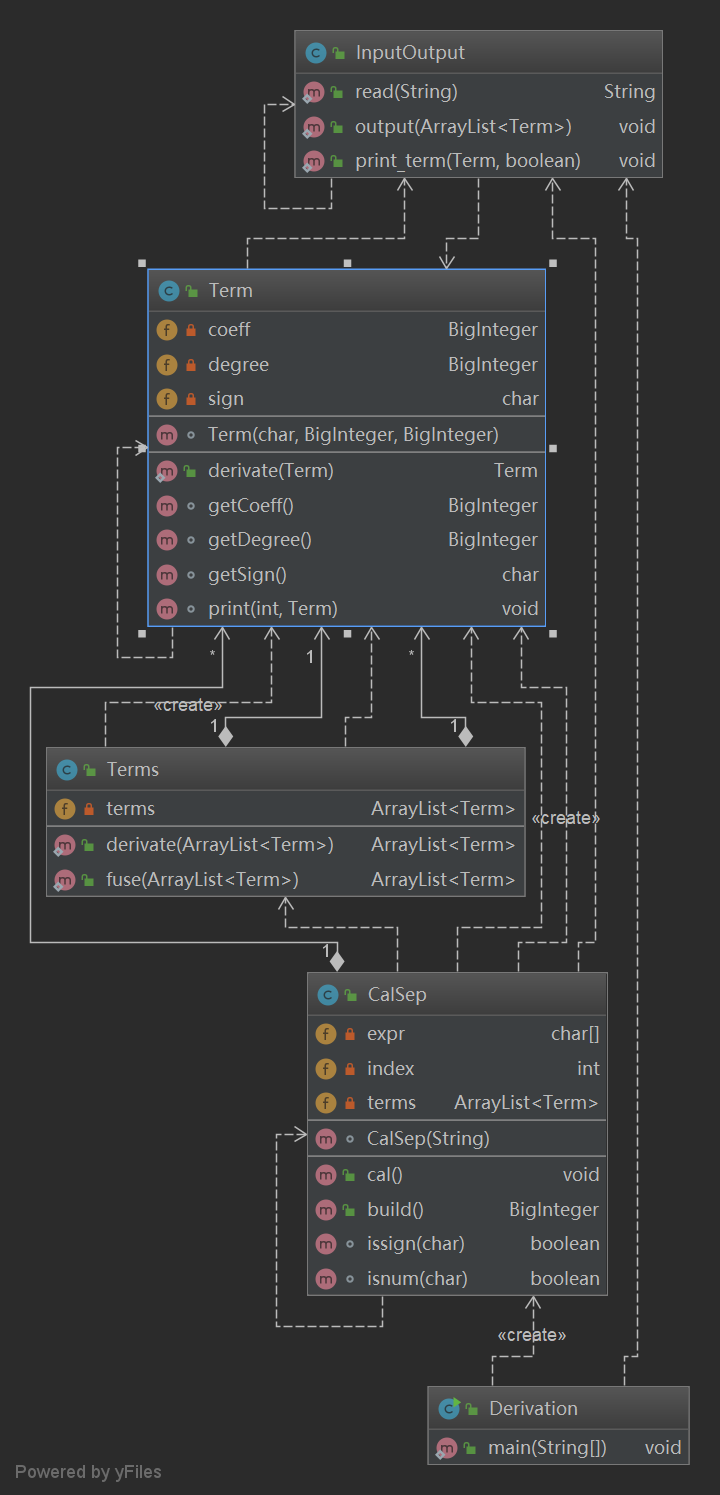
第二次作业

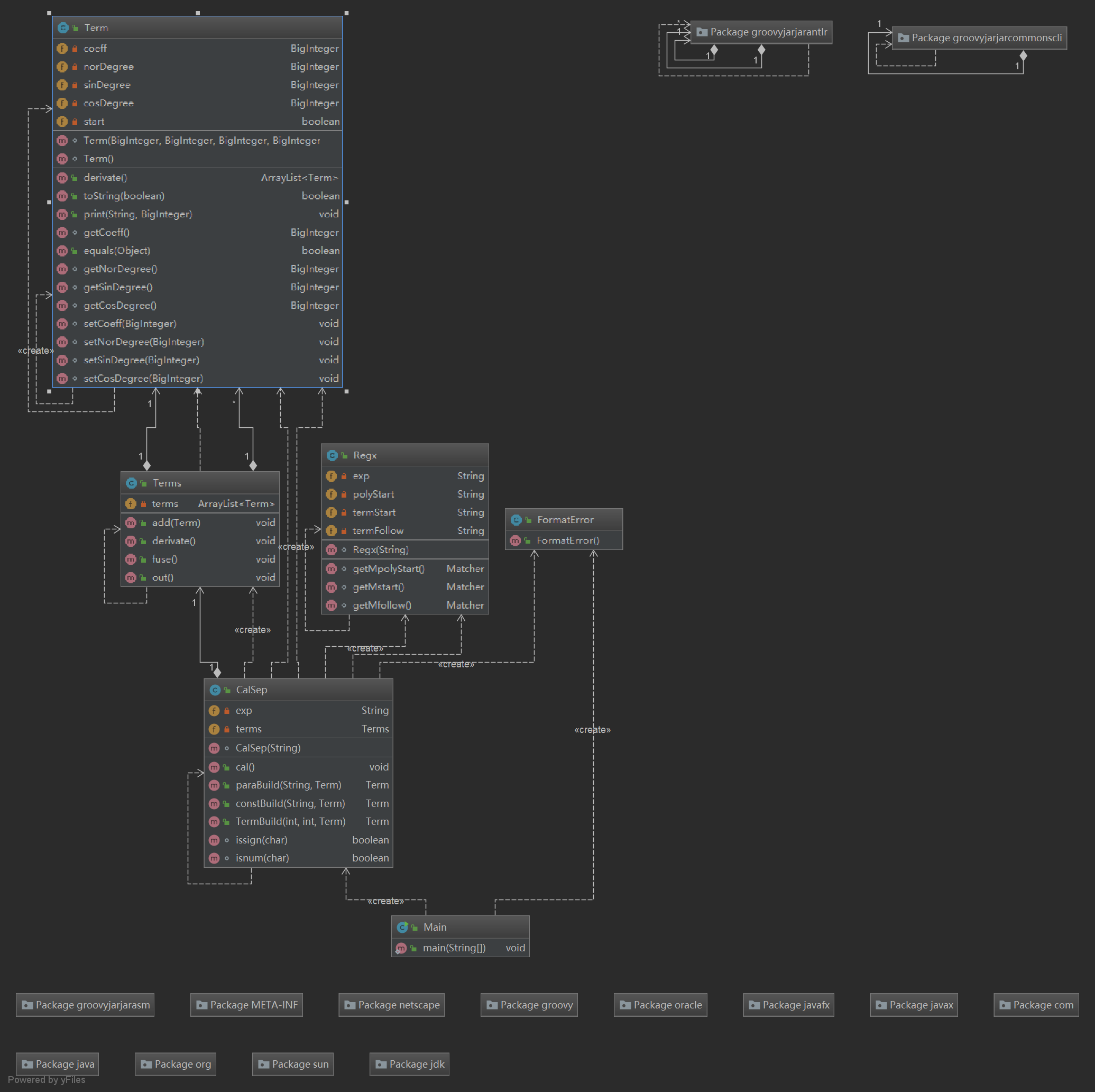
第三次作业

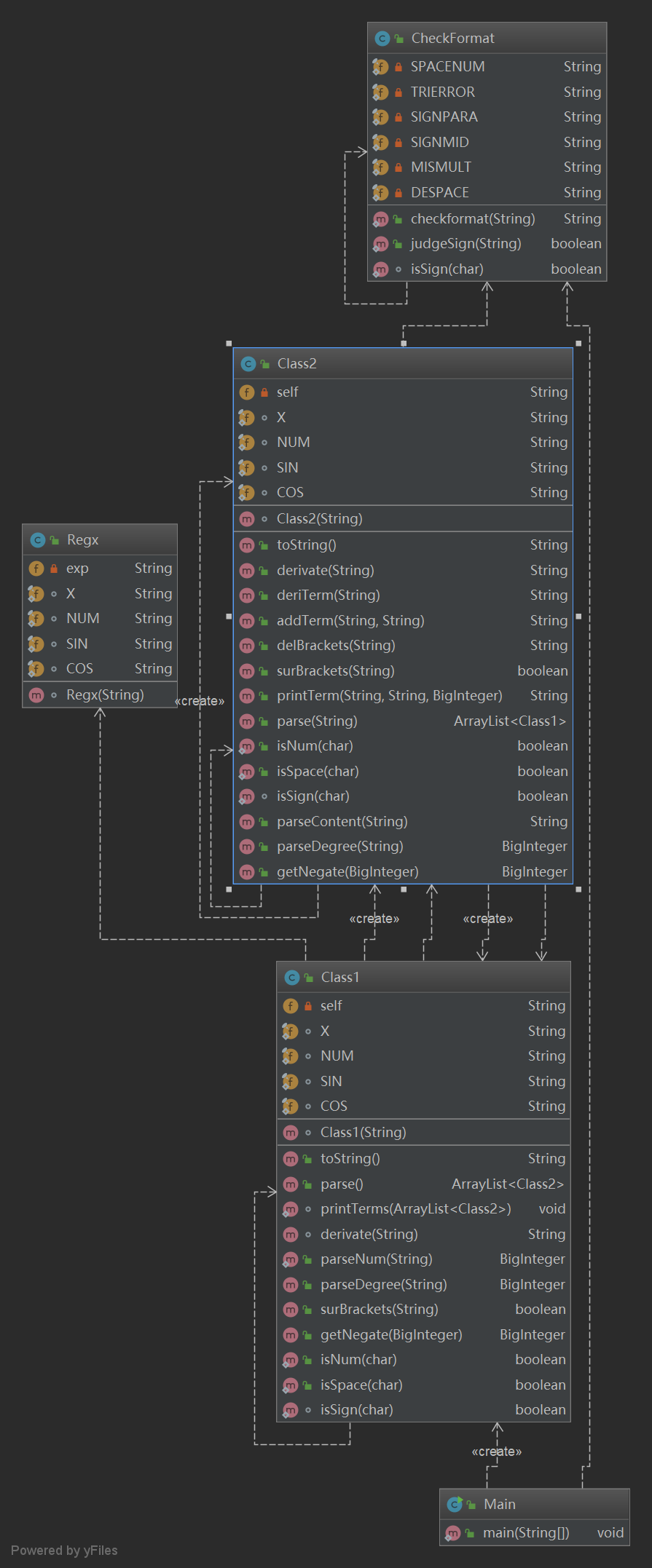
2. 复杂度分析

（1）方法复杂度

ev, iv, v这几栏，分别代指基本复杂度（Essential Complexity (ev(G))、模块设计复杂度（Module Design Complexity (iv(G))）、Cyclomatic Complexity (v(G))圈复杂度。

ev(G)基本复杂度是用来衡量程序非结构化程度的，非结构成分降低了程序的质量，增加了代码的维护难度，使程序难于理解。因此，基本复杂度高意味着非结构化程度高，难以模块化和维护。实际上，消除了一个错误有时会引起其他的错误。

Iv(G)模块设计复杂度是用来衡量模块判定结构，即模块和其他模块的调用关系。软件模块设计复杂度高意味模块耦合度高，这将导致模块难于隔离、维护和复用。模块设计复杂度是从模块流程图中移去那些不包含调用子模块的判定和循环结构后得出的圈复杂度，因此模块设计复杂度不能大于圈复杂度，通常是远小于圈复杂度。

v(G)是用来衡量一个模块判定结构的复杂程度，数量上表现为独立路径的条数，即合理的预防错误所需测试的最少路径条数，圈复杂度大说明程序代码可能质量低且难于测试和维护，经验表明，程序的可能错误和高的圈复杂度有着很大关系。

第一次作业
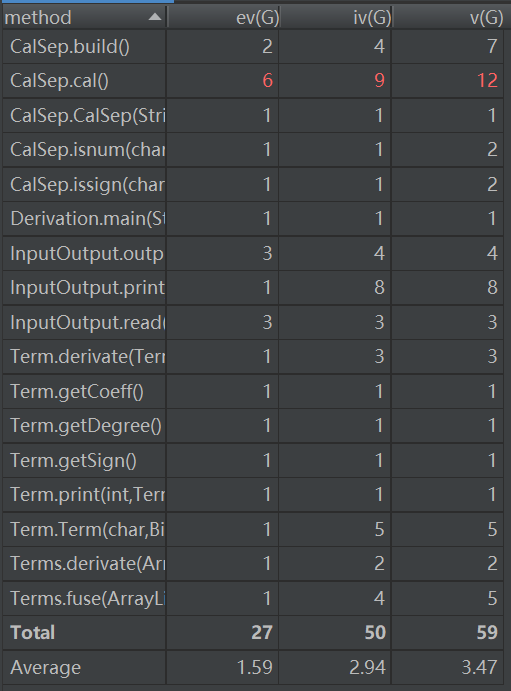
第二次作业

Method	ev(G)	iv(G)	v(G)
CalSep.CalSep(String)	1	1	1
CalSep.TermBuild(int,int,Term)	1	2	2
CalSep.cal()	10	4	10
CalSep.constBuild(String,Term)	1	6	6
CalSep.isnum(char)	1	1	2
CalSep.issign(char)	1	1	2
CalSep.paraBuild(String,Term)	1	12	12
FormatError.FormatError()	1	1	1
Main.main(String[])	1	1	2
Regx.Regx(String)	1	1	1
Regx.getMfollow()	1	1	1
Regx.getMpolyStart()	1	1	1
Regx.getMstart()	1	1	1
Term.Term()	1	1	1
Term.Term(BigInteger,BigInteger,BigInteger,BigInteger)	1	1	1
Term.derivate()	1	1	1
Term.equals(Object)	1	3	3
Term.getCoeff()	1	1	1
Term.getCosDegree()	1	1	1
Term.getNorDegree()	1	1	1
Term.getSinDegree()	1	1	1
Term.print(String,BigInteger)	2	6	7
Term.setCoeff(BigInteger)	1	1	1
Term.setCosDegree(BigInteger)	1	1	1
Term.setNorDegree(BigInteger)	1	1	1
Term.setSinDegree(BigInteger)	1	1	1
Term.toString(boolean)	2	6	7
Terms.add(Term)	1	1	1
Terms.derivate()	1	3	3
Terms.fuse()	1	4	5
Terms.out()	1	3	4

第三次作业

Method	ev(G)	iv(G)	v(G)
CheckFormat.checkformat(String)	4	7	10
CheckFormat.isSign(char)	1	1	2
CheckFormat.judgeSign(String)	3	4	5
Class1.Class1(String)	1	1	1
Class1.derivate(String)	1	2	3
Class1.getNegate(BigInteger)	1	1	1
Class1.isNum(char)	1	1	2
Class1.isSign(char)	1	1	2
Class1.isSpace(char)	1	1	2
Class1.parse()	2	10	11
Class1.parseDegree(String)	3	2	3
Class1.parseNum(String)	2	1	2
Class1.printTerms(ArrayList)	1	2	2
Class1.surBrackets(String)	4	4	7
Class1.toString()	1	1	1
Class2.Class2(String)	1	1	1
Class2.addTerm(String,String)	1	1	1
Class2.delBrackets(String)	1	2	2
Class2.deriTerm(String)	7	6	7
Class2.derivate(String)	2	7	7
Class2.getNegate(BigInteger)	1	1	1
Class2.isNum(char)	1	1	2
Class2.isSign(char)	1	1	2
Class2.isSpace(char)	1	1	2
Class2.parse(String)	1	10	10
Class2.parseContent(String)	5	7	12
Class2.parseDegree(String)	4	2	4
Class2.printTerm(String,String,BigInteger)	1	8	13
Class2.surBrackets(String)	4	4	7
Class2.toString()	1	1	1
Main.main(String[])	1	2	2
Regx.Regx(String)	1	1	1

（2）类复杂度

对于类，有OCavg和WMC两个项目，分别代表类的方法的平均循环复杂度和总循环复杂度。

第一次类复杂度
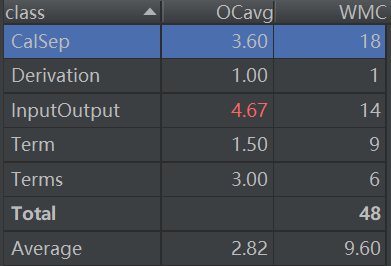
第二次类复杂度
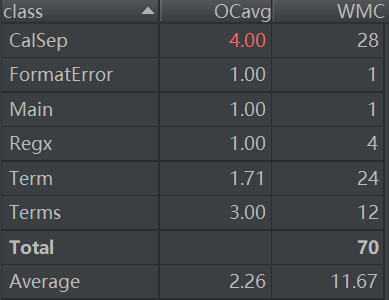
第三次类复杂度

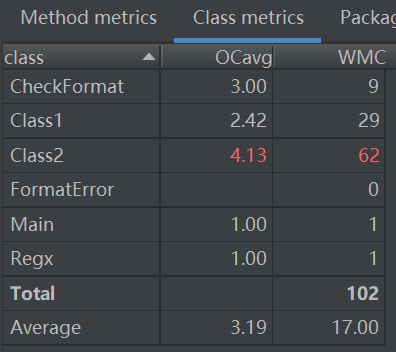
3. 依赖度分析

第一次依赖度分析

dependency
第二次依赖度分析

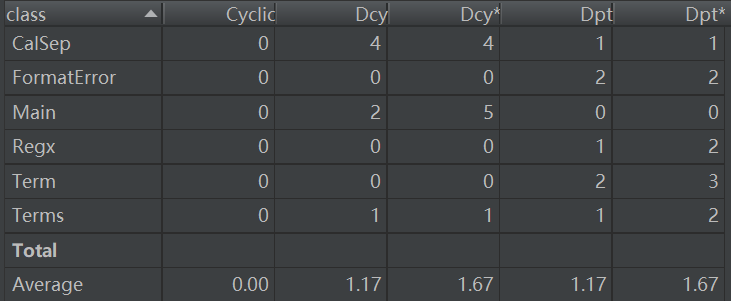dependency
第三次依赖度分析

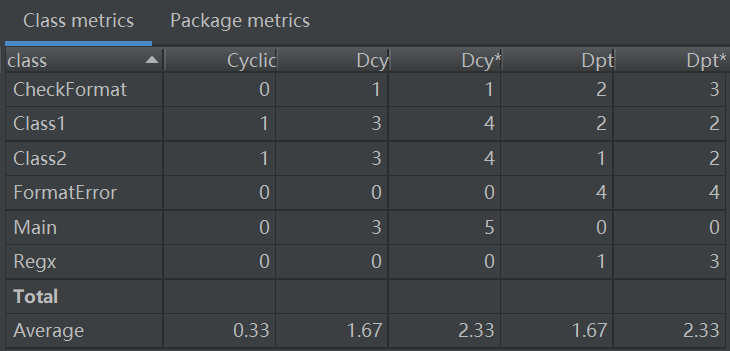dependency

（4）分析与改进

优点：类间的耦合程度较低，做到了高内聚，低耦合。
缺点：很多方法的模块化程度还不够、复杂度过高，还可以进一步细化。

参考文章：白盒测试之圈复杂度，以及可以直接降低圈复杂度的10种重构技术

首先提炼函数，将所有可被组织在一起的代码段都独立出来，并让函数名称解释该函数的用途；
合并重复的条件片段，在条件式的每个分支上的相同代码搬移到条件式之外。

修改前代码：

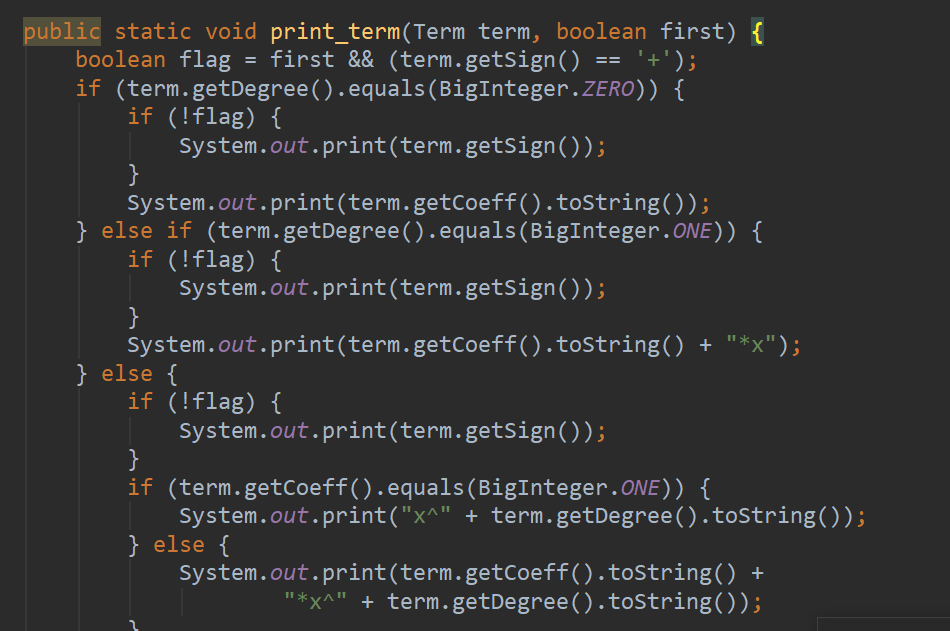
修改后代码：

修改前复杂度：

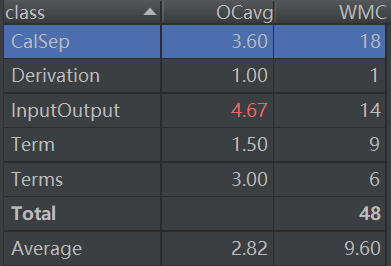
修改后复杂度：

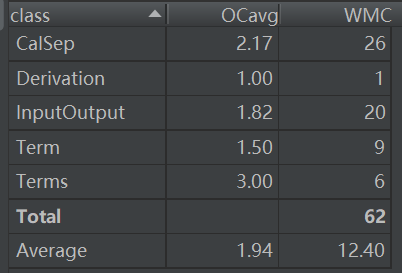
可见类复杂度明显降低。将高复杂度的代码进行适当的拆分、优化，可以大大提高代码整体的质量，减少潜在bug存在。

二、分析自己程序的bug

1. 第一次作业

第一次作业中合并同类项的算法错了，好像是下标i，j写混了.....导致合并时符号错误。

第一，这么简单的循环遍历算法都能搞错，实在是太不熟练了...第二，应用HashMap而不是数组进行储存，形成key to value的index索引思想。

2. 第二次作业

第二次没被hack到。

3. 第三次作业

0的时候不输出，出现了(())的情况，导致格式错误。
cos^n形式输出错误。因为是直接从sin那里复制过来的，所以一不注意就有各种各样的错误。还是要多注意代码的复用，不能老Ctrl-C Ctrl-V

三、分析自己发现别人程序bug所采用的策略

我发现别人程序bug主要靠构造特殊测试样例。

因为觉得完全理解别人的程序比较困难，所以没有结合被测程序的代码设计结构来设计测试用例...

第三次因为表达式输出过于复杂，肉眼实在无法判断是否正确，所以写了简单的python程序来判断求导是否正确：

from sympy import *

from sympy.abc import x

str = eval(input().replace("^", "**"))

deri = eval(input().replace("^", "**"))

print("str: ", str.diff(x).subs({x:100}).evalf())

print("deri: ", deri.subs({x:100}).evalf())

四、Applying Creational Pattern

工厂模式的好处

我们以类Sample为例，如果我们要创建Sample的实例对象:

Sample sample=new Sample();

可是，实际情况是，通常我们都要在创建sample实例时做点初始化的工作,比如赋值查询数据库等。

首先，我们想到的是，可以使用Sample的构造函数，这样生成实例就写成:

Sample sample=new Sample(参数);

但是，如果创建sample实例时所做的初始化工作不是像赋值这样简单的事，可能是很长一段代码，如果也写入构造函数中，那你的代码很难看了（就需要Refactor重构）。

为什么说代码很难看，初学者可能没有这种感觉，我们分析如下，初始化工作如果是很长一段代码，说明要做的工作很多，将很多工作装入一个方法中，相当于将很多鸡蛋放在一个篮子里，是很危险的，这也是有悖于Java面向对象的原则，面向对象的封装(Encapsulation)和分派(Delegation)告诉我们，尽量将长的代码分派“切割”成每段，将每段再“封装”起来(减少段和段之间耦合联系性)，这样，就会将风险分散，以后如果需要修改，只要更改每段，不会再发生牵一动百的事情。（参考：百度百科工厂模式）

一开始我是把所有的构造都写在了构造函数里，但这样将对象的创建和使用放在一起，非常不利于封装和分派，不符合设计模式的开闭原则（对扩展开放，对修改关闭。在程序需要进行拓展的时候，不能去修改原有的代码）。

于是我构造工厂类进行重构，将项的构造分离出来：

构造工厂类前：

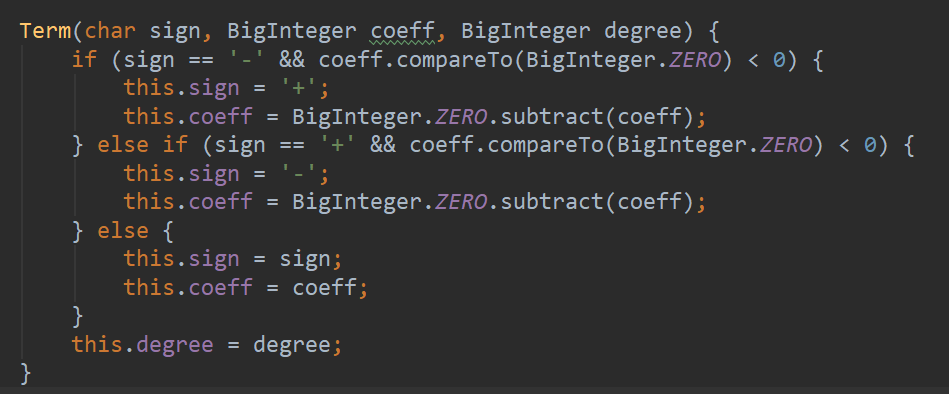
构造工厂类后：

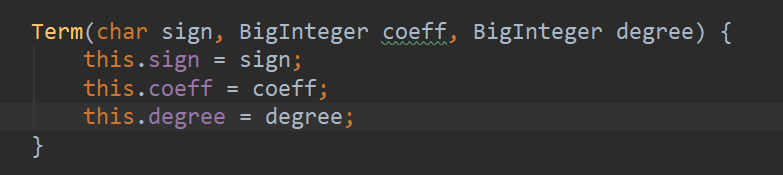
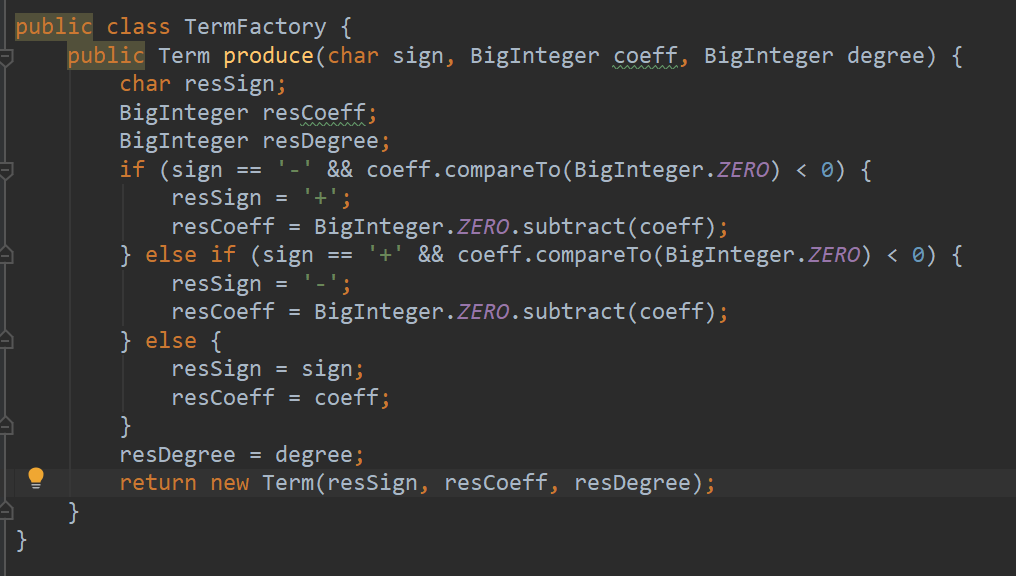至于更多创建型模式，如：工厂方法模式、抽象工厂模式、单例模式、建造者模式、原型模式等，目前还没有太深的理解。需要在以后实践中不断重构来加深认识。