算法复习——背包dp

1.01背包

二维递推式子：

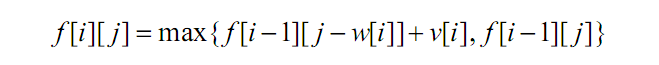
代码：

  for (i=;i<=n;i++)
    for (x=m;x>=;x--)
         if (x>=w[i]) f[i][x]=max(f[i-][x-w[i]]+c[i],f[i-][x]);
         else f[i][x]=f[i-][x];

  printf("%d",f[n][m]);              // f(n，m)为最优解
  return ;

然而有时候，由于容量或者物品数过多可能导致用二维数组可能超空间，此时可以考虑一维的优化

用f[i]表示当使用了i的容量后最多可以装多少价值的物品，我们可以推出以下代码：

for(int i=;i<=n;i++)
    for(int j=m;j>;j--)
      if(w[i]<=j)  f[j]=max(f[j],f[j-w[i]]+c[i]);

和上面比两段代码时间复杂度相同，而空间复杂度则得变小了许多，注意枚举容量j的时候一定要按倒叙枚举，顺序枚举可能出现重复拿同一物品的情况···也就是完全背包

注意有些时候,背包的限制条件有时候不只一个···比如说出了重量以外，可能加入体积等额外限制,这时我们只需再多加入一维.dp[i][j]表示使用重量为i，体积为j时的最大价值,代码如下：

for (i=;i<=n;i++)
        for (j=vv;j>=v[i];j--)
            for (k=gg;k>=g[i];k--)
               if (f[j][k]<f[j-v[i]][k-g[i]]+t[i])
                   f[j][k]=f[j-v[i]][k-g[i]]+t[i];

一道例题：

01背包的思路，虽然具体实现可能有点差别

可以用二维数组,dp[i][j]表示拿到第i个垃圾（还未决定是否吃或者堆）时，还有j的生命值，此时已经到达的最高高度，为了保证每次枚举的状态都是存在的。我用二维时是用前面的来更新后面的···和背包的有所不同：dp[i][j]+h[i]=dp[i+1][j-w[i+1]],dp[i][j]=dp[i+1][j+f[i]-w[i+1]],w表示的是拿到第i袋垃圾时需要等待的时间,注意转移时需要满足的条件（就是j始终要>=0）

代码：

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<ctime>
#include<cctype>
#include<cstring>
#include<string>
#include<algorithm>
using namespace std;
int d,g,dp[][];
bool jud[][],flag=false;
struct node
{
  int t,f,h,w;
}r[];
inline bool cmp(node a,node b)
{
  return a.t<b.t;
}
int main()
{
  memset(dp,-/,sizeof(dp));
  memset(jud,false,sizeof(jud));
  dp[][]=;jud[][]=true;
  scanf("%d%d",&d,&g);
  for(int i=;i<=g;i++)
  {
    scanf("%d%d%d",&r[i].t,&r[i].f,&r[i].h);
  }
  sort(r+,r+g+,cmp);
  for(int i=;i<=g;i++)
  {
    r[i].w=r[i].t-r[i-].t;
  }
  for(int i=;i<=g;i++)
  {
    for(int j=;j>=;j--)
    {
      if(jud[i][j])
      {
        if(dp[i][j]+r[i].h>=d)
        {
        if(r[i].t==)cout<<r[i+].t<<endl;
          else cout<<r[i].t<<endl;
          return ;
        }
        if(j-r[i+].w>=)  dp[i+][j-r[i+].w]=max(dp[i+][j-r[i+].w],dp[i][j]+r[i].h),jud[i+][j-r[i+].w]=true;
        if(j+r[i].f-r[i+].w>=)  dp[i+][j+r[i].f-r[i+].w]=max(dp[i+][j+r[i].f-r[i+].w],dp[i][j]),jud[i+][j+r[i].f-r[i+].w]=true;//注意这里的两个if判断
      }
    }
  }
  loop:
  int k=;
  for(int i=;i<=g;i++)
  {
    if(k<r[i].t)
    {
      printf("%d",k);
      return ;
    }
    k=k+r[i].f;
  }
  printf("%d",k);
}

然而01背包用一位数组往往代码量要小很多····并且思路也更简洁，我们用dp[i]表示在将高度堆到i时候的总共最长能活多久，对于物品j,dp[h[j]+i]=max{dp[h[j]+i],dp[i]},同时dp[i]+=f[j]

代码如下(引用YihAN_Z)：

#include <cstdio>
#include <algorithm>
#define max(a,b) (a>b?a:b)
using namespace std;
struct garbage{
    int e,h,t;//energy,height,time
    bool operator < (const garbage &x) const{return x.t>t;}
}a[];
int m,n,f[];
int main(){
    f[]=;
    scanf("%d%d",&m,&n);
    for(int i=;i<=n;i++) scanf("%d%d%d",&a[i].t,&a[i].e,&a[i].h);
    sort(a+,a++n);
    for(int j=;j<=n;j++)
        for(int i=m;i>=;i--){
            if(a[j].t>f[i]) continue;
            if(i+a[j].h>=m) {
                printf("%d\n",a[j].t);
                return ;
            }
            f[i+a[j].h]=max(f[i+a[j].h],f[i]);
            f[i]+=a[j].e;
        }
    printf("%d\n",f[]);
    return ;
}

2.完全背包：

二维递推式子：

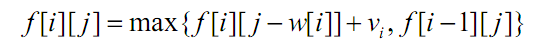
代码：

for(int i=;i<=n;i++)
    for(int j=;j<=m;j++)
    {
      if(w[i]<=j)
        dp[i][j]=max(dp[i-][j],dp[i][j-w[i]]+c[i]);
      else
        dp[i][j]=dp[i-][j];
    }

同样的可以搞搞一维优化，只是如上面01背包时说的一样，这时就要按顺序枚举了：

for(int i=1;i<=n;i++)
    for(int j=1;j<=m;j++)
      if(w[i]<=j)  f[j]=max(f[j],f[j-w[i]]+c[i]);

例题表示我找到不多而且都很裸····大家网上搜一搜吧···

3.多重背包

二维递推式子：

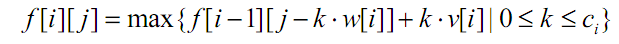
代码：

for int i=;i<=n;i++)
    for(int j=;j<=m;j++)
    {
      for(int k=;k<=c[i];k++)
        if(j>=k*w[i])  dp[i][j]=max(dp[i][j],dp[i-][j-k*w[i]]+k*v[i]);
      dp[i][j]=max(dp[i][j],dp[i-][j]);
    }

多重背包也能简单地用一维优化,注意和01背包一样是倒序枚举。注意要先枚举容量再枚举数量

for(int i=;i<=n;i++)
    for(int j=m;j>=;j--)
    {
      for(int k=;k<=c[i];k++)
        if(j>=k*w[i]) dp[j]=max(dp[j],dp[j-w[i]*k]+v[i]*k);
    }

然而不难发现，其实多重背包的时间复杂度是远大于前面所提到的两个背包的,其实针对多重背包还有一种优化时间的方式，会在今后的dp优化提到

来一道例题吧：

hdu1059

Problem Description

Marsha and Bill own a collection of marbles. They want to split the collection among themselves so that both receive an equal share of the marbles. This would be easy if all the marbles had the same value, because then they could just split the collection in half. But unfortunately, some of the marbles are larger, or more beautiful than others. So, Marsha and Bill start by assigning a value, a natural number between one and six, to each marble. Now they want to divide the marbles so that each of them gets the same total value. 
Unfortunately, they realize that it might be impossible to divide the marbles in this way (even if the total value of all marbles is even). For example, if there are one marble of value 1, one of value 3 and two of value 4, then they cannot be split into sets of equal value. So, they ask you to write a program that checks whether there is a fair partition of the marbles.

Input

Each line in the input describes one collection of marbles to be divided. The lines consist of six non-negative integers n1, n2, ..., n6, where ni is the number of marbles of value i. So, the example from above would be described by the input-line ``1 0 1 2 0 0''. The maximum total number of marbles will be 20000.

The last line of the input file will be ``0 0 0 0 0 0''; do not process this line.

Output

For each colletcion, output ``Collection #k:'', where k is the number of the test case, and then either ``Can be divided.'' or ``Can't be divided.''.

Output a blank line after each test case.

Sample Input

1 0 1 2 0 0 1 0 0 0 1 1 0 0 0 0 0 0

Sample Output

Collection #1: Can't be divided. Collection #2: Can be divided.

 

 

题解：

算出数字的总和,如果是奇数直接输出不行··如果是偶数问题转化为是否能拿出几个数使其总和为sum/2,从而转化成了多重背包问题···

注意这个dp要剪枝不然要T,这个剪枝也是很奇妙啊···具体看代码把，这里引用cdsszjj的解释，%%%：

起初以为多重背包枚举状态会超时，但借鉴了别人的剪枝后就过了， 
将价值从大到小枚举，那对于两个价值a1,a2(a1小于a2)，当枚举同一级别的弹珠k时，若(a2-a1)%k==0,那a1+x个k可能会等于a2+y个k，而此后a1+z个k（z>x）就一定会等于a2+(y+(z-x))个k。若倒着枚举就可以break剪枝了。

代码：

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<ctime>
#include<cctype>
#include<cstring>
#include<string>
#include<algorithm>
using namespace std;
int sum,num[],f[];
int main()
{
  //freopen("a.in","r",stdin);
  for(int t=;;t++)
  {
    sum=;memset(f,,sizeof(f));
    for(int i=;i<=;i++)
      scanf("%d",&num[i]),sum+=num[i]*i;
    if(!sum)  break;
    printf("Collection #%d:\n",t);
    if(sum%==) {printf("Can't be divided.\n");putchar('\n');continue;}
    sum/=;f[]=;int tot=;
    for(int i=;i<=;i++)
    {
      if(!num[i])  continue;
      for(int j=tot;j>=;j--)
      {
        if(f[j])
          for(int k=;k<=num[i];k++)
            if(j+i*k<=sum)
            {
              if(f[j+i*k]&&k)  break;
              f[j+i*k]=true;
            }
      }
      tot=max(sum,tot+num[i]*i);
    }
    if(f[sum]) printf("Can be divided.\n");
    else printf("Can't be divided.\n");putchar('\n');
  }
  return ;
}
 

最后再来一道混合背包的问题：

通过分析不难得出,这是一道完全背包+多重背包+二维费用的背包问题····,上面这3种情况都讲过，现在只用将其混合起来即可······能做对这道题背包问题的基础就差不多掌握了···

同时这道题也充分体现了一维优化的空间优越性·····

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<ctime>
#include<cctype>
#include<cstring>
#include<string>
#include<algorithm>
using namespace std;
const int N=;
const int M=;
int v[N],w1[N],w2[N],c[N],dp[M][M],n,m1,m2;
int main()
{
  scanf("%d%d%d",&n,&m1,&m2);
  for(int i=;i<=n;i++)
    scanf("%d%d%d%d",&w1[i],&w2[i],&c[i],&v[i]);
  for(int i=;i<=n;i++)
  {
    if(!c[i])
      for(int j=w1[i];j<=m1;j++)
        for(int k=w2[i];k<=m2;k++)
          dp[j][k]=max(dp[j][k],dp[j-w1[i]][k-w2[i]]+v[i]);
    else
      for(int j=m1;j>=w1[i];j--)
        for(int k=m2;k>=w2[i];k--)
          for(int l=;l<=c[i];l++)
            if(j>=w1[i]*l&&k>=w2[i]*l)
              dp[j][k]=max(dp[j][k],dp[j-w1[i]*l][k-w2[i]*l]+v[i]*l);
  }
  cout<<dp[m1][m2]<<endl;
  return ;
}

最后再总结一下背包dp类的问题吧···其实背包问题并不复杂，充分熟悉每一种背包的特性，每次分析出问题的背包组成类型（如上题），然后配上相应的思想和代码即可