[BZOJ5286][洛谷P4425][HNOI2018]转盘（线段树）

5286: [Hnoi2018]转盘

Time Limit: 20 Sec Memory Limit: 512 MB
Submit: 15 Solved: 11
[Submit][Status][Discuss]

Description

一次小G和小H准备去聚餐，但是由于太麻烦了于是题面简化如下：

一个转盘上有摆成一圈的n 个物品（编号1~n ），其中的i 个物品会在T_i时刻出现。

在0时刻时，小G可以任选n 个物品中的一个，我们将其编号为s_0 。并且如果i时刻选择了物品s_i ，那么i+1 时刻可以继续选择当前物品或选择下一个物品。当s_i为n 时，下一个物品为物品1 ，否则为物品s_i+1 。

在每一时刻（包括0时刻），如果小G选择的物品已经出现了，那么小G将会标记它。小H想知道，在物品选择的最优策略下，小G什么时候能标记所有物品？

但麻烦的是，物品的出现时间会不时修改。我们将其描述为m 次修改，每次修改将改变其中一个物品的出现时间。每次修改后，你也需求出当前局面的答案。对于其中部分测试点，小H还追加了强制在线的要求。

Input

第一行三个非负整数n 、m 、p ，代表一共有n 个物品，m 次修改。p 只有0或1两种取值，强制在线时p 为1，否则p 为0.

接下来一行，有n 个非负整数，第i个数T_i代表物品i的出现时间。

接下来m行，每行两个非负整数x 、y ，代表一次修改及询问。修改方式如下：

（1）如果p=0 ，则表示物品x 的出现时间T_x 修改为y 。

（2）如果p=1 ，在先将x 和y 分别异或LastAns，得到x'和y′，然后将物品x' 的出现时间T_x' 修改为y′ 。其中的LastAns 是前一个询问的结果；特别的，第一次修改时LastAns为初始局面的答案。

保证输入合法。

Output

第一行一个整数，代表初始局面的答案。

接下来m 行每行一个整数，分别代表每次修改后的答案。

Sample Input

Sample Output

HINT

Source

鸣谢hu1029282594上传

分析：

bzoj没有题面，自己手动整理题面好麻烦。。

题意就是：有一个圈，找一个点作为起点，可以停顿或者往前走，每个点物品都有个出现时间，当我们到达这个点且物品存在就可以拿走他，问所有物品都被拿走需要的最少时间

可以根据神奇的推论：

选择一个点s，最优答案一定是停顿一会儿，之后不停歇的走完一圈。因为是圈，处理时，将Ti倍长。

那么答案就变成了

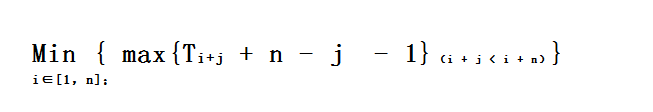
又因为Ti == Ti + n

所以

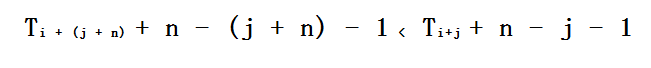
又由于里层循环是取max，所以答案可以变为

记录 Ai = Ti - i

那么答案变为了

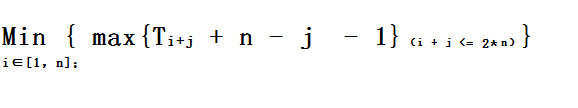
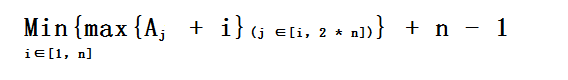
此时只需要用线段树维护一下就好了，首先维护每段区间Ai的最大值，

然后在push时，对于i ∈[l，mid]，找到最小的 i + Aj 并储存下来，这个O（logn）递归可以做到。

总复杂度O（nlogn^2 + mlogn^2）

AC代码：

# include <iostream>
# include <cstdio>
# include <cstring>
using namespace std;
const int N = 2e5 + ;
int T[N],A[N],n,m,k;
struct Seg{
    int mx[N << ],mi[N << ];
    int Query(int l,int r,int rt,int bac)
    {
        if(l == r)return l + max(mx[rt],bac);
        int mid = l + r >> ;
        if(mx[rt <<  | ] < bac)
        return min(Query(l,mid,rt << ,bac),mid +  + bac);
        return min(mi[rt],Query(mid + ,r,rt <<  | ,bac));
    }
    void push(int l,int r,int rt)
    {
        mi[rt] = Query(l,l + r >> ,rt << ,mx[rt <<  | ]);
        mx[rt] = max(mx[rt << ],mx[rt <<  | ]);
    }
    void build(int l,int r,int rt)
    {
        if(l == r){mx[rt] = A[l];mi[rt] = T[l];return;}
        int mid = l + r >> ;
        build(l,mid,rt << );
        build(mid + ,r,rt <<  | );
        push(l,r,rt);
    }
    void updata(int L,int l,int r,int rt)
    {
        if(l == r){mx[rt] = A[l];mi[rt] = T[l];return;}
        int mid = l + r >> ;
        if(L <= mid)updata(L,l,mid,rt << );
        else updata(L,mid + ,r,rt <<  | );
        push(l,r,rt);
    }
}B;
int main()
{
  scanf("%d %d %d",&n,&m,&k);
  for(int i = ;i <= n;i++)
  {
      scanf("%d",&T[i]);T[i + n] = T[i];
      A[i] = T[i] - i;A[i + n] = A[i] - n;
  }
  B.build(,n << ,);
  int las,x,y;printf("%d\n",las = B.mi[] + n - );
  while(m--)
  {
      scanf("%d %d",&x,&y);x ^= k * las,y ^= k * las;
      T[x] = T[x + n] = y;A[x] = T[x] - x;A[x + n] = A[x] - n;
      B.updata(x,,n << ,);B.updata(x + n,,n << ,);
      printf("%d\n",las = B.mi[] + n - );
  }
}