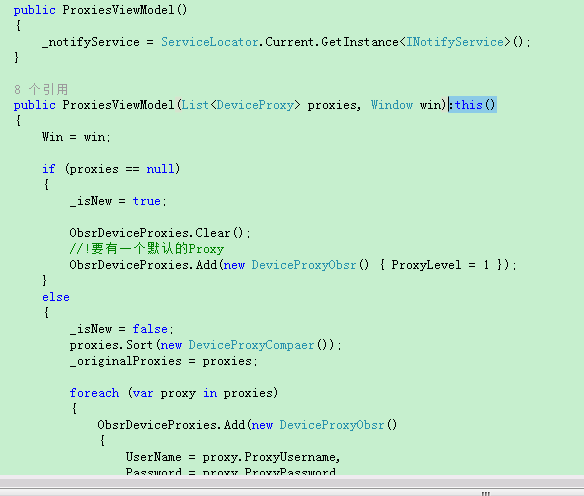
构造方法后面带:this()
可以这么理解,有参数的构造函数需要执行无参构造函数中的代码,为了省去重复代码的编写,所以就继承了,先执行没参数的那个构造函数。
在this上“转到定义”(F12)就到第一个构造函数上去了.
构造方法后面带:this()的更多相关文章
- 写java代码有感。。。构造方法最好带着,
(一) 小结:具体我最大的担心,害怕就是方法调用的时候,new对象之后,赋值,是在new后面的括号里实现,还是在 对象.方法名()这样的.当然带参数的构造方法,调用时本身就直接调用,普通方法,选后者. ...
- 附录A培训实习生-面向对象基础构造方法和带参数的构造方法(2)
构造方法,又叫构造函数,其实就是对类进行实例化.构造方法与类同名,无返回值,也不需要void,在new时候调用.也就是说,就是调用构造方法的时候. 所有类都有构造方法,如果你不编码则系统默认生成空的的 ...
- 通过继承Rect类编写一个具有确定位置的矩形类PlainRect,其确定位置用 矩形的左上角坐标来标识,包含: 添加两个属性:矩形左上角坐标startX和startY。 两个构造方法: 带4个参数的构造方法,用于对startX、startY、width和height属性 初始化; 不带参数的构造方法,将矩形初始化为左上角坐标、长和宽都为0 的矩形; 添加一个方法: 判断某个点是否在矩形内部的方法
package b; public class Rect { Double width; Double height; public Double getWidth() { return width; ...
- php面向对象编程之构造方法__construct()
php中构造方法是对象创建完成后第一个被对象自动调用的方法.在每个类中都有一个构造方法,如果没有显示地声明它,那么类中都会默认存在一个没有参数且内容为空的构造方法. 构造方法的作用 通常构造方法被用来 ...
- Java基础---基础加强---增强for循环、自动拆装箱及享元、枚举的作用、实现带有构造方法、透彻分析反射的基础_Class类、成员变量的反射、数组参数的成员方法进行反射、数组的反射应用
在perference 加content Assist 可以设置快捷键 透视图与视图 透视图:Debug和java主窗口 视图:每一个小窗口就是视图 高版本的java可运行低版本的java版本 常见的 ...
- c#核心基础--类的构造方法
一.构造方法 类的构造方法是类的成员方法的一种,它的作用是对类中的成员进行初始化操作.类的构造方法分为: 1.静态构造方法 2.实例构造方法 3.私有构造方法 1.静态构造方法 类的静态构造方法是类的 ...
- java基础知识 构造方法
在java里面,构造方法也就是构造函数 构造函数=构造方法;构造方法是一种特殊的方法,具有以下特点.(1)构造方法的方法名必须与类名相同.(2)构造方法没有返回类型,也不能定义为void,在方法名前面 ...
- java构造方法之我见
java中构造方法是作为除了成员方法之外的一种特殊方法,方法名与类名相同.一般类中如果没有明确定义构造方法时,编译器默认为无参构造方法.当我们调用new方法创建对象就是通过构造方法完成的.因此,当有对 ...
- JavaSE入门学习23:Java面向对象之构造方法
学了JavaSE面向对象这一部分,也该对构造方法做一个总结了. 一构造方法 在多数情况下,初始化一个对象的终于步骤是去调用这个对象的构造方法. 构造方法负责对象的初始化工作,为 实例变量赋予合适的初始 ...
随机推荐
- [python学习篇][廖雪峰][4]函数--reduce
reduce的用法.reduce把一个函数作用在一个序列[x1, x2, x3...]上,这个函数必须接收两个参数,reduce把结果继续和序列的下一个元素做累积计算,其效果就是: reduce(f, ...
- ubuntu14.04修改mysql默认编码
修改文件为/etc/mysql/my.cnf [client] default-character-set = utf8 (ps:client的设置没变) [mysqld] lower_case_ta ...
- 【Luogu】P3565HOT-Hotels(树形DP)
题目链接 水了半个月之后Fd终于开始做题啦! 然后成功的发现自己什么都不会了 树形DP,既然是三个点两两距离相等那一定得有个中心点吧,枚举那个中心点,然后暴力DFS,根据乘法原理算. 乘法原理就是我一 ...
- Java学习——个人错误集(1)
[General] 1.构造函数没有返回值,连void也没有. [多态Polymorphism]
- css的部分应用示例
CSS :层叠样式表,Cascading Style Sheets.CSS不仅可以静态地修饰网页,还可以配合各种脚本语言动态地对网页各元素进行格式化. 1 vertical-align 在图片与文字对 ...
- Springboot 版本+ jdk 版本 + Maven 版本的匹配
Spring boot 版本 Spring Framework jdk 版本 maven 版本 1.2.0 版本之前 6 3.0 1.2.0 4.1.3+ 6 3.2+ 1.2.1 4.1.3+ 7 ...
- 几个类和Table的方法
public class TableHelper { public static DataTable CreateTableFromClass(Type t) { DataTable dt = new ...
- linux 下高精度时间
今天在公司代码中看到了使用select函数的超时功能作定时器的用法,便整理了如下几个Linux下的微秒级别的定时器.在我的Ubutu10.10 双核环境中,编译通过. /* * @FileName: ...
- 快充 IC BQ25896 如何判斷 手機插著 adapter 充電器時,adapter Iout 大於限制,adapter Vout 小於 限制,導致 battery 不但沒充電且還需放電。
若電池在 放電時,ICHGR 為0. 若電池在 充電時,ICHGR有變化. 下面有寫到 charge current 所以不是 discharge current 狀況: ...
- os.system() 和 os.popen()
1.os.popen(command[, mode[, bufsize]]) os.system(command) 2.os.popen() 功能强于os.system() , os.popen() ...
