P1308-道路修建 （noi 2011）

题目描述

在 W 星球上有 n 个国家。为了各自国家的经济发展，他们决定在各个国家 之间建设双向道路使得国家之间连通。但是每个国家的国王都很吝啬，他们只愿 意修建恰好 n – 1 条双向道路。 每条道路的修建都要付出一定的费用，这个费用等于道路长度乘以道路两端 的国家个数之差的绝对值。例如，在下图中，虚线所示道路两端分别有 2 个、4 个国家，如果该道路长度为 1，则费用为 1×|2 – 4|=2。图中圆圈里的数字表示国 家的编号。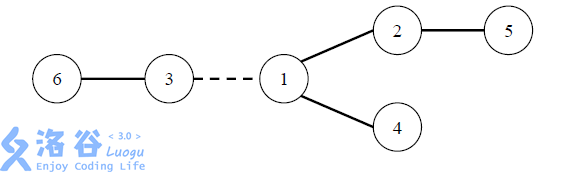 

由于国家的数量十分庞大，道路的建造方案有很多种，同时每种方案的修建 费用难以用人工计算，国王们决定找人设计一个软件，对于给定的建造方案，计 算出所需要的费用。请你帮助国王们设计一个这样的软件。

输入输出格式

输入格式：

输入的第一行包含一个整数 n，表示 W 星球上的国家的数量，国家从 1 到 n 编号。 接下来 n – 1 行描述道路建设情况，其中第 i 行包含三个整数 ai、bi和 ci，表 示第 i 条双向道路修建在 ai与 bi两个国家之间，长度为 ci。

输出格式：

输出一个整数，表示修建所有道路所需要的总费用。

---

哇， noi ， 好怕怕，哎？好像有点水．．．

首先这是一棵树， size[i]表示以i为节点的子树的大小， 设一个点为i， 它的父亲节点为fa， 则显然两个点的相差的国家为(n - 2 * size[i]), 这样可以用bfs或dfs预处理出每个点子树的大小， 然后枚举每条边即可， 洛谷dfs就可以过， 本校oj需要bfs。。。

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;
const int INF = 0x3f3f3f3f;
const int MAXN = 1e6 + ;
//const int MAXM = 3e3 + 10;

template < typename T > inline void read(T &x) {
    x = ; T ff = , ch = getchar();
    while(!isdigit(ch)) {
        if(ch == '-') ff = -;
        ch = getchar();
    }
    while(isdigit(ch)) {
        x = (x << ) + (x << ) + (ch ^ );
        ch = getchar();
    }
    x *= ff;
}

template < typename T > inline void write(T x) {
    if(x < ) putchar('-'), x = -x;
    if(x > ) write(x / );
    putchar(x %  + '');
}

struct edge {
    int y, v, next;
}e[MAXN << ];
int n, size[MAXN], fa[MAXN];
int tot = , lin[MAXN];
int id[MAXN], ti = ;
ll ans;

inline void add(int xx, int yy, int vv) {
    e[++tot].y = yy;
    e[tot].v = vv;
    e[tot].next = lin[xx];
    lin[xx] = tot;
}

/*void DFS(int x) {
    size[x] = 1;
    for(int i = lin[x], y; i; i = e[i].next) {
        if(size[y = e[i].y]) continue;
        DFS(y);
        ans += (ll)abs(n - 2 * size[y]) * e[i].v;
        size[x] += size[y];
    }
}*/        

void BFS() {
    queue < int > q;
    q.push();
    while(!q.empty()) {
        int x = q.front(); q.pop();
        for(int i = lin[x], y; i; i = e[i].next) {
            if((y = e[i].y) != fa[x]) {
                fa[y] = x;
                q.push(y);
                id[++ti] = y;
            }
        }
    }
}                 

int main() {
//    freopen("1.in", "r", stdin);
    read(n);
    for(int i = ; i < n; ++i) {
        int x, y, v;
        read(x); read(y); read(v);
        add(x, y, v);
        add(y, x, v);
    }
    for(int i = ; i <= n; ++i)
        size[i] = ;
    BFS();
    for(int i = ti; i >= ; --i)
        size[fa[id[i]]] += size[id[i]];
    for(int i = ; i <= tot; i += ) {
        int x = e[i].y, y = e[i ^ ].y;
        int mi = min(size[x], size[y]);
        ans += (ll)abs(n -  * mi) * e[i].v;
    }
//    DFS(1);
    write(ans);
    return ;
}