【原创】洛谷 LUOGU P3366 【模板】最小生成树

P3366 【模板】最小生成树

题目描述

如题，给出一个无向图，求出最小生成树，如果该图不连通，则输出orz

输入输出格式

输入格式：

第一行包含两个整数N、M，表示该图共有N个结点和M条无向边。（N<=5000，M<=200000）

接下来M行每行包含三个整数Xi、Yi、Zi，表示有一条长度为Zi的无向边连接结点Xi、Yi

输出格式：

输出包含一个数，即最小生成树的各边的长度之和；如果该图不连通则输出orz

输入输出样例

输入样例#1：

4 5
1 2 2
1 3 2
1 4 3
2 3 4
3 4 3

输出样例#1：

7

说明

时空限制：1000ms,128M

数据规模：

对于20%的数据：N<=5，M<=20

对于40%的数据：N<=50，M<=2500

对于70%的数据：N<=500，M<=10000

对于100%的数据：N<=5000，M<=200000

样例解释：

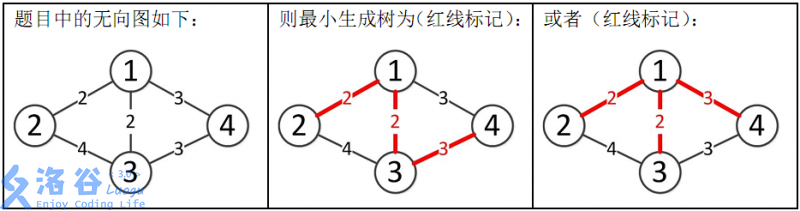
所以最小生成树的总边权为2+2+3=7

 

 

练习最小生成树，用了mhy12345大神的风格写了Kruskal算法。

Kruskal的思路：（贪心）

　　将边集按权值排序，

　　用并查集维护，从小到大连边，

　　这样就能保证所有环的最大边一定不被连上，

　　计算已加节点cnt，当cnt==n-1时即生成完毕。

　　若边集遍历完但cnt<n-1则图不连通。

　　时间复杂度即为排序复杂度，一般为O(ElogE)。

代码如下：

 // LUOGU 3366 【模板】最小生成树
 // 2017.7.21 12:55
 #include<cstdio>
 #include<cstdlib>
 #include<cstring>
 #include<iostream>
 #include<string>
 #include<algorithm>
 #define MAXV 5010
 #define MAXE 200010
 using namespace std;
 struct tEdge{
     int u,v,w;
 }E[MAXE];
 int n,m,ans=,cnt=;
 int uf[MAXV];
 bool cmp(const tEdge E1,const tEdge E2){
     return E1.w<E2.w;
 }
 int getfather(int v){
     return (uf[v]==v)?v:uf[v]=getfather(uf[v]);
 }
 bool Union(tEdge E){
     if(getfather(E.u)!=getfather(E.v)){
         uf[getfather(E.u)]=getfather(E.v);
         return ;
     }
     return ;
 }
 int main(){
     scanf("%d%d",&n,&m);
     for(int i=;i<=m;i++)
         scanf("%d%d%d",&E[i].u,&E[i].v,&E[i].w);
     sort(E+,E+m+,cmp);
     for(int i=;i<=n;i++)uf[i]=i;
     for(int i=;i<=m;i++)
         if(Union(E[i])){
             ans+=E[i].w,cnt++;
             if(cnt==n-)break;
         }
     if(cnt==n-)printf("%d\n",ans);
     else printf("orz\n");
     return ;
 }