POJ1979(Red and Black)--FloodFill

题目在这里

题目意思是这样的，一个人起始位置在    '@'  处，他在途中能到达的地方为 ' .  '     而  '#' 是障碍物，他不能到达。

问途中他所有能到达的   '.'的数量是多少 ？？当然，他自己本身也算一个能到达的点。

其中两个样例的结果是这样的走出来的，这是"显而易见"的,哈哈～当然，当图很大的时候，数起来就能费事了。

所用的这个方法叫做FlooFill(洪水覆盖)，从它名字来看就是个很暴力直接的方法，只要我能到的地方，我都用水把你淹没了。可以联想一下，在田地里用水渠灌溉田地时，只要你把要灌溉的地方挖好水道，最后，只要打开总的水闸开关，那么所有你想灌溉的田里最后都会有水进去。那个水闸就是这里的@点了。

再看百度百科的解释

画图的填充就是这么来的，通俗的来说，无孔不入。所以，我把这个题看做画图填充，用这个方法做肯定不会错了。

由于存在计数问题，所以稍微处理下，首先将每个'.'看做是oldColer，即我还没填充到它，后面，就对所有我没填充到的点(颜色为oldColor的)并且是我能到达的点进行填充(一定是能到达的才能)，把它变为(newColor1)，每成功的涂色一次，就把计数加1,这样，就不存在计数问题了。

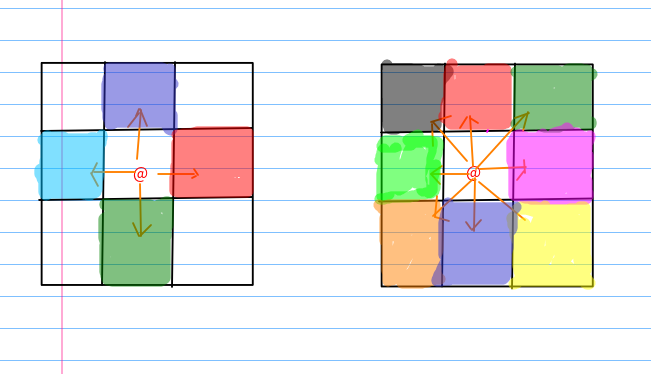
再对每个格子进行扩展填充时，可以有这上述两种填充方法（有点尴尬，我画图竟然没找到颜色填充。。。。）

然后每扩充一个格子，就再以那个格子为起点，继续扩充，即递归的填充，直到所有的格子都被填完。

 /*************************************************************************
     > File Name: poj1979.cpp
     > Author: YeGuoSheng
     > Description:
     man at @，Q:how many points('.') he can arrive
     #:can not be arrived
     > Created Time: 2019年07月23日 星期二 16时32分10秒
  ************************************************************************/
 #include<iostream>
 #include<stdio.h>
 #include<cstring>
 #include<cmath>
 #include<vector>
 #include<stack>
 #include<map>
 #include<set>
 #include<list>
 #include<queue>
 #include<string>
 #include<algorithm>
 #include<iomanip>
 using namespace std;
 const int maxn = ;
 char g[maxn][maxn];//cin matrix
 int G[maxn][maxn];//color the g ;
 int n,m;//row ,col
 int ans = ;
 int startx,starty;

 int GetColor(int x,int y)
 {
     return G[x][y];
 }

 void SetColor(int x,int y,int newColor)//change color 0  to 1
 {
     G[x][y] = newColor;
     ans++;//result ++
 }

 void FloodFill(int x,int y,int oldColor,int newColor)
 {
     if( x>=  && x< n && y >= && y < m && GetColor(x,y) == oldColor)
     {//Current position legal ,and color is oldColor => no access
         SetColor(x,y,);//change color
         FloodFill(x-,y,oldColor,newColor);//Flood covers the upper right and lower left four points
         FloodFill(x,y+,oldColor,newColor);
         FloodFill(x+,y,oldColor,newColor);
         FloodFill(x,y-,oldColor,newColor);
     }
 }

 int main()
 {
     while(scanf("%d%d",&m,&n)&& n !=  && m!=)
     {
         ans = ;
         memset(G,,sizeof(G));
         memset(g,,sizeof(g));
         for(int i = ;i< n;i++)
         {
             for(int j = ;j < m;j++)
             {
                 cin>>g[i][j];
                 if(g[i][j]=='.')
                     G[i][j] = ;//old color
                 if(g[i][j]=='#')
                     G[i][j] = ;//new color && can not be covered
                 if(g[i][j]== '@')
                 {
                     G[i][j] = ;//old color
                     startx = i;
                     starty = j;
                 }
             }
         }
         FloodFill(startx,starty,,);
         cout<<ans<<endl;
     }
     return ;
 }