机器学习第一章——NFL的个人理解

第一篇博客，想给自己的学习加深记忆。看到书中第一个公式时，本来想直接看证明结果就好，然鹅。。。作者在备注上写：这里只用到一些非常基础的数学知识，只准备读第一章且有“数学恐惧”的读者可跳过。。。嘤嘤嘤，不服气，想弄明白一些。

就看到了知乎的这篇文章，算是我的启蒙文章了，感激。https://zhuanlan.zhihu.com/p/48493722

下面针对这篇文章加入自己的理解。

没有免费午餐定理是说无论两种算法  多聪明、  多笨拙，它们的期望性能竟然相同。

（1）期望性能

期望也叫均值：可以表述为有一种内在的动力趋于某种东西。简单解释：

在概率论和统计学中，一个离散性随机变量的期望值（或数学期望、或均值，亦简称期望，物理学中称为期待值）是试验中每次可能的结果乘以其结果概率的总和。换句话说，期望值像是随机试验在同样的机会下重复多次，所有那些可能状态平均的结果，便基本上等同“期望值”所期望的数。需要注意的是，期望值并不一定等同于常识中的“期望”——“期望值”也许与每一个结果都不相等。（换句话说，期望值是该变量输出值的平均数。期望值并不一定包含于变量的输出值集合里。）

例如，掷一枚公平的六面骰子，其每次“点数”的期望值是3.5，计算如下：

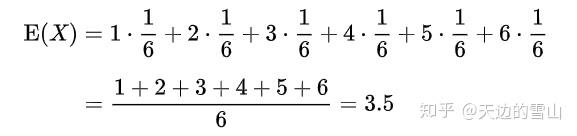
不过如上所说明的，3.5虽是“点数”的期望值，但却不属于可能结果中的任一个，没有可能掷出此点数。

（2）算法假设

NFL定理的前提是：所有问题出现的机会相同、或者说所有的问题同等重要。

没有免费的午餐定理(No Free Lunch Theorem),这个定理说明，若学习算法  ，在某些问题上比学习算法  要好， 那么必然存在另一些问题， 在这些问题中  比  表现更好。

（以下类比：La和Lb就像是两家父母，La的父母教育出来的孩子学习很好，但是Lb的父母教育出来的孩子自理能力很强）

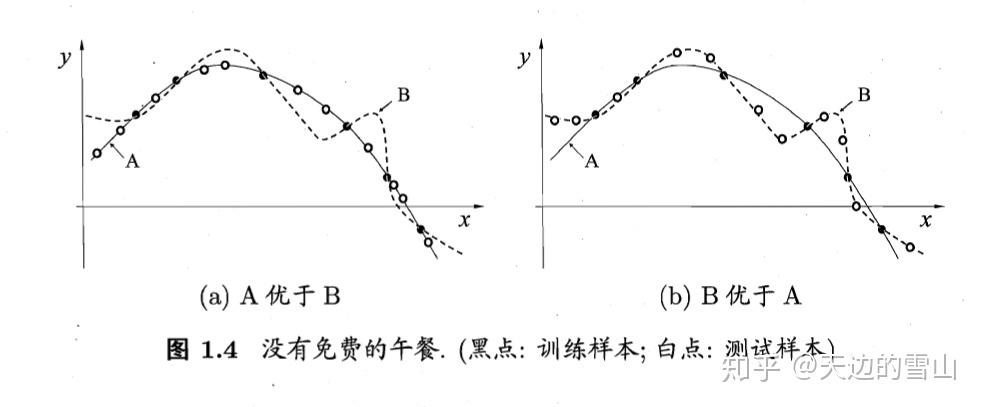
泛化能力就是：现在让两家父母用自己原来教育孩子的方法去培养其他的孩子

这里说的表现好就是前面所说的泛化能力更强。然后出现了下面这个公式

令人生畏的长公式，不过我们来依次解读它。

X : 样本空间，什么是样本空间呢?就是你的样本的属性张成的空间，书的前文有介绍

还是以他书中的西瓜来举例吧:

西瓜的属性和每个属性的取值是

色泽= 青绿||乌黑||浅白 x= 0 || 1 || 2

根蒂= 蜷缩||稍蜷||硬挺 y= 0 || 1 || 2

敲声= 浊响||沉闷||清脆 z= 0 || 1 || 2

你把色泽、根蒂、敲声想想成x，y，z轴。取值的范围都是0,1,2。怎么样，是不是像一个正方体的三维空间，当然属性可能有多种，那就上升到多维空间去了，不好想像了。

H:假设空间，什么是假设空间呢?

什么是假设呢，前面说也叫学得模型，这里我们不搞那些概念。请看这篇博主的文章http://blog.csdn.net/VictoriaW/article/details/77686168，看完应该就能理解假设空间和版本空间）

假设空间就是指La父母，可能把孩子培养成警察、程序员、宇航员、服务员、白富美、傻白甜。。。这些组成假设空间

但是呢根据传统的定义，只有宇航员和程序员才可以成为祖国的栋梁，这里版本空间就是祖国的栋梁定义下的组成

 :学习算法，学习算法有其偏好性，对于相同的训练数据，不同的学习算法可以产生不同的假设，学得不同的模型，因此才会有那个学习算法对于具体问题更好的问题，这里这个没有免费的午餐定理要证明的就是:若对于某些问题算法  学得的模型更好，那么必然存在另一些问题，这里算法  学得的模型更好。这里的好坏在下文中使用算法对于所有样本的总误差表示（就是相同的孩子给不同的父母培养，可能产生不同的结果）

P(h|X,  ): 算法La基于训练数据X产生假设h的概率（就是La父母训练完自己的孩子成为警察之后，开始训练别的孩子（X）了，P就是别的孩子在La父母的训练下成为警察的概率）

这里我说一下自己的理解，既然是  基于X产生假设h的概率，那么就说明假设不止一个(你说这不是废话吗？上面都说有假设空间了，假设当然不止一个)，这里要注意的是这里的假设是一个映射，是y=h(x)，（这个孩子变成警察算不算祖国的栋梁）是基于数据X产生的对于学习目标(判断好瓜)的预测。因数据X不一样，所以可能产生不一样的假设h,既然假设假设有可能不一样，那么对每一种假设都有其对应的概率即P(h|X, )。而且所有假设h加起来的概率为1，这个不难理解，概率总和为1（不成为警察最后成为各种职业的人，加起来概率为1，因为每个孩子总要当一个啥）

f: 代表希望学得的真实目标函数，要注意这个函数也不是唯一的，而是存在一个函数空间，在这个空间中按某个概率分布，下文证明中采用的是均匀分布。（f就是指最后成为了是祖国的栋梁）

（训练集外误差：La父母开始上路变成职业培训父母了，Eote是他们没有成功把社会上的孩子变成警察的这一事件的期望）

首先看这个E,这个E是期望，expectation的意思，这个下标ote，是off-training error，即训练集外误差Eote(  |X,f )算法  学得的假设在训练集外的所有样本上的误差的期望

P(x): 对于这个，我的理解是样本空间中的每个样本的取得概率不同，什么意思呢？拿西瓜来说，(色泽=浅白，根蒂=硬挺，敲声=清脆)的西瓜可能比(色泽=浅白，根蒂=稍蜷，敲声=沉闷)的西瓜更多，取到的概率更大。所以有P(x)这个概率。

I(h(x)≠f(x))看前面的符号表把这个叫做指示函数，这个很好理解，就像if语句括号里的表达式一样，为真就=1,为假就=0。（假就是指成功变为警察，不需要考虑了，只考虑没成功的）（与孩子本身P(x)和La的训练能力P(h|X,La)有关）

P(h|X,  ): 前面说过了，再复习一下，算法  基于训练集X产生假设h的概率。

好了，公式的每一部分都说清楚了，来整体理解一下，这个公式就是说:

第一个求和符号:

 : 这里的这个对假设的求和其实我也不是很理解，我的理解主要是算法对于同一个训练集会产生不同的假设，每个假设有不同的概率。（除了警察也可以是其他的职业，各种）

第二个求和符号:

 ：对于样本空间中每一个训练集外的数据都进行右边的运算。(训练集外的孩子)

好了，公式的每一部分都说清楚了，来整体理解一下，这个公式就是说:

对于算法  产生的每一个不同的假设h,进行训练外样本的测试，然后测试不成功(因为求的是误差)指示函数就为1，并且两个概率相乘,最后所有的结果加起来，就是该算法在训练集外产生的误差。

然后下面考虑二分类问题，先要说明，对于我们想要求得的真实目标函数  可能不止一个，这个好理解，因为满足版本空间中的假设的函数都可以是真实目标函数，然后这些不同的  有着相同的概率(均匀分布),函数空间为{0,1}{0,1},那么有多少个这种函数呢?我们来看对于同一个样本的这个预测值，对于样本空间χ中的某个样本x，如果f1(x)=0，f2(x)=1, 那么这就是两个不同的真实目标函数，所以对于某个样本可以区分出两个真实目标函数，一共有|χ|个样本，所以一共有  个真实目标函数，这些真实目标函数是等可能分布的(均匀分布),所以对于某个假设h(x)如果h(x)=0那么就有  的可能与真实目标函数相等。

所以下面来看这个公式推导

（有2^|x|个1/2）概率求和为1,就是这么简单

经过这么一通推导后，发现得出期望的表达式中关于没有具体算法的，所以是算法无关的!

写给自己看的，不喜勿喷。