遍历二叉树 - 基于递归的DFS（前序，中序，后序）

上节中已经学会了如何构建一个二叉搜索数，这次来学习下树的打印-基于递归的DFS，那什么是DFS呢？

有个概念就行，而它又分为前序、中序、后序三种遍历方式，这个也是在面试中经常会被问到的，下面来具体学习下,用三种遍历方法来遍历上节中的二叉数：

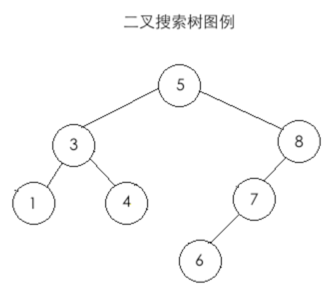
前序遍历：

那对于上面的二叉数用前序遍历，遍历过程如下：

1、先遍历根节点【5】

2、再遍历左子树:

需要注意的是：遍历左右子树时仍然采用前序遍历方法。所以如下：

　　a、先遍历根节点【3】

　　b、再遍历左子树，由于只有一个结点则直接打印【1】

　　c、再遍历右子树，由于只有一个结点则直接打印【4】

3、再遍历右子树：

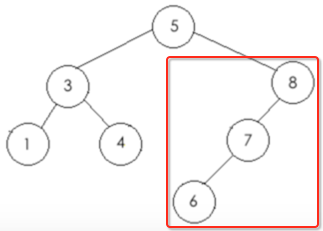
　　a、先遍历根节点【8】

　　b、再遍历左子树：

　　　　

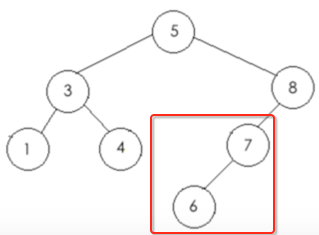
　　　　ba、先遍历根节点【7】

　　　　bb、再遍历左子树，由于只有一个结点则直接打印【6】

　　　　bc、再遍历右子树，由于木有右子树，递归返回。

　　c、再遍历右子树，由于木有右子树，递归返回。

至此整个前序遍历结束，结果如：【5】、【3】、【1】、【4】、【8】、【7】、【6】

下面看下代码具体实现，基于上节二叉搜索树的实现，增加一个遍历的方法，其它木变，直接上代码：

public class BinarySearchTree {
    TreeNode root = null;

    class TreeNode{
      int value;
      int position;
      TreeNode left = null, right = null;
      TreeNode(int value, int position){
        this.value = value;
        this.position = position;
      }
    }

    public void add(int value, int position){
      if(root == null){//生成一个根结点
        root = new TreeNode(value, position);
      } else {
        //生成叶子结点
        add(value, position, root);
      }
    }

    private void add(int value, int position, TreeNode node){
      if(node == null)
        throw new RuntimeException("treenode cannot be null");
      if(node.value == value)
        return; //ignore the duplicated value
      if(value < node.value){
        if(node.left == null){
          node.left = new TreeNode(value, position);
        }else{
          add(value, position, node.left);
        }
      }else{
        if(node.right == null){
          node.right = new TreeNode(value, position);
        }else{
          add(value, position, node.right);
        }
      }
    }

    //打印构建的二叉搜索树
    static void printTreeNode(TreeNode node) {
      if(node == null)
        return;
      System.out.println("node:" + node.value);
      if(node.left != null) {
        printTreeNode(node.left);
      }
      if(node.right != null) {
        printTreeNode(node.right);
      }
    }

    //搜索结点
    public int search(int value){
      return search(value, root);
    }

    private int search(int value, TreeNode node){
      if(node == null)
        return -1; //not found
      else if(value < node.value){
        System.out.println("Searching left");
        return search(value, node.left);
      }
      else if(value > node.value){
        System.out.println("Searching right");
        return search(value, node.right);
      }
      else
        return node.position;
    }

    //二叉树遍历
    public void travel(){
      travel(root);
    }
    public void travel(TreeNode node){
      if(node == null)
        return;
      System.out.println(" " + node.value);
      travel(node.left);
      travel(node.right);
    }

    public static void main(String[] args) {
      BinarySearchTree bst = new BinarySearchTree();
      int a[] = { 5, 8, 3, 4, 1, 7, 6};
      for(int i = 0; i < a.length; i++){
        bst.add(a[i], i);
      }

      bst.travel();
    }

}

编译运行：

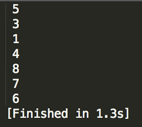
由于比较好理解，所以这里就不一一debug遍历方法去了，总之是首先先打印当前结点，之后再递归左右子树，刚好跟前序遍历的定义一样。

中序遍历：

同样对于上面的二叉数用前序遍历，遍历过程如下：

1、先遍历左节点

　　继续按着左中右的遍历顺序继续对左子树进行遍历，如下：
　　a、先遍历左节点，由于只有一个结点直接打印【1】

　　b、再遍历根节点【3】

　　c、最后再遍历右节点【4】

2、再遍历根节点【5】

3、最后再遍历右节点：

　　继续按着左中右的遍历顺序继续对右子树进行遍历，如下：
　　a、先遍历左节点
　　　　

　　　　　　aa、先遍历左节点【6】

　　　　　　ab、再遍历根节点【7】

　　　　　　ac、最后再遍历右节点，由于木有右节点直接结束递归。　　　　　　　　　　　　

　　b、再遍历根节点【8】

　　c、最后再遍历右节点，由于木有右节点直接结束递归。

至此整个中序遍历结束，结果如：【1】、【3】、【4】、【5】、【6】、【7】、【8】

【提示】：有木有发现居然结果成了一组有序的数列，也就是说这又是一种排序的算法：将一组数用组成二叉搜索树之后然后再用中序遍历打印出来，当然这种排序算法不是特别好，只是从这个结果点可以联想到排序算法。

下面看下代码具体实现，比较简单，只需要简单修改travel的打印顺序既可，如下：

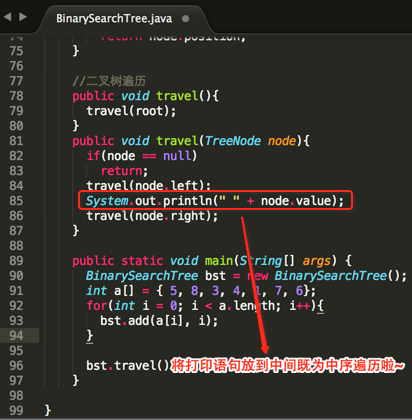
编译运行：

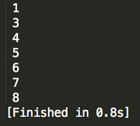,跟预期一致。

后序遍历：

同理，对于上面的二叉数用后序遍历，遍历过程如下：

1、先遍历左节点

　　

　　继续按着左右中的遍历顺序继续对左子树进行遍历，如下：
　　a、先遍历左节点，由于只有一个结点直接打印【1】

　　b、再遍历右节点【4】

　　c、最后再遍历根节点【3】

2、再遍历右节点

　　继续按着左右中的遍历顺序继续对右子树进行遍历，如下：
　　a、先遍历左节点
　　　　

　　　　　　aa、先遍历左节点【6】

　　　　　　ab、最后再遍历右节点，由于木有右节点直接忽略。
　　　　　　ac、再遍历根节点【7】

　　b、最后再遍历右节点，由于木有右节点直接结束递归。

　　c、再遍历根节点【8】　　　　　　　　　　　 

3、最后遍历根节点【5】

至此整个后序遍历结束，结果如：【1】、【4】、【3】、【6】、【7】、【8】、【5】

下面看下代码具体实现，同理只需要简单修改travel的打印顺序既可，如下：

编译运行：

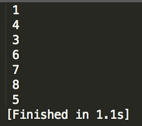，跟预期一致~

那以上的遍历方法的时间复杂度是多少呢？一个结点只访问一次，自然复杂度是O（n），其中n为结点个数。