蚁群算法求解TSP问题
一、蚁群算法简介
蚁群算法是对自然界蚂蚁的寻径方式进行模似而得出的一种仿生算法:蚂蚁在运动过程中,能够在它所经过的路径上留下信息素(pheromone)的物质进行信息传递,而且蚂蚁在运动过程中能够感知这种物质,并以此指导自己的运动方向。由大量蚂蚁组成的蚁群集体行为便表现出一种信息正反馈现象:某一路径上走过的蚂蚁越多,则后来者选择该路径的概率就越大。蚁群算法具有分布计算、信息正反馈和启发式搜索的特征,本质上是进化算法中的一种启发式全局优化算法。
二、TSP问题(旅行商问题)
T S P 问 题 可 以 用 一 个 带 权 完 全 图G=(N,A)来表示,其中N是带有n=|N|点(城市)的集合,A是完全连接这些点的边的集合。每一条边(i,j)属于A都带有一个权值,它代表城市i与城市j之间的距离。TSP问题就是要找到图中的最短哈密尔顿回路。
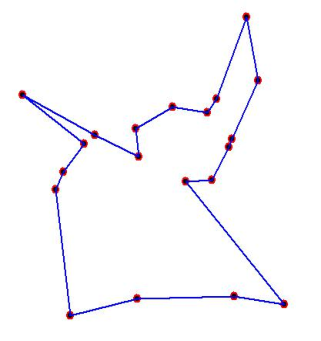
1、构建图:构建图与问题描述图是一致的,成份的集合C对应着点的集合(即:C=N),连接对应着边的集合(即L=A),且每一条边都带有一个权值,代表点i和j之间的距离。
2、约束条件:所有城市都要被访问且每个城市最多只能被访问一次。
3、信息素和启发式信息:TSP 问题中的信息素表示在访问城市i后直接访问城市j的期望度。启发式信息值一般与城市i和城市j的距离成反比。
4、解的构建:每只蚂蚁最初都从随机选择出来的城市出发,每经过一次迭代蚂蚁就向解中添加一个还没有访问过的城市。当所有城市都被蚂蚁访问过之后,解的构建就终止。
三、实现流程及伪代码
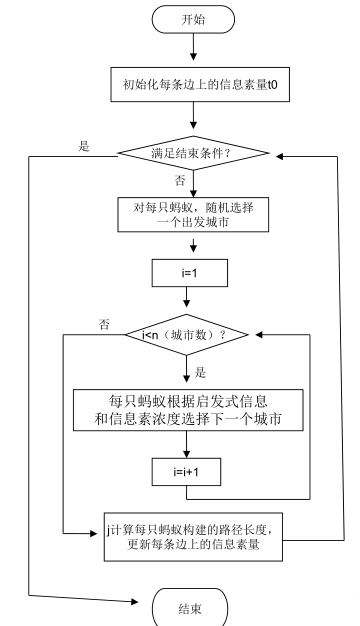

四、代码实现
随机生成50个城市进行测试,初始蚂蚁数量为50,信息素重要程度因子alpha = 1,启发函数重要程度因子beta = 5,信息素挥发因子rho = 0.1,最大迭代次数为150
%% 旅行商问题(TSP)优化
%% 清空环境变量
clear all
clc %% 导入数据
%load citys_data.mat
city = ceil(rand(,) * )
load city.mat
%% 计算城市间相互距离
fprintf('Computing Distance Matrix... \n');
n = size(city,);
D = zeros(n,n);
for i = :n
for j = :n
if i ~= j
D(i,j) = sqrt(sum((city(i,:) - city(j,:)).^));
else
D(i,j) = 1e-;
end
end
end %% 初始化参数
fprintf('Initializing Parameters... \n');
m = ; % 蚂蚁数量
alpha = ; % 信息素重要程度因子
beta = ; % 启发函数重要程度因子
rho = 0.1; % 信息素挥发因子
Q = ; % 常系数
Eta = ./D; % 启发函数
Tau = ones(n,n); % 信息素矩阵
Table = zeros(m,n); % 路径记录表
iter = ; % 迭代次数初值
iter_max = ; % 最大迭代次数
Route_best = zeros(iter_max,n); % 各代最佳路径
Length_best = zeros(iter_max,); % 各代最佳路径的长度
Length_ave = zeros(iter_max,); % 各代路径的平均长度 %% 迭代寻找最佳路径
figure;
while iter <= iter_max
fprintf('迭代第%d次\n',iter);
% 随机产生各个蚂蚁的起点城市
start = zeros(m,);
for i = :m
temp = randperm(n);
start(i) = temp();
end
Table(:,) = start;
% 构建解空间
city_index = :n;
% 逐个蚂蚁路径选择
for i = :m
% 逐个城市路径选择
for j = :n
tabu = Table(i,:(j - )); % 已访问的城市集合(禁忌表)
allow_index = ~ismember(city_index,tabu);
allow = city_index(allow_index); % 待访问的城市集合
P = allow;
% 计算城市间转移概率
for k = :length(allow)
P(k) = Tau(tabu(end),allow(k))^alpha * Eta(tabu(end),allow(k))^beta;
end
P = P/sum(P);
% 轮盘赌法选择下一个访问城市
Pc = cumsum(P);
target_index = find(Pc >= rand);
target = allow(target_index());
Table(i,j) = target;
end
end
% 计算各个蚂蚁的路径距离
Length = zeros(m,);
for i = :m
Route = Table(i,:);
for j = :(n - )
Length(i) = Length(i) + D(Route(j),Route(j + ));
end
Length(i) = Length(i) + D(Route(n),Route());
end
% 计算最短路径距离及平均距离
if iter ==
[min_Length,min_index] = min(Length);
Length_best(iter) = min_Length;
Length_ave(iter) = mean(Length);
Route_best(iter,:) = Table(min_index,:);
else
[min_Length,min_index] = min(Length);
Length_best(iter) = min(Length_best(iter - ),min_Length);
Length_ave(iter) = mean(Length);
if Length_best(iter) == min_Length
Route_best(iter,:) = Table(min_index,:);
else
Route_best(iter,:) = Route_best((iter-),:);
end
end
% 更新信息素
Delta_Tau = zeros(n,n);
% 逐个蚂蚁计算
for i = :m
% 逐个城市计算
for j = :(n - )
Delta_Tau(Table(i,j),Table(i,j+)) = Delta_Tau(Table(i,j),Table(i,j+)) + Q/Length(i);
end
Delta_Tau(Table(i,n),Table(i,)) = Delta_Tau(Table(i,n),Table(i,)) + Q/Length(i);
end
Tau = (-rho) * Tau + Delta_Tau;
% 迭代次数加1,清空路径记录表 % figure;
%最佳路径的迭代变化过程
[Shortest_Length,index] = min(Length_best(:iter));
Shortest_Route = Route_best(index,:);
plot([city(Shortest_Route,);city(Shortest_Route(),)],...
[city(Shortest_Route,);city(Shortest_Route(),)],'o-');
pause(0.3); iter = iter + ;
Table = zeros(m,n); % end
end %% 结果显示
[Shortest_Length,index] = min(Length_best);
Shortest_Route = Route_best(index,:);
disp(['最短距离:' num2str(Shortest_Length)]);
disp(['最短路径:' num2str([Shortest_Route Shortest_Route()])]); %% 绘图
figure()
plot([city(Shortest_Route,);city(Shortest_Route(),)],...
[city(Shortest_Route,);city(Shortest_Route(),)],'o-');
grid on
for i = :size(city,)
text(city(i,),city(i,),[' ' num2str(i)]);
end
text(city(Shortest_Route(),),city(Shortest_Route(),),' 起点');
text(city(Shortest_Route(end),),city(Shortest_Route(end),),' 终点');
xlabel('城市位置横坐标')
ylabel('城市位置纵坐标')
title(['蚁群算法优化路径(最短距离:' num2str(Shortest_Length) ')'])
figure()
plot(:iter_max,Length_best,'b',:iter_max,Length_ave,'r:')
legend('最短距离','平均距离')
xlabel('迭代次数')
ylabel('距离')
title('各代最短距离与平均距离对比')
五、实验结果:
5.1随机生成的50个城市坐标
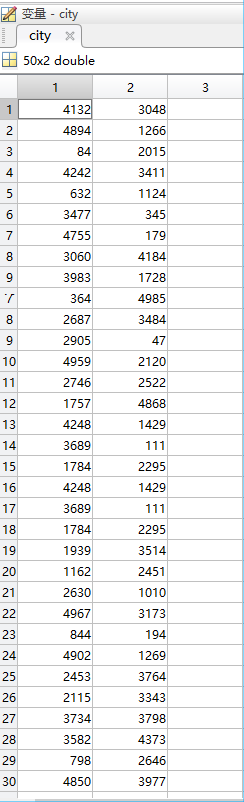

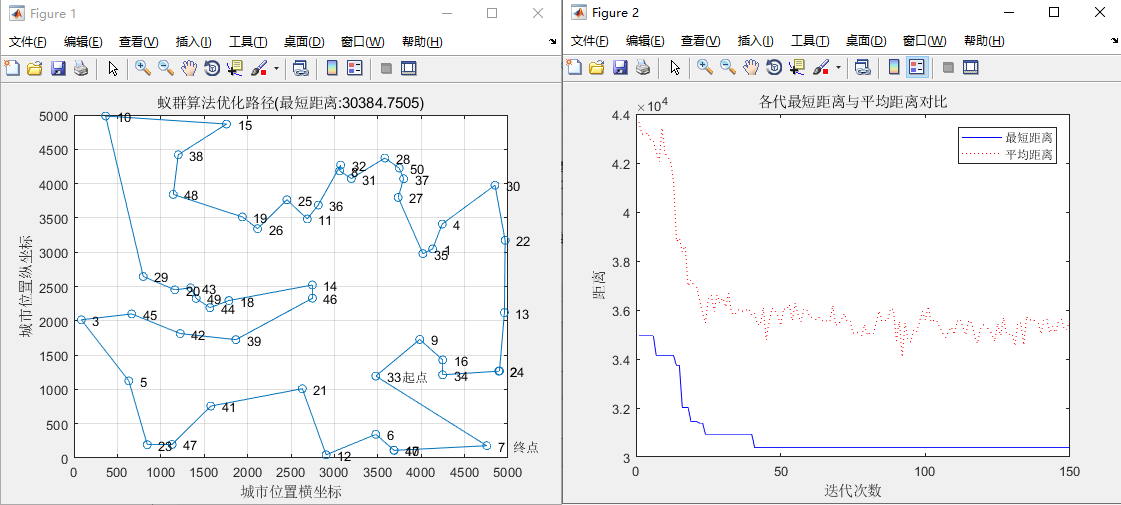
实验数据1:蚂蚁数量为50,信息素重要程度因子alpha = 1,启发函数重要程度因子beta = 5,信息素挥发因子rho = 0.1,最大迭代次数为150


实验数据2:其他数据不变,信息素挥发因子rho = 0.5
实验数据3:其他数据不变,启发函数重要程度因子beta = 3,
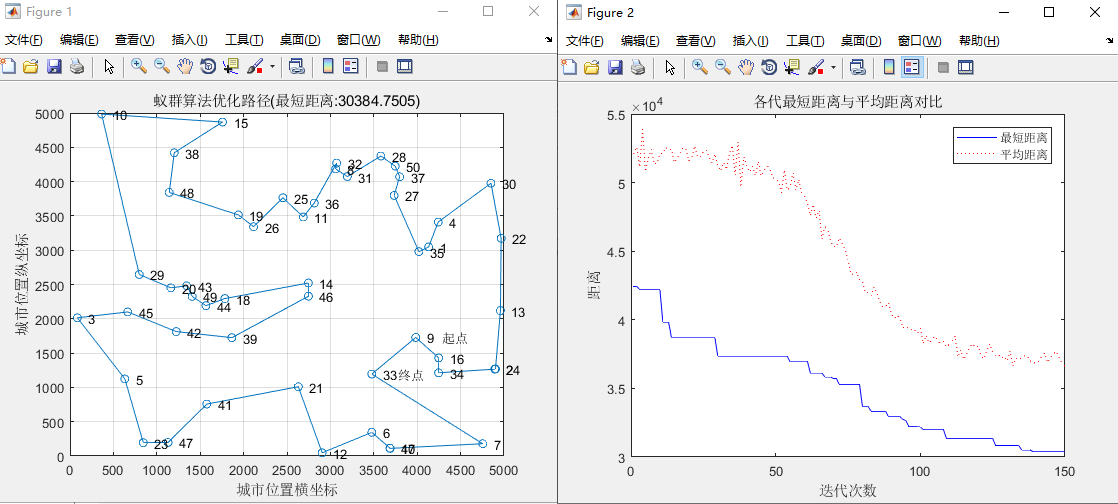
实验数据4:其他数据不变,启发函数重要程度因子beta = 7
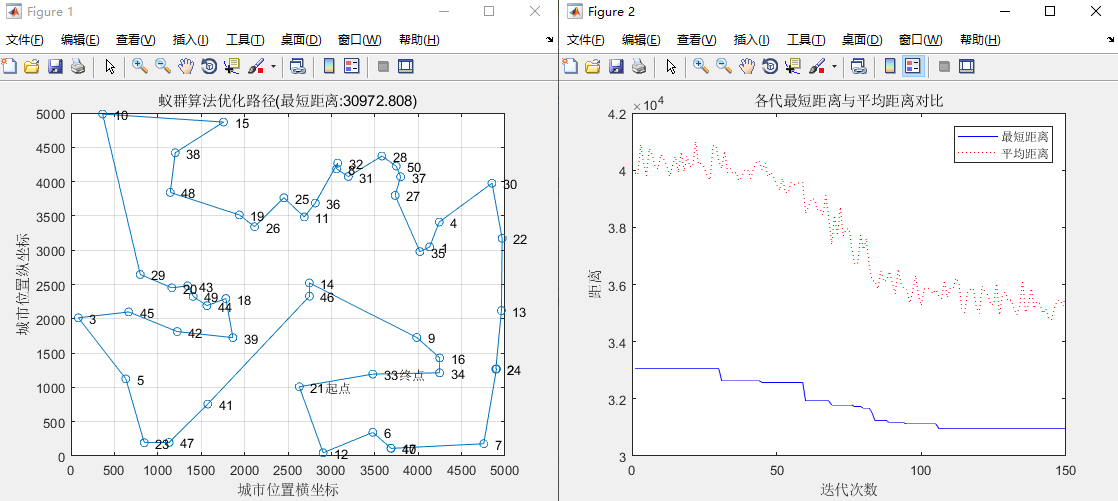
实验数据5:其他数据不变,信息素重要程度因子alpha = 4
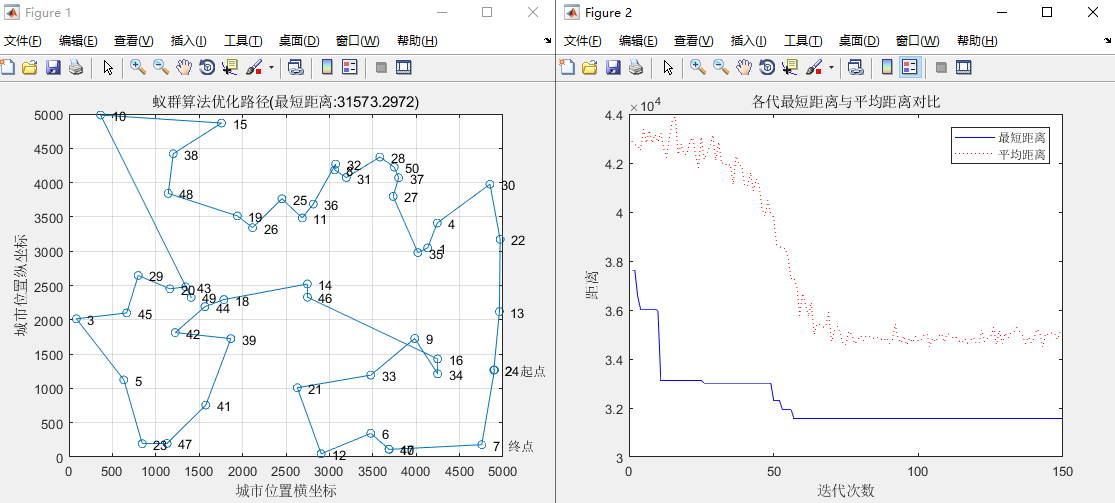
六、结果分析与总结
1、 蚂蚁数量、信息素重要程度因子、启发函数重要程度因子beta、最大迭代次数相同时,rho=0.1与rho=0.5
rho=0.1时,城市序列的起点为39,终点为46。在最短距离的迭代中,迭代次数约为10时,各代的最短距离趋于平缓。当将信息素挥发因子调整为0.5时,可以发现当信息素增大后,最短距离变小,迭代次数约为40时,各代的最短距离就已经趋于平缓。虽然信息素的挥发速度越来越快,但是寻找到的最短路径反而比之前的更短,当rho过小时,未被选中的路径上的信息素量将迅速衰减,容易陷入局部最优,算法的收敛性加大。另外,当rho过大时,被选中的路径上的信息素量增量减小,搜索空间变大,这样算法虽然陷入局部最优的可能性减小,但是算法的收敛性降低。
2、Bete=5与Bete=3、bete=7
当其他因素不变,bete改为3时,发现最短距离变小,且城市序列的起点为9,终点为33。bete=5时,在最短距离的迭代中,在大概10代的时候有一个急剧的减少。但在bete=3时没有极具的下降。在bete=7,迭代过程中开始时就趋于平缓。bete的值反映了启发式信息在指导蚂蚁搜索过程中的重要程度。Bete过小,蚁群陷入随机搜索,就很难找到最优解。Bete过大,蚂蚁在某个局部点上选择局部最短路径的可能性也就越大,但蚁群搜索最优路径的随机性就减弱,容易陷入局部最优。
3、alpha=1与alpha=4
当alpha=1时,在最短距离的迭代中,迭代次数约为10时,各代的最短距离趋于平缓。当alpha=4时,城市序列起点是7,终点是24,最短距离有所增大,但各代的最短距离的迭代趋势和alpha=1时差不多。迭代次数在40-55之间时,平均距离有急剧下降的现象而后逐渐趋于平缓。所以,alpha的值越大,蚂蚁选择以前走过的路径的可能性就越大,搜索的随机性就减弱,算法也会早收敛。
蚁群算法求解TSP问题的更多相关文章
- 利用HTML5 Canvas和Javascript实现的蚁群算法求解TSP问题演示
HTML5提供了Canvas对象,为画图应用提供了便利. Javascript可执行于浏览器中, 而不须要安装特定的编译器: 基于HTML5和Javascript语言, 可随时编写应用, 为算法測试带 ...
- ACS蚁群算法求解对称TSP旅行商问题的JavaScript实现
本来以为在了解蚁群算法的基础上实现这道奇怪的算法题并不难,结果实际上大相径庭啊.做了近三天时间,才改成现在这能勉强拿的出手的模样.由于公式都是图片,暂且以截图代替那部分内容吧,mark一记. 1 蚁群 ...
- 蚁群算法求解旅行商问题(附c和matlab源代码)
前几天写了个模拟退火算法的程序,然后又陆陆续续看了很多群智能算法,发现很多旅行商问题都采用蚁群算法来求解,于是开始写蚁群算法的模板.网上关于蚁群算法的理论很多就不再这里赘述了,下面直接上代码和进行简单 ...
- [matlab] 8.蚁群算法解决TSP问题
城市坐标数据下载 密码:07d5 求遍历这52座城市后最后回到最初城市的最短距离 %% 第9章 蚁群算法及MATLAB实现——TSP问题 % 程序9-1 %% 数据准备 % 清空环境变量 clear ...
- 蚁群算法解决TSP问题
代码实现 运行结果及参数展示 alpha=1beta=5 rho=0.1 alpha=1beta=1rho=0.1 alpha=0.5beta=1rho=0.1 概念蚁群算法(AG)是一种模拟蚂蚁觅 ...
- 蚁群算法(Java)tsp问题
1.理论概述 1.1.TSP问题 旅行商问题,即TSP问题(旅行推销员问题.货郎担问题),是数学领域中著名问题之一.假设有一个旅行商人要拜访n个城市,他必须选择所要走的路径,路径的限制是每个城市只 ...
- 基于粒子群算法求解求解TSP问题(JAVA)
一.TSP问题 TSP问题(Travelling Salesman Problem)即旅行商问题,又译为旅行推销员问题.货郎担问题,是数学领域中著名问题之一.假设有一个旅行商人要拜访n个城市,他必须选 ...
- 蚁群算法MATLAB解VRP问题
Excel exp12_3_2.xls内容: ANT_VRP函数: function [R_best,L_best,L_ave,Shortest_Route,Shortest_Length]=ANT ...
- 蚁群算法MATLAB解TSP问题
Excel表exp12_3_1.xls中数据为: clc clear all [xdata,textdata]=xlsread('exp12_3_1.xls'); %加载20个城市的数据,数据按照表格 ...
随机推荐
- fastclick插件中存在的bug
1.在vue项目中安装fastclick插件 npm install --save fastclick 2.在main.js中引入并绑定到body import FastClick from 'fas ...
- 数据库入门(mySQL):创建数据库
基于JetBrains DataGrip创建数据库.SQL语句创建数据库 MySQL数据库存储引擎和数据类型 创建数据库表及基本操作 导出数据库.删除数据库.导入数据库 一.基于JetBrains D ...
- z-index和transform,你真的了解吗?
z-index和transform是CSS中的属性,但很少同学将二者联系到一起,感觉他们八杆子打不上.事实真的是这样吗?如果你也不能确认,这篇文章就值得你花点时间阅读.因为阅读完了,你会有所收获的. ...
- 使用jMeter对基于SAP ID service进行Authentication的Restful API进行并发测试
这篇文章本来Jerry只在SAP社区上写了英文版的,可以通过点击文末的"阅读原文"获得.后来有两位做Marketing Cloud开发的德国同事,写邮件询问关于文章的更多细节,声称 ...
- 页面使用element-tree
<!DOCTYPE html> <html lang="en"> <head> <meta charset="UTF-8&quo ...
- DAY1注册店铺
- 常用git指令记录
Generating an SSH key Checking for existing SSH keys Generating a new SSH key and adding it to the s ...
- java实战(一)-------jdk环境在windows安装及配置
1.jdk官方下载 http://www.oracle.com/technetwork/java/javase/downloads/index.html 点击下载windows的版本:jdk-13.0 ...
- win10锁屏壁纸文件夹Assets中无文件问题的解决方法
一.前言 win10在锁屏时会有很多精美的壁纸,在网上查找到win10锁屏壁纸存放目录为 : C:\Users\你的用户名\AppData\Local\Packages\Microsoft.Windo ...
- Tomcat 启动闪退解决
直接使用cmd进入tomcat 目录下进行启动,直接使用Catalina.bat run运行,查看报啥错.进一步进行解决
