【POJ】1222 EXTENDED LIGHTS OUT（高斯消元）

http://poj.org/problem?id=1222

竟然我理解了两天。。。。。

首先先来了解异或方程组（或者说mod2方程组，modk的话貌似可以这样拓展出来）

对于一些我们需要求出的变量a[1~n]，我们现在知道n个方程组（有解的情况下），每个方程均是类似原版消元那样带了个系数的，只不过这个系数只有0和1，那么我们第i个方程用x[i, 1~n]表示a[1~n]的系数，然后x[n+1]为这个方程的右式

那么这些方程组是这样的

(x[1,1]*a[1])^(x[1,2]*a[2])^...^(x[1,n]*a[n])=x[1, n+1]

(x[2,1]*a[1])^(x[2,2]*a[2])^...^(x[2,n]*a[n])=x[2, n+1]

...

(x[n,1]*a[1])^(x[n,2]*a[2])^...^(x[n,n]*a[n])=x[n, n+1]

而我们知道，异或操作有交换律、结合律。那么对于有一个相同的项，我们要消掉这个项，得到一个相同的方程，我们直接方程异或消掉即可。也就是说，例如两个方程

(x[1,1]*a[1])^(x[1,2]*a[2])^...^(x[1,n]*a[n])=x[1, n+1]

(x[2,1]*a[1])^(x[2,2]*a[2])^...^(x[2,n]*a[n])=x[2, n+1]

当x[1, 1]=x[2, 1]=1时，我们要消掉x[2, 1]，那么我们将这两个式子的所有项都异或就行了，原理就是a=c, b=d, a^b=c^d

然后就能得出个倒三角，最后回代就行了（因为前边的系数都是1了，所以不需要对A[i][i]进行操作）

在找每一列的矩阵时，我们注意只需要找到某一个方程的这一列的系数是1就行了，不需要最大（本来就没有最大），就能消掉所有这一列=1的方程。

然后注意回代的时候系数不是1的就不要异或了（因为本来就没用这个元素啊）

然后记住每次清空矩阵啊！！！我一直以为是我的思路错了，调试了好久，原来是数组没清。。。。

#include <cstdio>
#include <cstring>
#include <cmath>
#include <string>
#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;
#define rep(i, n) for(int i=0; i<(n); ++i)
#define for1(i,a,n) for(int i=(a);i<=(n);++i)
#define for2(i,a,n) for(int i=(a);i<(n);++i)
#define for3(i,a,n) for(int i=(a);i>=(n);--i)
#define for4(i,a,n) for(int i=(a);i>(n);--i)
#define CC(i,a) memset(i,a,sizeof(i))
#define read(a) a=getint()
#define print(a) printf("%d", a)
#define dbg(x) cout << (#x) << " = " << (x) << endl
#define printarr2(a, b, c) for1(_, 1, b) { for1(__, 1, c) cout << a[_][__]; cout << endl; }
#define printarr1(a, b) for1(_, 1, b) cout << a[_] << '\t'; cout << endl
inline const int getint() { int r=0, k=1; char c=getchar(); for(; c<'0'||c>'9'; c=getchar()) if(c=='-') k=-1; for(; c>='0'&&c<='9'; c=getchar()) r=r*10+c-'0'; return k*r; }
inline const int max(const int &a, const int &b) { return a>b?a:b; }
inline const int min(const int &a, const int &b) { return a<b?a:b; }

const int N=35;
typedef int mtx[N][N];
mtx a;
void gauss(mtx A, int n) {
	for1(i, 1, n) {
		int now=i;
		while(!A[now][i] && now<=n) ++now;
		for1(j, 1, n+1) swap(A[now][j], A[i][j]);
		for1(j, i+1, n) if(A[j][i])
			for1(k, i, n+1) A[j][k]^=A[i][k];
	}
	for3(i, n, 1)
		for1(j, i+1, n) if(A[i][j]) A[i][n+1]^=A[j][n+1];
}
int main() {
	int cs=getint();
	for1(ttt, 1, cs) {
		CC(a, 0);
		for1(i, 1, 30) {
			read(a[i][31]);
			a[i][i]=1;
			if(i%6!=1) a[i][i-1]=1;
			if(i%6!=0) a[i][i+1]=1;
			if(i>6) a[i][i-6]=1;
			if(i<25) a[i][i+6]=1;
		}
		gauss(a, 30);
		printf("PUZZLE #%d\n", ttt);
		for1(i, 1, 30) {
			printf("%d ", a[i][31]); if(i%6==0) puts("");
		}
	}
	return 0;
}

---

Description

In an extended version of the game Lights Out, is a puzzle with 5 rows of 6 buttons each (the actual puzzle has 5 rows of 5 buttons each). Each button has a light. When a button is pressed, that button and each of its (up to four) neighbors above, below, right and left, has the state of its light reversed. (If on, the light is turned off; if off, the light is turned on.) Buttons in the corners change the state of 3 buttons; buttons on an edge change the state of 4 buttons and other buttons change the state of 5. For example, if the buttons marked X on the left below were to be pressed,the display would change to the image on the right. 

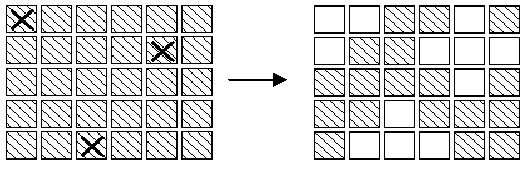The aim of the game is, starting from any initial set of lights on in the display, to press buttons to get the display to a state where all lights are off. When adjacent buttons are pressed, the action of one button can undo the effect of another. For instance, in the display below, pressing buttons marked X in the left display results in the right display.Note that the buttons in row 2 column 3 and row 2 column 5 both change the state of the button in row 2 column 4,so that, in the end, its state is unchanged.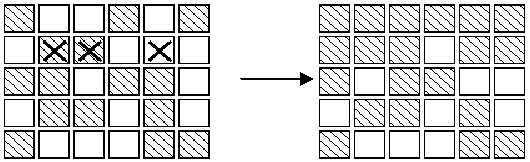 

Note: 
1. It does not matter what order the buttons are pressed. 
2. If a button is pressed a second time, it exactly cancels the effect of the first press, so no button ever need be pressed more than once. 
3. As illustrated in the second diagram, all the lights in the first row may be turned off, by pressing the corresponding buttons in the second row. By repeating this process in each row, all the lights in the first 
four rows may be turned out. Similarly, by pressing buttons in columns 2, 3 ?, all lights in the first 5 columns may be turned off. 
Write a program to solve the puzzle.

Input

The first line of the input is a positive integer n which is the number of puzzles that follow. Each puzzle will be five lines, each of which has six 0 or 1 separated by one or more spaces. A 0 indicates that the light is off, while a 1 indicates that the light is on initially.

Output

For each puzzle, the output consists of a line with the string: "PUZZLE #m", where m is the index of the puzzle in the input file. Following that line, is a puzzle-like display (in the same format as the input) . In this case, 1's indicate buttons that must be pressed to solve the puzzle, while 0 indicate buttons, which are not pressed. There should be exactly one space between each 0 or 1 in the output puzzle-like display.

Sample Input

2
0 1 1 0 1 0
1 0 0 1 1 1
0 0 1 0 0 1
1 0 0 1 0 1
0 1 1 1 0 0
0 0 1 0 1 0
1 0 1 0 1 1
0 0 1 0 1 1
1 0 1 1 0 0
0 1 0 1 0 0

Sample Output

PUZZLE #1
1 0 1 0 0 1
1 1 0 1 0 1
0 0 1 0 1 1
1 0 0 1 0 0
0 1 0 0 0 0
PUZZLE #2
1 0 0 1 1 1
1 1 0 0 0 0
0 0 0 1 0 0
1 1 0 1 0 1
1 0 1 1 0 1

Source

Greater New York 2002