数据库索引（结合B-树和B+树）

数据库索引，是数据库管理系统中一个排序的数据结构以协助快速查询、更新数据库表中数据。索引的实现通常使用B树及其变种B+树。

在数据之外，数据库系统还维护着满足特定查找算法的数据结构，这些数据结构以某种方式引用（指向）数据，这样就可以在这些数据结构上实现高级查找算法。这种数据结构，就是索引。

为表设置索引要付出代价的：一是增加了数据库的存储空间，二是在插入和修改数据时要花费较多的时间(因为索引也要随之变动)。

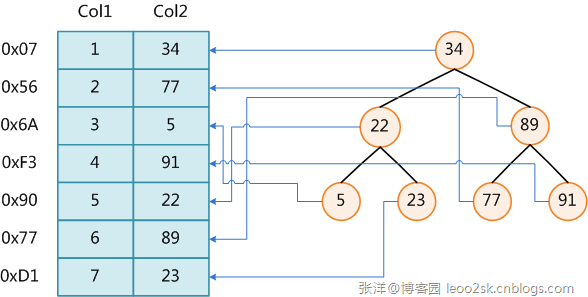
　　上图展示了一种可能的索引方式。左边是数据表，一共有两列七条记录，最左边的是数据记录的物理地址（注意逻辑上相邻的记录在磁盘上也并不是一定物理相邻的）。为了加快Col2的查找，可以维护一个右边所示的二叉查找树，每个节点分别包含索引键值和一个指向对应数据记录物理地址的指针，这样就可以运用二叉查找在O(log₂n)的复杂度内获取到相应数据。

　　

索引的优点：

第一，通过创建唯一性索引，可以保证数据库表中每一行数据的唯一性。

第二，可以大大加快数据的检索速度，这也是创建索引的最主要的原因。

第三，可以加速表和表之间的连接，特别是在实现数据的参考完整性方面特别有意义。

第四，在使用分组和排序子句进行数据检索时，同样可以显著减少查询中分组和排序的时间。

第五，通过使用索引，可以在查询的过程中，使用优化隐藏器，提高系统的性能。

索引的缺点

第一，创建索引和维护索引要耗费时间，这种时间随着数据量的增加而增加。

第二，索引需要占物理空间，除了数据表占数据空间之外，每一个索引还要占一定的物理空间，如果要建立聚簇索引，那么需要的空间就会更大。

第三，当对表中的数据进行增加、删除和修改的时候，索引也要动态的维护，这样就降低了数据的维护速度。

应该在这些列上创建索引：

1、在经常需要搜索的列上，可以加快搜索的速度；

2、在作为主键的列上，强制该列的唯一性和组织表中数据的排列结构；

3、在经常用在连接的列上，这些列主要是一些外键，可以加快连接的速度；

4、在经常需要根据范围进行搜索的列上创建索引，因为索引已经排序，其指定的范围是连续的；

5、在经常需要排序的列上创建索引，因为索引已经排序，这样查询可以利用索引的排序，加快排序查询时间；

6、在经常使用在WHERE子句中的列上面创建索引，加快条件的判断速度。

不应该创建索引的的这些列具有下列特点：

1、对于那些在查询中很少使用或者参考的列不应该创建索引。这是因为，既然这些列很少使用到，因此有索引或者无索引，并不能提高查询速度。相反，由于增加了索引，反而降低了系统的维护速度和增大了空间需求。

2、对于那些只有很少数据值的列也不应该增加索引。这是因为，由于这些列的取值很少，例如人事表的性别列，在查询的结果中，结果集的数据行占了表中数据行的很大比例，即需要在表中搜索的数据行的比例很大。增加索引，并不能明显加快检索速度。

3、对于那些定义为text, image和bit数据类型的列不应该增加索引。这是因为，这些列的数据量要么相当大，要么取值很少。

4、当修改性能远远大于检索性能时，不应该创建索引。这是因为，修改性能和检索性能是互相矛盾的。当增加索引时，会提高检索性能，但是会降低修改性能。当减少索引时，会提高修改性能，降低检索性能。因此，当修改性能远远大于检索性能时，不应该创建索引。

　　根据数据库的功能，可以在数据库设计器中创建三种索引：唯一索引、主键索引和聚集索引。

　　由于存储介质的特性，磁盘本身存取就比主存慢很多，再加上机械运动耗费，磁盘的存取速度往往是主存的几百分分之一，因此为了提高效率，要尽量减少磁盘I/O。为了达到这个目的，磁盘往往不是严格按需读取，而是每次都会预读，即使只需要一个字节，磁盘也会从这个位置开始，顺序向后读取一定长度的数据放入内存。这样做的理论依据是计算机科学中著名的局部性原理：当一个数据被用到时，其附近的数据也通常会马上被使用。程序运行期间所需要的数据通常比较集中。

　　

　　由于磁盘顺序读取的效率很高（不需要寻道时间，只需很少的旋转时间），因此对于具有局部性的程序来说，预读可以提高I/O效率。

　　预读的长度一般为页（page）的整倍数。页是计算机管理存储器的逻辑块，硬件及操作系统往往将主存和磁盘存储区分割为连续的大小相等的块，每个存储块称为一页（在许多操作系统中，页得大小通常为4k），主存和磁盘以页为单位交换数据。当程序要读取的数据不在主存中时，会触发一个缺页异常，此时系统会向磁盘发出读盘信号，磁盘会找到数据的起始位置并向后连续读取一页或几页载入内存中，然后异常返回，程序继续运行。

上文说过一般使用磁盘I/O次数评价索引结构的优劣。先从B-Tree分析，根据B-Tree的定义，可知检索一次最多需要访问h个节点。数据库系统的设计者巧妙利用了磁盘预读原理，将一个节点的大小设为等于一个页，这样每个节点只需要一次I/O就可以完全载入。为了达到这个目的，在实际实现B-Tree还需要使用如下技巧：

每次新建节点时，直接申请一个页的空间，这样就保证一个节点物理上也存储在一个页里，加之计算机存储分配都是按页对齐的，就实现了一个node只需一次I/O。

　　B-Tree中一次检索最多需要h-1次I/O（根节点常驻内存），渐进复杂度为O(h)=O(log_dN)。一般实际应用中，出度d是非常大的数字，通常超过100，因此h非常小（通常不超过3）。

　　而红黑树这种结构，h明显要深的多。由于逻辑上很近的节点（父子）物理上可能很远，无法利用局部性，所以红黑树的I/O渐进复杂度也为O(h)，效率明显比B-Tree差很多。

用B-Tree作为索引结构效率是非常高的

　　

1）B-树

B-Tree是一种多路搜索树（并不是二叉的）：
       1.定义任意非叶子结点最多只有M个儿子；且M>2；
       2.根结点的儿子数为[2, M]；
       3.除根结点以外的非叶子结点的儿子数为[M/2, M]；
       4.每个结点存放至少M/2-1（取上整）和至多M-1个关键字；（至少2个关键字）
       5.非叶子结点的关键字个数=指向儿子的指针个数-1；
       6.非叶子结点的关键字：K[1], K[2], …, K[M-1]；且K[i] < K[i+1]；
       7.非叶子结点的指针：P[1], P[2], …, P[M]；其中P[1]指向关键字小于K[1]的子树，P[M]指向关键字大于K[M-1]的子树，其它P[i]指向关键字属于(K[i-1], K[i])的子树；
       8.所有叶子结点位于同一层。

B-树的特性：
       1.关键字集合分布在整颗树中；
       2.任何一个关键字出现且只出现在一个结点中；
       3.搜索有可能在非叶子结点结束；
       4.其搜索性能等价于在关键字全集内做一次二分查找；
       5.自动层次控制；

　　B-树的搜索，从根结点开始，对结点内的关键字（有序）序列进行二分查找，如果命中则结束，否则进入查询关键字所属范围的儿子结点；重复，直到所对应的儿子指针为空，或已经是叶子结点。

2）B+树

　　B+树非叶节点中存放的关键码并不指示数据对象的地址指针，非叶节点只是索引部分。所有的叶节点在同一层上，包含了全部关键码和相应数据对象的存放地址指针，且叶节点按关键码从小到大顺序链接。如果实际数据对象按加入的顺序存储而不是按关键码次数存储的话，叶节点的索引必须是稠密索引，若实际数据存储按关键码次序存放的话，叶节点索引时稀疏索引。

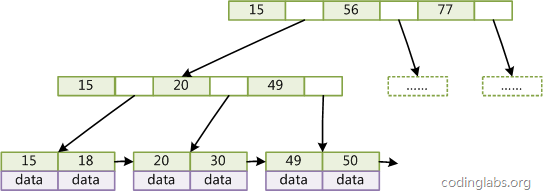
所有的key都会在叶子结点中

（mysql中使用的是B+树作为索引）

B+树的特性：

1.所有关键字都出现在叶子结点的链表中（稠密索引），且链表中的关键字恰好是有序的；

2.不可能在非叶子结点命中；

3.非叶子结点相当于是叶子结点的索引（稀疏索引），叶子结点相当于是存储（关键字）数据的数据层；

4.更适合文件索引系统。

　　在B+Tree的每个叶子节点增加一个指向相邻叶子节点的指针，就形成了带有顺序访问指针的B+Tree。做这个优化的目的是为了提高区间访问的性能。　

　　B+树有2个头指针，一个是树的根节点，一个是最小关键码的叶节点。

所以 B+树有两种搜索方法：

　　一种是按叶节点自己拉起的链表顺序搜索。

　　一种是从根节点开始搜索，和B树类似，不过如果非叶节点的关键码等于给定值，搜索并不停止，而是继续沿右指针，一直查到叶节点上的关键码。所以无论搜索是否成功，都将走完树的所有层。

B+ 树中，数据对象的插入和删除仅在叶节点上进行。

这两种处理索引的数据结构的不同之处：
　　1、B-树中同一键值不会出现多次，并且它有可能出现在叶结点，也有可能出现在非叶结点中。而B+树的键一定会出现在叶结点中，并且有可能在非叶结点中也有可能重复出现，以维持B+树的平衡。
　　2、因为B-树键位置不定，且在整个树结构中只出现一次，虽然可以节省存储空间，但使得在插入、删除操作复杂度明显增加。B+树相比来说是一种较好的折中。
　　3、B-树的查询效率与键在树中的位置有关，最大时间复杂度与B+树相同(在叶结点的时候)，最小时间复杂度为1(在根结点的时候)。而B+树的时候复杂度对某建成的树是固定的。

为什么选用B+、B-树

　　索引本身也很大，不可能全部存储在内存中，因此索引往往以索引文件的形式存储的磁盘上。这样的话，索引查找过程中就要产生磁盘I/O消耗，相对于内存存取，I/O存取的消耗要高几个数量级，所以评价一个数据结构作为索引的优劣最重要的指标就是在查找过程中磁盘I/O操作次数的渐进复杂度。换句话说，索引的结构组织要尽量减少查找过程中磁盘I/O的存取次数。

　　

　　内存读取，内存是由一系列的存储单元组成的，每个存储单元存储固定大小的数据，且有一个唯一地址。当需要读内存时，将地址信号放到地址总线上传给内存，内存解析信号并定位到存储单元，然后把该存储单元上的数据放到数据总线上，回传。

　　写内存时，系统将要写入的数据和单元地址分别放到数据总线和地址总线上，内存读取两个总线的内容，做相应的写操作。

　　内存存取效率，跟次数有关，先读取A数据还是后读取A数据不会影响存取效率。而磁盘存取就不一样了，磁盘I/O涉及机械操作。磁盘是由大小相同且同轴的圆形盘片组成，磁盘可以转动(各个磁盘须同时转动)。磁盘的一侧有磁头支架，磁头支架固定了一组磁头，每个磁头负责存取一个磁盘的内容。磁头不动，磁盘转动，但磁臂可以前后动，用于读取不同磁道上的数据。磁道就是以盘片为中心划分出来的一系列同心环(如图标红那圈)。磁道又划分为一个个小段，叫扇区，是磁盘的最小存储

　　

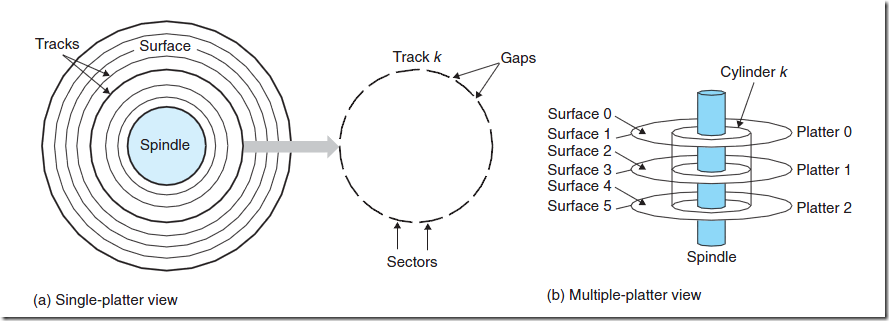
　　磁盘读取时，系统将数据逻辑地址传给磁盘，磁盘的控制电路会解析出物理地址，即哪个磁道哪个扇区。于是磁头需要前后移动到对应的磁道，消耗的时间叫寻道时间，然后磁盘旋转将对应的扇区转到磁头下，消耗的时间叫旋转时间。所以，适当的操作顺序和数据存放可以减少寻道时间和旋转时间。
为了尽量减少I/O操作，磁盘读取每次都会预读，大小通常为页的整数倍。即使只需要读取一个字节，磁盘也会读取一页的数据(通常为4K)放入内存，内存与磁盘以页为单位交换数据。因为局部性原理认为，通常一个数据被用到，其附近的数据也会立马被用到。