【Coursera-ML-Notes】线性回归（下）

模型表示

多变量的线性回归也叫做“多元线性回归”。首先还是先明确几个符号的含义。

• \(x{^{(i)}_j}\)：第i个训练样本的第j个特征，比如面积，楼层，客厅数
• \(x^{(i)}\)：第i个训练样本的输入
• \(m\)：训练样本的数量
• \(n\)：特征的数量

多元线性模型的假设函数的形式如下：
\[
h_θ(x)=θ_0+θ_1x_1+θ_2x_2+θ_3x_3+...+θ_nx_n
\]
对应的\(x_1\)是房子的面积，\(x_2\)是房子的层数，...

用矩阵的形式来表示假设函数可以表示为：

这里让每个样本的第一个特征\(x{^{(i)}_0}\)都等于1。

梯度下降

和一元模型一样，我们只需要将参数收敛的程序做\(n\)次就可以了。

\[
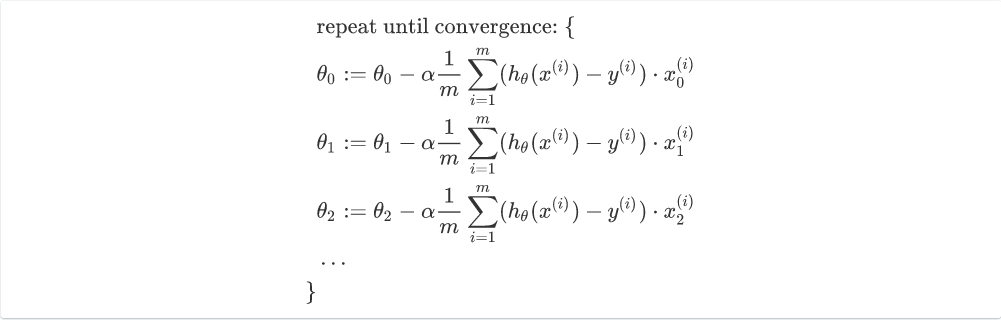
θ=θ-α\frac{1}{m}(X^T(X\cdotθ-y))
\]

加速梯度下降

有两种方法可以帮助我们加速梯度下降，分别是特征缩放和均值归一化。

特征缩放

当特征保持在差不多相同的范围时，梯度下降的速度会快一些。

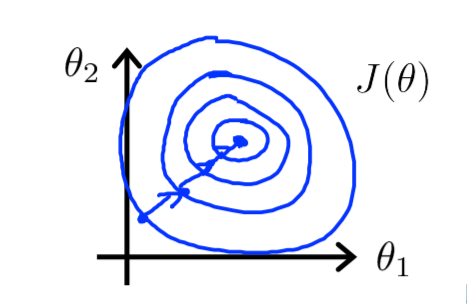
然而实际问题中可能就不这么完美，例如\(x_1\)的范围是0-2000，\(x_2\)的范围是0-5，得到的轮廓图是细长的同心椭圆，收敛所需要的迭代次数因此更多。

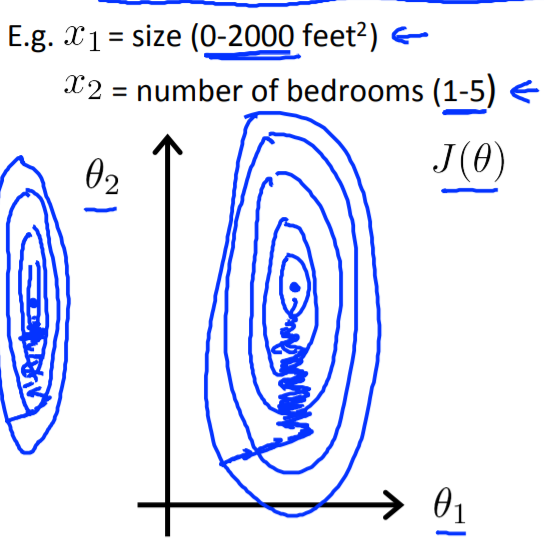
现在通过特征缩放的方法让每一个特征在相同的尺度范围内，让特征除以特征的范围(max-min)。
\[
x_1=\frac{size}{2000},x_2=\frac{number-of-bedrooms}{5}
\]
这样\(x_1,x_2\)的范围都在0-1之间。

均值归一化

均值归一化先减去该特征的平均值\(u_i\)，在除以标准差\(s_i\)或是range(max-min)。
\[
x_i:=\frac{x_i-u_i}{s_i}
\]
例如，\(x_i\)代表房价在100到2000之间，平均值为1000，那么
\[
x_i:=\frac{x_i-1000}{1900}
\]

多项式回归

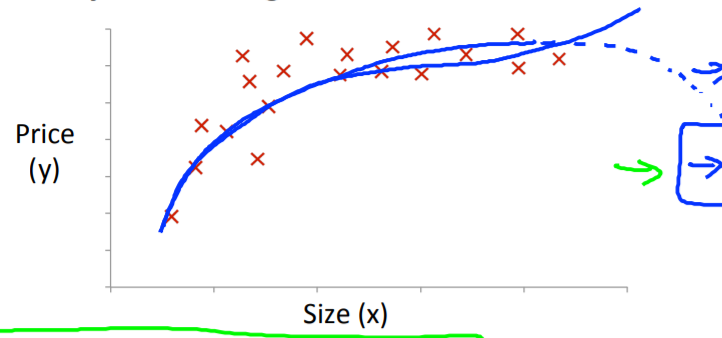
当输入数据的分布是这个样子的，直线的拟合程度是不高的。

可以考虑以一元二次函数来拟合，
\[
h_θ(x)=θ_0+θ_1x_1+θ_2x_2^{2}
\]
但是二次函数随着面积增大后面会下降，这与显示不符，进一步考虑三次函数来拟合
\[
h_θ(x)=θ_0+θ_1x_1+θ_2x_2^{2}+θ_3x_3^3
\]
三次函数会带来巨大的特征范围，这是特征缩放将变得十分重要。因此可以进一步考虑将三次替换为平方根
\[
h_θ(x)=θ_0+θ_1x_1+θ_2x_2^{2}+θ_3\sqrt x_3
\]
这就是多项式回归。

正规方程

在梯度下降中，我们通过调节学习率\(\alpha\)，迭代的算法来求解使得\(J(θ)\)最优的参数解。正规方程的方法不涉及到调参，而是一步直接求出参数\(θ\)。
\[
θ=(X^TX)^{-1}X^Ty
\]

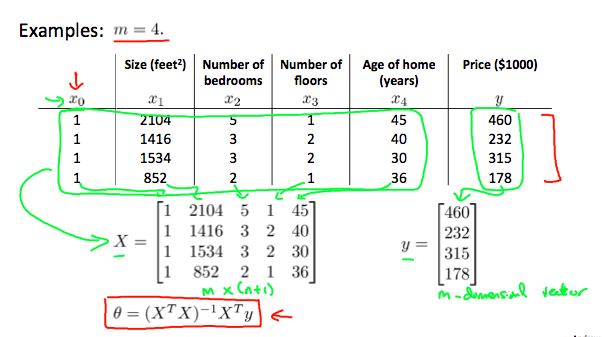
与梯度下降的对比

梯度下降	正规方程
需要调节\(\alpha\)	不需要调节\(\alpha\)
需要多次迭代	一次求出\(θ\)
在特征\(n\)很大时也能很好工作	\(n\)很大时，在求解\((X^TX)\)时时间复杂度很大