[CODE FESTIVAL 2017]Poor Penguin

题意：在一个$n\times m$的网格上，每个格子是薄冰或冰山（网格外什么都没有），有一片薄冰上站着一只企鹅，对于薄冰$(i,j)$，如果不满足（$(i-1,j),(i+1,j)$都有东西或$(i,j-1),(i,j+1)$都有东西），那么它会消失，并且会发生连锁反应，现在你可以把一些冰山削成薄冰，问最少多少次操作可以使得企鹅掉入水中

先考虑什么时候企鹅所在的薄冰会消失（以下的图片全部来自官方题解）

如果一个格子的右下角没有冰山，那么它最终会消失，对其他方向也是这样

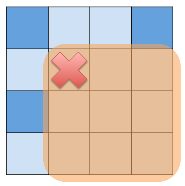
如果能把整个网格用十字分开，使得某两个相对区域中都没有冰山，那么另外两个区域可以被分开考虑，且之后互相独立，这种分割可以递归地进行

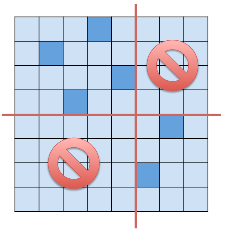
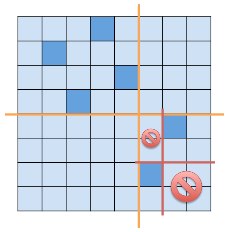
所以对于一个包含企鹅的矩形，我们DP出让它独立于其他格子所需的最小操作次数，再枚举删掉企鹅的四个方向的冰山来更新答案即可

设$f_{i,j,k,l}$表示让$(i,j),(k,l)$这个矩形独立的最小操作次数，枚举它里面的一个点$(x,y)$，以它为中心画十字分开原矩形来转移即可

总时间复杂度$O((nm)^3)$，感觉Atcoder评测机挺快的？

#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
void fmin(int&a,int b){
	if(b<a)a=b;
}
int s[41][41],f[41][41][41][41];
char str[41];
int get(int i,int j,int k,int l){
	if(i>k||j>l)return 0;
	return s[k][l]-s[i-1][l]-s[k][j-1]+s[i-1][j-1];
}
int main(){
	int n,m,i,j,k,l,x,y,sx,sy,ans;
	scanf("%d%d",&n,&m);
	for(i=1;i<=n;i++){
		scanf("%s",str+1);
		for(j=1;j<=m;j++){
			if(str[j]=='P'){
				sx=i;
				sy=j;
			}
			s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+(str[j]=='#');
		}
	}
	memset(f,63,sizeof(f));
	ans=f[0][0][0][0];
	f[1][1][n][m]=0;
	for(i=1;i<=sx;i++){
		for(j=1;j<=sy;j++){
			for(k=n;k>=sx;k--){
				for(l=m;l>=sy;l--){
					fmin(ans,f[i][j][k][l]+min(min(get(i,j,sx,sy),get(i,sy,sx,l)),min(get(sx,j,k,sy),get(sx,sy,k,l))));
					for(x=i;x<=k;x++){
						for(y=j;y<=l;y++){
							if(sx<=x&&sy<=y)fmin(f[i][j][x][y],f[i][j][k][l]+get(i,y+1,x,l)+get(x+1,j,k,y));
							if(sx<=x&&y<=sy)fmin(f[i][y][x][l],f[i][j][k][l]+get(i,j,x,y-1)+get(x+1,y,k,l));
							if(x<=sx&&y<=sy)fmin(f[x][y][k][l],f[i][j][k][l]+get(i,y,x-1,l)+get(x,j,k,y-1));
							if(x<=sx&&sy<=y)fmin(f[x][j][k][y],f[i][j][k][l]+get(i,j,x-1,y)+get(x,y+1,k,l));
						}
					}
				}
			}
		}
	}
	printf("%d",ans);
}