[UOJ336]无限之环

题目的要求就是每个接头都有且仅有一个与其相连的接头，所以不妨给每个接头$1$的流量，对整个网格图黑白染色后（源点$\mathop\rightarrow\limits^\infty$黑点，白点$\mathop\rightarrow\limits^\infty$汇点）跑最大流即可，剩下的问题就是给旋转水管安排合适的费用

把网格中的格子和边都看成点，先对每个格子按照形状向四周连边$(1,0)$，然后用恰当的建图来表示费用和纠正流量

对$1$接头，转一次可以改变流量到相邻的两个接头，转两次可以改变流量到对面的接头

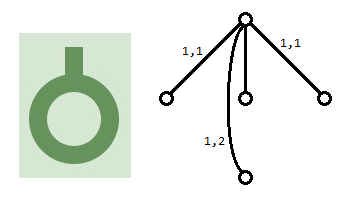
对$2$接头，转一次相当于把一个接头的流量改到对面，连了这两条边后发现恰好满足转两次的需求

对$3$接头，转一次相当于一个接头的流量改到相邻，转两次相当于将$3$个接头中间的接头改到对面，但因为每个接头都只能有$1$的流量经过，所以还要增加一点一边来限流

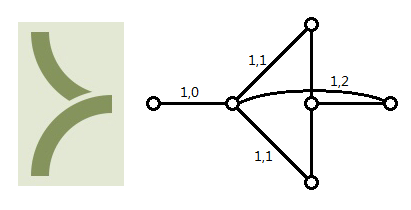
$4$接头就直接连了

总的来说就是两点：1.黑白染色确保能在网格上的边产生流量；2.考虑旋转造成的实际影响，进而构造相应的图

无解就是黑白格接头不相等或跑出来的最大流和黑格接头不相等

#include<stdio.h>
#include<string.h>
#include<queue>
using namespace std;
const int inf=2147483647,go[4][2]={{-1,0},{0,1},{1,0},{0,-1}};
int h[8010],nex[32010],to[32010],cap[32010],cos[32010],M=1,S,T;
void ins(int a,int b,int c,int d){
	M++;
	to[M]=b;
	cap[M]=c;
	cos[M]=d;
	nex[M]=h[a];
	h[a]=M;
}
void add(int a,int b,int c,int d){
	ins(a,b,c,d);
	ins(b,a,0,-d);
}
int dis[8010],sum,cost,N;
struct pr{
	int x,d;
	pr(int u=0):x(u),d(dis[u]){}
}t;
bool operator<(pr a,pr b){return a.d>b.d;}
priority_queue<pr>q;
bool bfs(){
	int x,i;
	memset(dis,63,sizeof(dis));
	dis[T]=0;
	q.push(T);
	while(!q.empty()){
		t=q.top();
		q.pop();
		x=t.x;
		if(t.d!=dis[x])continue;
		for(i=h[x];i;i=nex[i]){
			if(cap[i^1]&&dis[x]-cos[i]<dis[to[i]]){
				dis[to[i]]=dis[x]-cos[i];
				q.push(to[i]);
			}
		}
	}
	sum+=dis[S];
	for(x=1;x<=N;x++){
		for(i=h[x];i;i=nex[i])cos[i]+=dis[to[i]]-dis[x];
	}
	return dis[S]!=dis[0];
}
bool aug[8010];
int dfs(int x,int flow){
	if(flow==0)return 0;
	if(x==T){
		cost+=sum*flow;
		return flow;
	}
	int i,us=0,t;
	aug[x]=1;
	for(i=h[x];i&&flow;i=nex[i]){
		if(cap[i]&&!cos[i]&&!aug[to[i]]){
			t=dfs(to[i],min(flow,cap[i]));
			cap[i]-=t;
			cap[i^1]+=t;
			us+=t;
			flow-=t;
		}
	}
	if(!flow)aug[x]=0;
	return us;
}
int costflow(){
	int s,w;
	s=0;
	do{
		do{
			memset(aug,0,sizeof(aug));
			w=dfs(S,inf);
			s+=w;
		}while(w);
	}while(bfs());
	return s;
}
int cnt[16],rot[16],n,m;
int type(int x){
	if(cnt[x]==2)return x==5||x==10?0:2;
	return cnt[x];
}
int p(int x,int y){
	return(x-1)*m+y;
}
int p(int x,int y,int f){
	f&=3;
	if(f==0)return(x-1)*m+y+n*m;
	if(f==1)return(x-1)*(m+1)+y+1+n*m+(n+1)*m;
	if(f==2)return x*m+y+n*m;
	return(x-1)*(m+1)+y+n*m+(n+1)*m;
}
void gao(int a,int b,int c,int d,int f){
	if(f)
		add(a,b,c,d);
	else
		add(b,a,c,d);
}
int main(){
	int i,j,x,s1,s2;
	for(i=1;i<16;i++)cnt[i]=cnt[i>>1]+(i&1);
	rot[2]=1;
	rot[4]=2;
	rot[6]=1;
	rot[8]=3;
	rot[9]=3;
	rot[11]=3;
	rot[12]=2;
	rot[13]=2;
	rot[14]=1;
	scanf("%d%d",&n,&m);
	S=n*m+(n+1)*m+n*(m+1)+1;
	N=T=S+1;
	s1=s2=0;
	for(i=1;i<=n;i++){
		for(j=1;j<=m;j++){
			scanf("%d",&x);
			if(x==0)continue;
			if((i+j)&1){
				s1+=cnt[x];
				add(S,p(i,j),inf,0);
			}else{
				s2+=cnt[x];
				add(p(i,j),T,inf,0);
			}
			if(x==5){
				gao(p(i,j),p(i,j,0),1,0,(i+j)&1);
				gao(p(i,j),p(i,j,2),1,0,(i+j)&1);
			}
			if(x==10){
				gao(p(i,j),p(i,j,1),1,0,(i+j)&1);
				gao(p(i,j),p(i,j,3),1,0,(i+j)&1);
			}
			switch(type(x)){
				case 1:
					gao(p(i,j),p(i,j,rot[x]),1,0,(i+j)&1);
					gao(p(i,j,rot[x]),p(i,j,rot[x]+1),1,1,(i+j)&1);
					gao(p(i,j,rot[x]),p(i,j,rot[x]+2),1,2,(i+j)&1);
					gao(p(i,j,rot[x]),p(i,j,rot[x]+3),1,1,(i+j)&1);
					break;
				case 2:
					gao(p(i,j),p(i,j,rot[x]),1,0,(i+j)&1);
					gao(p(i,j),p(i,j,rot[x]+1),1,0,(i+j)&1);
					gao(p(i,j,rot[x]),p(i,j,rot[x]+2),1,1,(i+j)&1);
					gao(p(i,j,rot[x]+1),p(i,j,rot[x]+3),1,1,(i+j)&1);
					break;
				case 3:
					gao(p(i,j),p(i,j,rot[x]),1,0,(i+j)&1);
					gao(p(i,j),p(i,j,rot[x]+1),1,0,(i+j)&1);
					gao(p(i,j),p(i,j,rot[x]+2),1,0,(i+j)&1);
					N++;
					gao(p(i,j,rot[x]),N,1,1,(i+j)&1);
					gao(p(i,j,rot[x]+1),N,1,2,(i+j)&1);
					gao(p(i,j,rot[x]+2),N,1,1,(i+j)&1);
					gao(N,p(i,j,rot[x]+3),1,0,(i+j)&1);
					break;
				case 4:
					gao(p(i,j),p(i,j,0),1,0,(i+j)&1);
					gao(p(i,j),p(i,j,1),1,0,(i+j)&1);
					gao(p(i,j),p(i,j,2),1,0,(i+j)&1);
					gao(p(i,j),p(i,j,3),1,0,(i+j)&1);
					break;
			}
		}
	}
	if(s1!=s2||costflow()!=s1)
		puts("-1");
	else
		printf("%d",cost);
}