广度优先搜索--POJ迷宫问题

Description

定义一个二维数组：

int maze[5][5] = {

	0, 1, 0, 0, 0,

	0, 1, 0, 1, 0,

	0, 0, 0, 0, 0,

	0, 1, 1, 1, 0,

	0, 0, 0, 1, 0,

};

它表示一个迷宫，其中的1表示墙壁，0表示可以走的路，只能横着走或竖着走，不能斜着走，要求编程序找出从左上角到右下角的最短路线。

Input

一个5 × 5的二维数组，表示一个迷宫。数据保证有唯一解。

Output

左上角到右下角的最短路径，格式如样例所示。

Sample Input

0 1 0 0 0
0 1 0 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0

Sample Output

(0, 0)
(1, 0)
(2, 0)
(2, 1)
(2, 2)
(2, 3)
(2, 4)
(3, 4)
(4, 4)

分析：这道题很明显是一道寻找最短路径的问题，那就应该选择广度优先搜索，首先来说说广搜吧，广搜的基本思想是这样的：
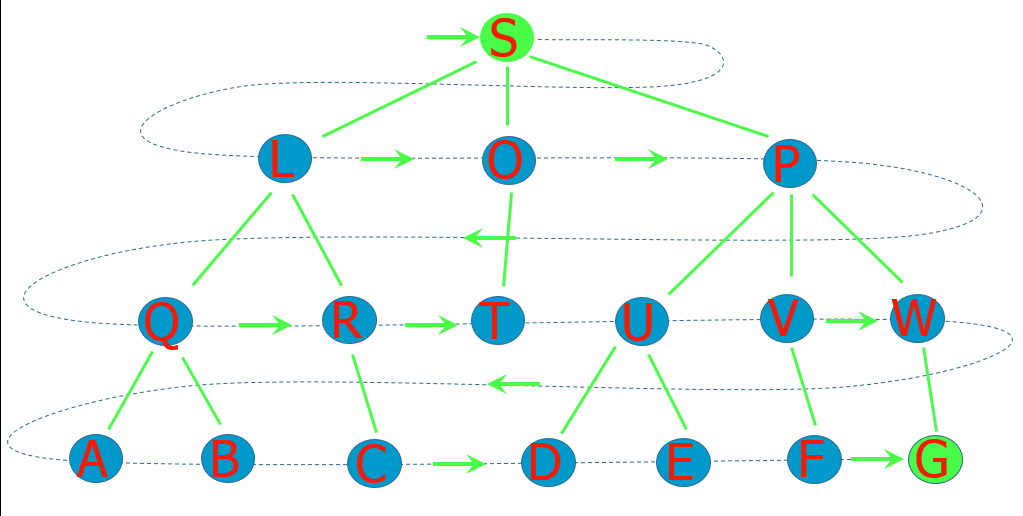
从初始状态S开始，利用规则，生成所有可能的状态。构成树的下一层节点，检查是否出现目标状态G，若未出现，就对该层所有状态节点，分别顺序利用规则。生成再下一层的所有状态节点，对这一层的所有状态节点检查是否出现G，若未出现，继续按上面思想生成再下一层的所有状态节点，这样一层一层往下展开。直到出现目标状态为止。
也就是如下图所示：
                

我们来看一下维基上的代码：

  std::queue<node*> visited, unvisited;
  node nodes[];
  node* current;

  unvisited.push(&nodes[]); //先把root放入unvisited queue

  while(!unvisited.empty()) //只有unvisited不空
  {
     current = (unvisited.front()); //目前應該檢驗的

     if(current -> left != NULL)
        unvisited.push(current -> left); //把左邊放入queue中

     if(current -> right != NULL) //右边压入。因为QUEUE是一个先进先出的结构，所以即使后面再压其他东西，依然会先访问这个。
        unvisited.push(current -> right);

     visited.push(current);

     cout << current -> self << endl;

     unvisited.pop();
  }

首先是有一棵构建好的树，我们从跟节点开始，访问第一层子节点，然后是第二层...这些都应该不难理解。问题是，我们应该怎么初始化这样一棵树，然后怎么记录路径，因为一般给的都只是一个序列，首先你要根据这个序列初始化一棵树然后才能在这棵树的基础上去找。

这里就只考虑迷宫问题吧，首先题目给的是一个二维序列，那么我们就可以直接将这个二维序列看成一棵树，节点就是迷宫路上的每一个格子（非墙），走迷宫的时候，格子间的关系是什么呢？按照题目意思，我们只能横竖走，因此我们可以这样看，格子与它横竖方向上的格子是有连通关系的，只要这个格子跟另一个格子是连通的，那么两个格子节点间就有一条边。如果说本题再修改成斜方向也可以走的话，那么就是格子跟周围8个格子都可以连通，于是一个节点就会有8条边（除了边界的节点）。

下面是记录路径的问题，对于记录路径，我们可以采用回溯法，在每个node里面设一个变量记录它前面的元素，那么在遇到正确结果后就可以以该元素为根往回遍历直到最开始的元素，在每个节点处打印，那这样就把整条路径打印出来了。如：

 struct node{
     int pre;
     int x;
     int y;
 } path[];

 void print(int i) {//当前节点
     if (path[i].pre != -) {//找到前面那个节点
         print(path[i].pre);
         cout << "(" << path[i].x << "," << path[i].y << ")" << endl;
     } else {//最前面的那个节点
         cout << "(" << path[i].x << "," << path[i].y << ")" << endl;
     }
 }

另外一个方法是采用一个stack来专门记录路径，下面我用一个流程来说明：

--》--》...--》--》

--》--》--》...--》--》...--》--》...--》--》

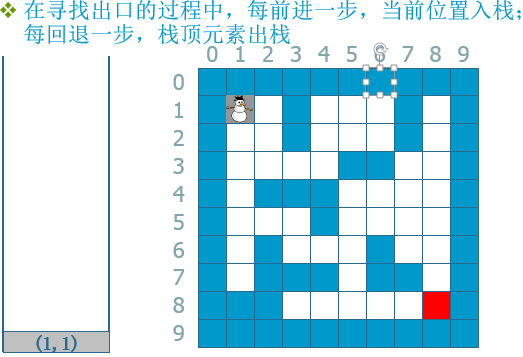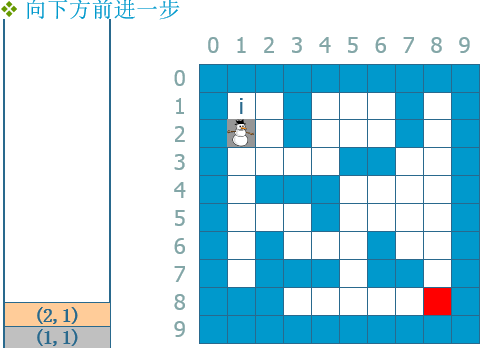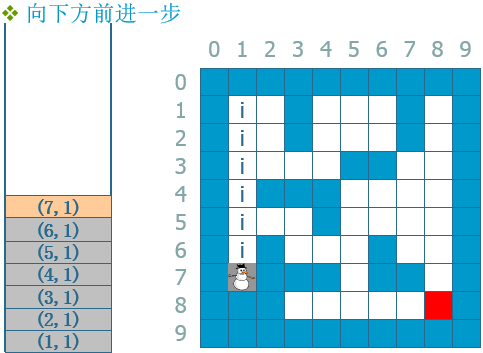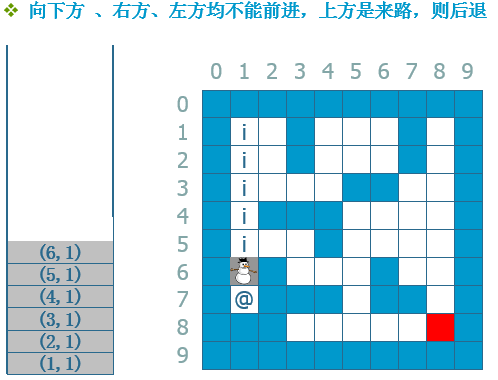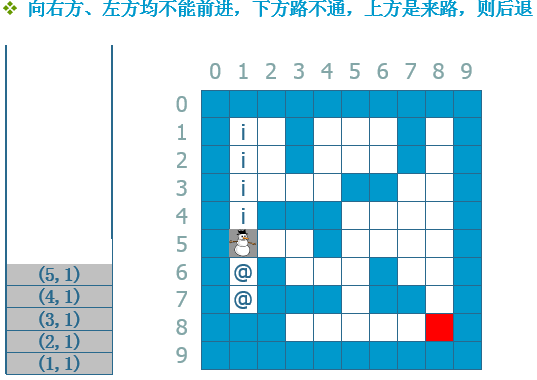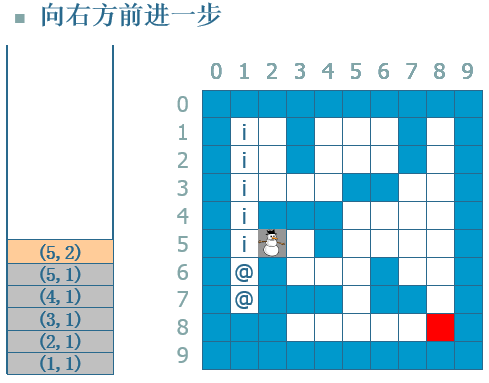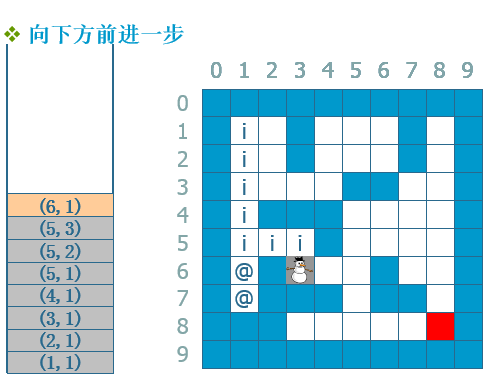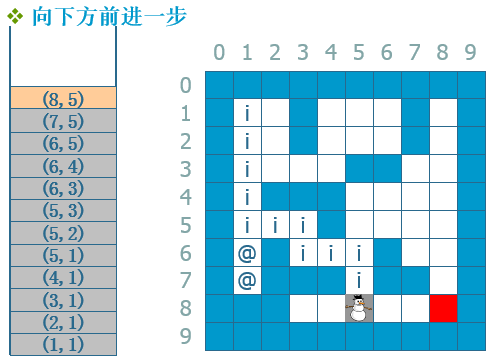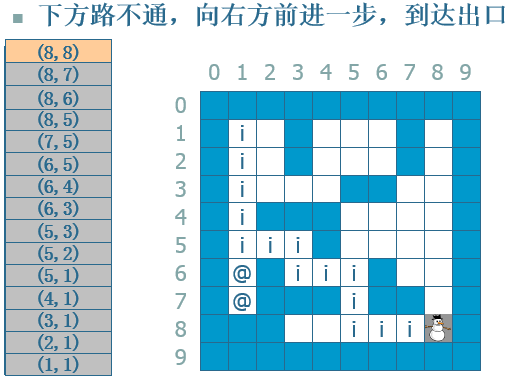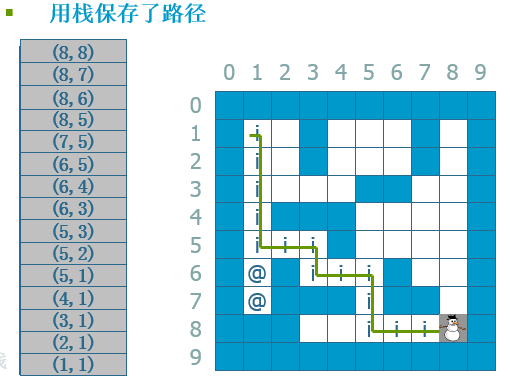
从流程中我们可以看出来了，就不多说了。。。

第三种方法是在node里面设一个list专门记录路径，但是这个方法要记得在每次走到下一个节点的时候将它的父节点的路径记录加上自己的坐标变成自己的路径记录，就像下面这样：

 struct node {
     list<int*> path;
     int x, y;
     node(list<int*> fatherList) {
         path = fatherList;
         int index[] = {x, y};
         path.push_back(index);
     }
 };

那么在找到最后一个的路径的时候就可以直接打印它的path变量。

有人也许会有疑问，为什么广搜找到的路径就是最短了呢？，看看下面这个图你就明白了：

--》

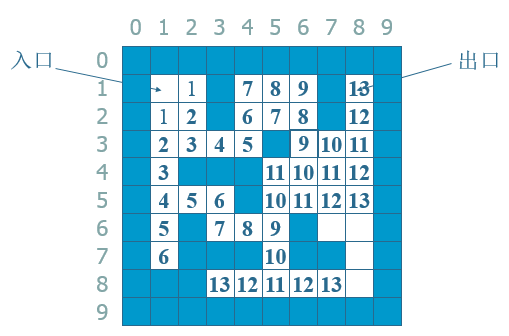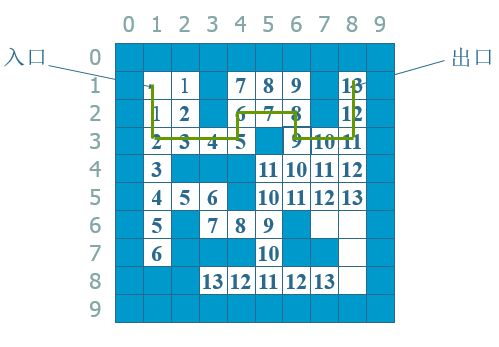
发现数字的规律了吗？数字是分层的，在同一层的数字所代表的路径长度是相同的，一层层的遍历，当某层第一次到达了出口，这层肯定是最短路径所在层啦。

下面是那道题的代码：

 #include <iostream>

 using namespace std;

 int map[][];

 //相邻四个节点
 int borderUponX[] = {, , , -};
 int borderUponY[] = {, -, , };

 int front = , rear = ;

 struct node{
     int pre;
     int x;
     int y;
 } path[];

 void print(int i) {//当前节点
     if (path[i].pre != -) {//找到前面那个节点
         print(path[i].pre);
         cout << "(" << path[i].x << "," << path[i].y << ")" << endl;
     } else {//最前面的那个节点
         cout << "(" << path[i].x << "," << path[i].y << ")" << endl;
     }
 }

 void bfsSearch(int x, int y) {
     //开始节点（出发），前面没有节点了
     path[front].x = x;
     path[front].y = y;
     path[front].pre = -;

     //当front == rear的时候说明已经走完了所以“相邻”节点
     //且都不通
     while (front < rear) {
         for (int i = ; i != ; i++) {
             //相邻节点坐标
             int pathX = path[front].x + borderUponX[i];
             int pathY = path[front].y + borderUponY[i];

             //不符合的节点（遇到边界或已经走过了）
             if (pathY <  || pathX <  || pathX >  || pathY >  || map[pathX][pathY])
                 continue;
             else {//将front的相邻的可以过去的并且是还没有走过的节点加到路径里面
                 map[pathX][pathY] = ;
                 path[rear].x = pathX;
                 path[rear].y = pathY;
                 path[rear].pre = front;
                 rear++;
             }
             if (pathX ==  && pathY == ) {
                 //找到了一条路径，又是第一次找到
                 //那么就是最短路径了
                 print(rear - );
                 break;
             }
         }
         front++;
     }
 }

 int main(int argc, char const *argv[])
 {
     for(int i = ;i < ;i++)
       for(int j = ;j < ;j++)
         cin >> map[i][j];

     bfsSearch(,);
     return ;
 }