清北学堂模拟赛d6t6 棋盘迷宫

3.棋盘迷宫
(boardgame.pas/c/cpp)
(boardgame.in/out)
时间限制:5s/空间限制:256M
【题目描述】
小 A 和小 Z 是非常要好的朋友， 而且他们都对迷宫游戏非常有兴趣。 他们经
常在自习课上用迷宫来打发时间（两位都是学习效率 400%的 dalao， 大家切记不
要模仿） 。
他们的迷宫非常简单， 又被他们叫做是棋盘迷宫， 迷宫本身是一个 N*M 大小
的棋盘， 从左往右列数不断加大， 从上往下行数不断增大， 故左上角的坐标为(1,
1),右下角的坐标为（N,M） 。 当你处在坐标为（X,Y） 的格子里时， 你只能走到
（X+1,Y） 或（X,Y+1） ， 即只能往右走或者往下走（当然你也不能走出棋盘） 。
同时部分格子中有障碍物， 这样的格子是不能经过的， 用‘#’ 代表， 能正常通
行的格子由‘.’ 代表。
每一轮游戏先由其中一人选定起点和终点， 由另外一个人来完成） 。 但是他
们很快发现， 并不是每次都能找到一条从起点到达终点的路径， 两位 dalao 的注
意力立刻从游戏转移到了如何快速判断路径是否存在这个问题上。
当然 dalao 们瞬间得到了算法， 不过他想考考你， 如果你能顺利解决， 也许
就能得到他们两个的签名哦！ （据说是最高级别的因果律护身符， 能让人逢考必
过）
【输入格式】 (boardgame.in)
一共 N  Q  2 行。
第一行两个正整数为 N, M ， 表示棋盘迷宫的行列。
接下来 N 行， 每行一个长度为 M 的字符串， 由‘#’ ‘.’ 两种字符组成
接下来 1 行， 一个正整数 Q ,表示询问的个数
接下来 Q 行， 每行四个正整数 x1,y1,x2,y2 询问点（x1,y1） 到（x2,y2） 是
否有一条合法的路径
数据保证（x1,y1） （x2,y2） 所在的位置都是‘.’ ， 同时 x1<=x2,y1<=y2
【输出格式】 (boardgame.out)
一共 Q 行， 每行一个字符串Yes 或者 No ， 对应每一个询问的答案。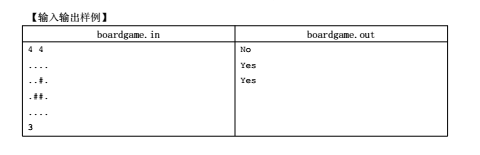

分析：思路比较新奇的一道题。在线做是做不到满分的,只有离线了看看多组询问有什么特征.如果询问点对一个点在图的上半部分，一个点在图的下半部分，那么它们之间的路径肯定要经过中间.考虑一个类似meet in the middle的思想，我们从中间那条线上的点分别向上和向下延伸，看看它能到达哪些点，这样就能处理点对上的点分布在上下两个半图的情况，如果不在同一半图怎么办呢?分治递归就可以了.因为最后点对的两个点肯定要经过中间这条线上的同一个点，所以我们记录f[i][j][k]来表示(i,j)能够到达中间线上的哪些点(k是状态)，最后利用二进制处理一下就好了.标程用了bitset,学了一下，似乎挺好用的.

超多组询问问题我人为要么就是预处理一下，要么就是询问之间肯定有公共类似的部分,从这个公共部分出发，就能通过枚举少数解得到多数解.

#include <cstdio>
#include <bitset>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

int n, m, q, flag[];
char s[][];
bitset <> f[][], g[][];

struct node
{
    int x1, y1, x2, y2, id;
};

void dfs(vector <node> v, int l, int r)
{
    if (l > r)
        return;
    int mid = (l + r) >> ;
    for (int i = mid; i >= l; i--)  //从合法状态扩展到合法状态，必须倒着枚举
        for (int j = m; j >= ; j--)
        {
            f[i][j] = ;
            if (s[i][j] == '.')
            {
                if (i == mid)
                    f[i][j].set(j);
                else
                    f[i][j] |= f[i + ][j];
                if (j != m)
                    f[i][j] |= f[i][j + ];
            }
        }
    for (int i = mid; i <= r; i++)
        for (int j = ; j <= m; j++)
        {
            g[i][j] = ;
            if (s[i][j] == '.')
            {
                if (i == mid)
                    g[i][j].set(j);
                else
                    g[i][j] |= g[i - ][j];
                if (j != )
                    g[i][j] |= g[i][j - ];
            }
        }
    vector <node> vl, vr;
    for (vector <node>::iterator it = v.begin(); it != v.end(); it++)
    {
        node q = *it;
        if (q.x2 < mid)
            vl.push_back(q);
        else
            if (q.x1 > mid)
                vr.push_back(q);
            else
                flag[q.id] = (f[q.x1][q.y1] & g[q.x2][q.y2]).any();
    }
    dfs(vl, l, mid - );
    dfs(vr, mid + , r);
}

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = ; i <= n; i++)
        scanf("%s", s[i] + );
    vector <node> v;
    scanf("%d", &q);
    for (int i = ; i <= q; i++)
    {
        node temp;
        scanf("%d%d%d%d", &temp.x1, &temp.y1, &temp.x2, &temp.y2);
        temp.id = i;
        v.push_back(temp);
    }
    dfs(v, , n);
    for (int i = ; i <= q; i++)
    {
        if (flag[i])
            printf("Yes\n");
        else
            printf("No\n");
    }

    return ;
}