hdu3982 直线切多边形 【WA中...】

题意：有一块蛋糕，上面有一颗cherry。用刀子切n次，求切完之后有cherry的那部分的面积

My solution：

先做一个大矩形，使cake内切于这个大矩形。如图：

然后不断切这个大矩形，每次切割的时候保留与cherry同侧的那部分。最后剩下的就是一个多边形。求该多边形与圆的面积交即可。

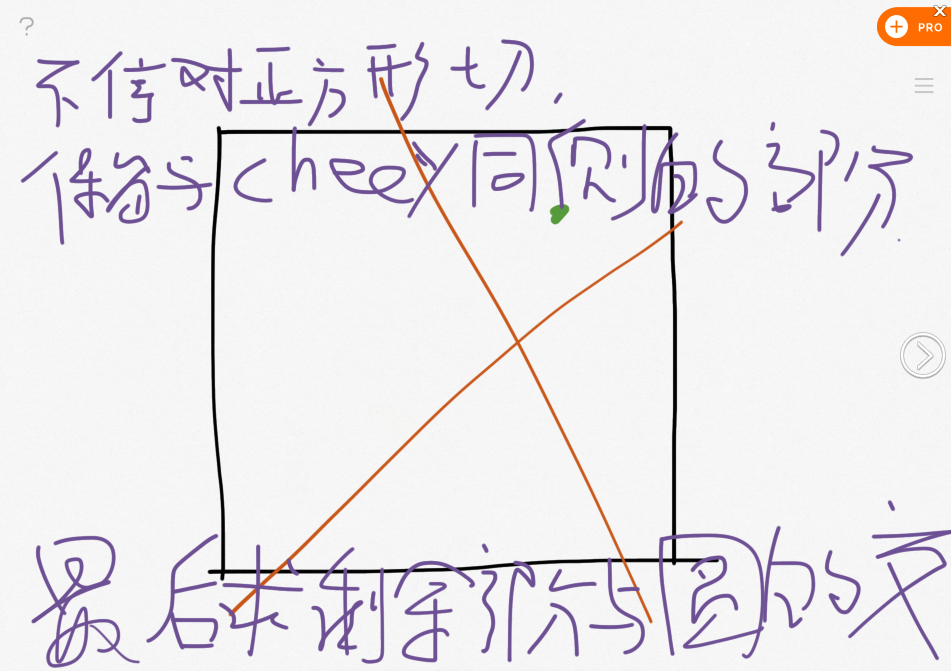
在切割的时候如何保证留下来的是与cherry同侧的部分呢？很简单

方法不难，但是一直WA= =。遇到了个奇怪的问题：

对于这组数据：

3

5 2
-5 0 5 3
-5 0 5 -3
0 0
5 2
-5 0 5 3
-5 0 5 -3
0 4.9
5 2
-5 0 5 3
-5 0 5 -3
0 -4.9

画出来图是这样的：

标程输出结果：

My solution：

可是标程明显不对啊尼玛！加起来都超过1了是什么鬼！

思考ing.........

附WA code：

 #include<vector>
 #include<list>
 #include<map>
 #include<set>
 #include<deque>
 #include<queue>
 #include<stack>
 #include<bitset>
 #include<algorithm>
 #include<functional>
 #include<numeric>
 #include<utility>
 #include<iostream>
 #include<sstream>
 #include<iomanip>
 #include<cstdio>
 #include<cmath>
 #include<cstdlib>
 #include<cctype>
 #include<string>
 #include<cstring>
 #include<cstdio>
 #include<cmath>
 #include<cstdlib>
 #include<ctime>
 #include<climits>
 #include<complex>
 #define mp make_pair
 #define pb push_back
 using namespace std;
 const double eps=1e-;
 const double pi=acos(-1.0);
 const double inf=1e20;
 const int maxp=;
 
 int sgn(double x)
 {
     if (fabs(x)<eps)    return ;
     if (x<)    return -;
         else return ;
 }
 
 int dblcmp(double d)
 {
     if (fabs(d)<eps)return ;
     return d>eps?:-;
 }
 
 inline double sqr(double x){return x*x;}
 
 struct point
 {
     double x,y;
     point(){}
     point(double _x,double _y):
     x(_x),y(_y){};
     void input()
     {
         scanf("%lf%lf",&x,&y);
     }
     void output()
     {
         printf("%.2f %.2f\n",x,y);
     }
     bool operator==(point a)const
     {
         return dblcmp(a.x-x)==&&dblcmp(a.y-y)==;
     }
     bool operator<(point a)const
     {
         return dblcmp(a.x-x)==?dblcmp(y-a.y)<:x<a.x;
     }
 
     point operator +(const point &b)const
     {
         return point(x+b.x,y+b.y);
     }
     point operator -(const point &b)const
     {
         return point(x-b.x,y-b.y);
     }
     point operator *(const double &k)const
     {
         return point(x*k,y*k);
     }
     point operator /(const double &k)const
     {
         return point(x/k,y/k);
     }
     double operator *(const point &b)const
     {
         return x*b.x+y*b.y;
     }
     double operator ^(const point &b)const
     {
         return x*b.y-y*b.x;
     }
 
     double len()
     {
         return hypot(x,y);
     }
     double len2()
     {
         return x*x+y*y;
     }
     double distance(point p)
     {
         return hypot(x-p.x,y-p.y);
     }
     point add(point p)
     {
         return point(x+p.x,y+p.y);
     }
     point sub(point p)
     {
         return point(x-p.x,y-p.y);
     }
     point mul(double b)
     {
         return point(x*b,y*b);
     }
     point div(double b)
     {
         return point(x/b,y/b);
     }
     double dot(point p)
     {
         return x*p.x+y*p.y;
     }
     double det(point p)
     {
         return x*p.y-y*p.x;
     }
     double rad(point a,point b)
     {
         point p=*this;
         return fabs(atan2(fabs(a.sub(p).det(b.sub(p))),a.sub(p).dot(b.sub(p))));
     }
     point trunc(double r)
     {
         double l=len();
         if (!dblcmp(l))return *this;
         r/=l;
         return point(x*r,y*r);
     }
     point rotleft()
     {
         return point(-y,x);
     }
     point rotright()
     {
         return point(y,-x);
     }
     point rotate(point p,double angle)//绕点p逆时针旋转angle角度
     {
         point v=this->sub(p);
         double c=cos(angle),s=sin(angle);
         return point(p.x+v.x*c-v.y*s,p.y+v.x*s+v.y*c);
     }
 };
 
 struct line
 {
     point a,b;
     line(){}
     line(point _a,point _b)
     {
         a=_a;
         b=_b;
     }
     bool operator==(line v)
     {
         return (a==v.a)&&(b==v.b);
     }
     //倾斜角angle
     line(point p,double angle)
     {
         a=p;
         if (dblcmp(angle-pi/)==)
         {
             b=a.add(point(,));
         }
         else
         {
             b=a.add(point(,tan(angle)));
         }
     }
     //ax+by+c=0
     line(double _a,double _b,double _c)
     {
         if (dblcmp(_a)==)
         {
             a=point(,-_c/_b);
             b=point(,-_c/_b);
         }
         else if (dblcmp(_b)==)
         {
             a=point(-_c/_a,);
             b=point(-_c/_a,);
         }
         else
         {
             a=point(,-_c/_b);
             b=point(,(-_c-_a)/_b);
         }
     }
     void input()
     {
         a.input();
         b.input();
     }
     void adjust()
     {
         if (b<a)swap(a,b);
     }
     double length()
     {
         return a.distance(b);
     }
     double angle()//直线倾斜角 0<=angle<180
     {
         double k=atan2(b.y-a.y,b.x-a.x);
         if (dblcmp(k)<)k+=pi;
         if (dblcmp(k-pi)==)k-=pi;
         return k;
     }
     //点和线段关系
     //1 在逆时针
     //2 在顺时针
     //3 平行
     int relation(point p)
     {
         int c=dblcmp(p.sub(a).det(b.sub(a)));
         if (c<)return ;
         if (c>)return ;
         return ;
     }
     bool pointonseg(point p)
     {
         return dblcmp(p.sub(a).det(b.sub(a)))==&&dblcmp(p.sub(a).dot(p.sub(b)))<=;
     }
     bool parallel(line v)
     {
         return dblcmp(b.sub(a).det(v.b.sub(v.a)))==;
     }
     //2 规范相交
     //1 非规范相交
     //0 不相交
     int segcrossseg(line v)
     {
         int d1=dblcmp(b.sub(a).det(v.a.sub(a)));
         int d2=dblcmp(b.sub(a).det(v.b.sub(a)));
         int d3=dblcmp(v.b.sub(v.a).det(a.sub(v.a)));
         int d4=dblcmp(v.b.sub(v.a).det(b.sub(v.a)));
         if ((d1^d2)==-&&(d3^d4)==-)return ;
         return (d1==&&dblcmp(v.a.sub(a).dot(v.a.sub(b)))<=||
                 d2==&&dblcmp(v.b.sub(a).dot(v.b.sub(b)))<=||
                 d3==&&dblcmp(a.sub(v.a).dot(a.sub(v.b)))<=||
                 d4==&&dblcmp(b.sub(v.a).dot(b.sub(v.b)))<=);
     }
     int linecrossseg(line v)//*this seg v line
     {
         int d1=dblcmp(b.sub(a).det(v.a.sub(a)));
         int d2=dblcmp(b.sub(a).det(v.b.sub(a)));
         if ((d1^d2)==-)return ;
         return (d1==||d2==);
     }
     //0 平行
     //1 重合
     //2 相交
     int linecrossline(line v)
     {
         if ((*this).parallel(v))
         {
             return v.relation(a)==;
         }
         return ;
     }
     point crosspoint(line v)
     {
         double a1=v.b.sub(v.a).det(a.sub(v.a));
         double a2=v.b.sub(v.a).det(b.sub(v.a));
         return point((a.x*a2-b.x*a1)/(a2-a1),(a.y*a2-b.y*a1)/(a2-a1));
     }
     double dispointtoline(point p)
     {
         return fabs(p.sub(a).det(b.sub(a)))/length();
     }
     double dispointtoseg(point p)
     {
         if (dblcmp(p.sub(b).dot(a.sub(b)))<||dblcmp(p.sub(a).dot(b.sub(a)))<)
         {
             return min(p.distance(a),p.distance(b));
         }
         return dispointtoline(p);
     }
     point lineprog(point p)
     {
         return a.add(b.sub(a).mul(b.sub(a).dot(p.sub(a))/b.sub(a).len2()));
     }
     point symmetrypoint(point p)
     {
         point q=lineprog(p);
         return point(*q.x-p.x,*q.y-p.y);
     }
 };
 
 struct Vector:public point
 {
     Vector(){}
     Vector(double a,double b)
     {
         x=a;    y=b;
     }
     Vector(point _a,point _b)   //a->b
     {
         double dx=_b.x-_a.x;
         double dy=_b.y-_a.y;
         x=dx;   y=dy;
     }
     Vector(line v)
     {
         double dx=v.b.x-v.a.x;
         double dy=v.b.y-v.a.y;
         x=dx;   y=dy;
     }
     double length()
     {
         return (sqrt(x*x+y*y));
     }
     Vector Normal()
     {
         double L=sqrt(x*x+y*y);
         Vector Vans=Vector(-y/L,x/L);
         return Vans;
     }
 };
 
 struct circle
 {
     point p;
     double r;
     circle(){}
     circle(point _p,double _r):
     p(_p),r(_r){};
     circle(double x,double y,double _r):
     p(point(x,y)),r(_r){};
     circle(point a,point b,point c)//三角形的外接圆
     {
         p=line(a.add(b).div(),a.add(b).div().add(b.sub(a).rotleft())).crosspoint(line(c.add(b).div(),c.add(b).div().add(b.sub(c).rotleft())));
         r=p.distance(a);
     }
     circle(point a,point b,point c,bool t)//三角形的内切圆
     {
         line u,v;
         double m=atan2(b.y-a.y,b.x-a.x),n=atan2(c.y-a.y,c.x-a.x);
         u.a=a;
         u.b=u.a.add(point(cos((n+m)/),sin((n+m)/)));
         v.a=b;
         m=atan2(a.y-b.y,a.x-b.x),n=atan2(c.y-b.y,c.x-b.x);
         v.b=v.a.add(point(cos((n+m)/),sin((n+m)/)));
         p=u.crosspoint(v);
         r=line(a,b).dispointtoseg(p);
     }
     void input()
     {
         p.input();
         scanf("%lf",&r);
     }
     void output()
     {
         printf("%.2lf %.2lf %.2lf\n",p.x,p.y,r);
     }
     bool operator==(circle v)
     {
         return ((p==v.p)&&dblcmp(r-v.r)==);
     }
     bool operator<(circle v)const
     {
         return ((p<v.p)||(p==v.p)&&dblcmp(r-v.r)<);
     }
     double area()
     {
         return pi*sqr(r);
     }
     double circumference()
     {
         return *pi*r;
     }
     //0 圆外
     //1 圆上
     //2 圆内
     int relation(point b)
     {
         double dst=b.distance(p);
         if (dblcmp(dst-r)<)return ;
         if (dblcmp(dst-r)==)return ;
         return ;
     }
     int relationseg(line v)
     {
         double dst=v.dispointtoseg(p);
         if (dblcmp(dst-r)<)return ;
         if (dblcmp(dst-r)==)return ;
         return ;
     }
     int relationline(line v)
     {
         double dst=v.dispointtoline(p);
         if (dblcmp(dst-r)<)return ;
         if (dblcmp(dst-r)==)return ;
         return ;
     }
     //过a b两点 半径r的两个圆
     int getcircle(point a,point b,double r,circle&c1,circle&c2)
     {
         circle x(a,r),y(b,r);
         int t=x.pointcrosscircle(y,c1.p,c2.p);
         if (!t)return ;
         c1.r=c2.r=r;
         return t;
     }
     //与直线u相切 过点q 半径r1的圆
     int getcircle(line u,point q,double r1,circle &c1,circle &c2)
     {
         double dis=u.dispointtoline(q);
         if (dblcmp(dis-r1*)>)return ;
         if (dblcmp(dis)==)
         {
             c1.p=q.add(u.b.sub(u.a).rotleft().trunc(r1));
             c2.p=q.add(u.b.sub(u.a).rotright().trunc(r1));
             c1.r=c2.r=r1;
             return ;
         }
         line u1=line(u.a.add(u.b.sub(u.a).rotleft().trunc(r1)),u.b.add(u.b.sub(u.a).rotleft().trunc(r1)));
         line u2=line(u.a.add(u.b.sub(u.a).rotright().trunc(r1)),u.b.add(u.b.sub(u.a).rotright().trunc(r1)));
         circle cc=circle(q,r1);
         point p1,p2;
         if (!cc.pointcrossline(u1,p1,p2))cc.pointcrossline(u2,p1,p2);
         c1=circle(p1,r1);
         if (p1==p2)
         {
             c2=c1;return ;
         }
         c2=circle(p2,r1);
         return ;
     }
     //同时与直线u,v相切 半径r1的圆
     int getcircle(line u,line v,double r1,circle &c1,circle &c2,circle &c3,circle &c4)
     {
         if (u.parallel(v))return ;
         line u1=line(u.a.add(u.b.sub(u.a).rotleft().trunc(r1)),u.b.add(u.b.sub(u.a).rotleft().trunc(r1)));
         line u2=line(u.a.add(u.b.sub(u.a).rotright().trunc(r1)),u.b.add(u.b.sub(u.a).rotright().trunc(r1)));
         line v1=line(v.a.add(v.b.sub(v.a).rotleft().trunc(r1)),v.b.add(v.b.sub(v.a).rotleft().trunc(r1)));
         line v2=line(v.a.add(v.b.sub(v.a).rotright().trunc(r1)),v.b.add(v.b.sub(v.a).rotright().trunc(r1)));
         c1.r=c2.r=c3.r=c4.r=r1;
         c1.p=u1.crosspoint(v1);
         c2.p=u1.crosspoint(v2);
         c3.p=u2.crosspoint(v1);
         c4.p=u2.crosspoint(v2);
         return ;
     }
     //同时与不相交圆cx,cy相切 半径为r1的圆
     int getcircle(circle cx,circle cy,double r1,circle&c1,circle&c2)
     {
         circle x(cx.p,r1+cx.r),y(cy.p,r1+cy.r);
         int t=x.pointcrosscircle(y,c1.p,c2.p);
         if (!t)return ;
         c1.r=c2.r=r1;
         return t;
     }
     int pointcrossline(line v,point &p1,point &p2)//求与线段交要先判断relationseg
     {
         if (!(*this).relationline(v))return ;
         point a=v.lineprog(p);
         double d=v.dispointtoline(p);
         d=sqrt(r*r-d*d);
         if (dblcmp(d)==)
         {
             p1=a;
             p2=a;
             return ;
         }
         p1=a.sub(v.b.sub(v.a).trunc(d));
         p2=a.add(v.b.sub(v.a).trunc(d));
         return ;
     }
     //5 相离
     //4 外切
     //3 相交
     //2 内切
     //1 内含
     int relationcircle(circle v)
     {
         double d=p.distance(v.p);
         if (dblcmp(d-r-v.r)>)return ;
         if (dblcmp(d-r-v.r)==)return ;
         double l=fabs(r-v.r);
         if (dblcmp(d-r-v.r)<&&dblcmp(d-l)>)return ;
         if (dblcmp(d-l)==)return ;
         if (dblcmp(d-l)<)return ;
     }
     int pointcrosscircle(circle v,point &p1,point &p2)
     {
         int rel=relationcircle(v);
         if (rel==||rel==)return ;
         double d=p.distance(v.p);
         double l=(d+(sqr(r)-sqr(v.r))/d)/;
         double h=sqrt(sqr(r)-sqr(l));
         p1=p.add(v.p.sub(p).trunc(l).add(v.p.sub(p).rotleft().trunc(h)));
         p2=p.add(v.p.sub(p).trunc(l).add(v.p.sub(p).rotright().trunc(h)));
         if (rel==||rel==)
         {
             return ;
         }
         return ;
     }
     //过一点做圆的切线 (先判断点和圆关系)
     int tangentline(point q,line &u,line &v)
     {
         int x=relation(q);
         if (x==)return ;
         if (x==)
         {
             u=line(q,q.add(q.sub(p).rotleft()));
             v=u;
             return ;
         }
         double d=p.distance(q);
         double l=sqr(r)/d;
         double h=sqrt(sqr(r)-sqr(l));
         u=line(q,p.add(q.sub(p).trunc(l).add(q.sub(p).rotleft().trunc(h))));
         v=line(q,p.add(q.sub(p).trunc(l).add(q.sub(p).rotright().trunc(h))));
         return ;
     }
     double areacircle(circle v)
     {
         int rel=relationcircle(v);
         if (rel>=)return 0.0;
         if (rel<=)return min(area(),v.area());
         double d=p.distance(v.p);
         double hf=(r+v.r+d)/2.0;
         double ss=*sqrt(hf*(hf-r)*(hf-v.r)*(hf-d));
         double a1=acos((r*r+d*d-v.r*v.r)/(2.0*r*d));
         a1=a1*r*r;
         double a2=acos((v.r*v.r+d*d-r*r)/(2.0*v.r*d));
         a2=a2*v.r*v.r;
         return a1+a2-ss;
     }
     double areatriangle(point a,point b)
     {
         if (dblcmp(p.sub(a).det(p.sub(b))==))return 0.0;
         point q[];
         int len=;
         q[len++]=a;
         line l(a,b);
         point p1,p2;
         if (pointcrossline(l,q[],q[])==)
         {
             if (dblcmp(a.sub(q[]).dot(b.sub(q[])))<)q[len++]=q[];
             if (dblcmp(a.sub(q[]).dot(b.sub(q[])))<)q[len++]=q[];
         }
         q[len++]=b;
         if (len==&&(dblcmp(q[].sub(q[]).dot(q[].sub(q[])))>))swap(q[],q[]);
         double res=;
         int i;
         for (i=;i<len-;i++)
         {
             if (relation(q[i])==||relation(q[i+])==)
             {
                 double arg=p.rad(q[i],q[i+]);
                 res+=r*r*arg/2.0;
             }
             else
             {
                 res+=fabs(q[i].sub(p).det(q[i+].sub(p))/2.0);
             }
         }
         return res;
     }
 };
 
 struct polygon
 {
     int n;
     point p[maxp];
     line l[maxp];
     void input(int X)
     {
         n=X;
         for (int i=;i<n;i++)
         {
             p[i].input();
         }
     }
     void add(point q)
     {
         p[n++]=q;
     }
     void getline()
     {
         for (int i=;i<n;i++)
         {
             l[i]=line(p[i],p[(i+)%n]);
         }
     }
     struct cmp
     {
         point p;
         cmp(const point &p0){p=p0;}
         bool operator()(const point &aa,const point &bb)
         {
             point a=aa,b=bb;
             int d=dblcmp(a.sub(p).det(b.sub(p)));
             if (d==)
             {
                 return dblcmp(a.distance(p)-b.distance(p))<;
             }
             return d>;
         }
     };
     void norm()
     {
         point mi=p[];
         for (int i=;i<n;i++)mi=min(mi,p[i]);
         sort(p,p+n,cmp(mi));
     }
     void getconvex(polygon &convex)
     {
         int i,j,k;
         sort(p,p+n);
         convex.n=n;
         for (i=;i<min(n,);i++)
         {
             convex.p[i]=p[i];
         }
         if (n<=)return;
         int &top=convex.n;
         top=;
         for (i=;i<n;i++)
         {
             while (top&&convex.p[top].sub(p[i]).det(convex.p[top-].sub(p[i]))<=)
                 top--;
             convex.p[++top]=p[i];
         }
         int temp=top;
         convex.p[++top]=p[n-];
         for (i=n-;i>=;i--)
         {
             while (top!=temp&&convex.p[top].sub(p[i]).det(convex.p[top-].sub(p[i]))<=)
                 top--;
             convex.p[++top]=p[i];
         }
     }
 
     //ADD
     //a new oonvex algorithm
 /*  void Graham(polygon &convex)
     {
         norm();
         int &top=convex.n;
         top=0;
         if (n==1)
         {
             top=1;
             convex.p[0]=p[0];
             return;
         }
         if (n==2)
         {
             top=2;
             convex.p[0]=p[0];
             convex.p[1]=p[1];
             if (convex.p[0]==convex.p[1])   top--;
             return;
         }
         convex.p[0]=p[0];
         convex.p[1]=p[1];
         top=2;
         for (int i=2;i<n;i++)
         {
             while (top>1 && sgn((convex.p[top-1]-convex.p[top-2])^(p[i]-convex.p[top-2]))<=0)
                 top--;
             convex.p[top++]=p[i];
         }
         if (convex.n==2 && (convex.p[0]==convex.p[1]))  convex.n--;
     }
 */
     bool isconvex()
     {
         bool s[];
         memset(s,,sizeof(s));
         int i,j,k;
         for (i=;i<n;i++)
         {
             j=(i+)%n;
             k=(j+)%n;
             s[dblcmp(p[j].sub(p[i]).det(p[k].sub(p[i])))+]=;
             if (s[]&&s[])return ;
         }
         return ;
     }
     //3 点上
     //2 边上
     //1 内部
     //0 外部
     int relationpoint(point q)
     {
         int i,j;
         for (i=;i<n;i++)
         {
             if (p[i]==q)return ;
         }
         getline();
         for (i=;i<n;i++)
         {
             if (l[i].pointonseg(q))return ;
         }
         int cnt=;
         for (i=;i<n;i++)
         {
             j=(i+)%n;
             int k=dblcmp(q.sub(p[j]).det(p[i].sub(p[j])));
             int u=dblcmp(p[i].y-q.y);
             int v=dblcmp(p[j].y-q.y);
             if (k>&&u<&&v>=)cnt++;
             if (k<&&v<&&u>=)cnt--;
         }
         return cnt!=;
     }
     //1 在多边形内长度为正
     //2 相交或与边平行
     //0 无任何交点
     int relationline(line u)
     {
         int i,j,k=;
         getline();
         for (i=;i<n;i++)
         {
             if (l[i].segcrossseg(u)==)return ;
             if (l[i].segcrossseg(u)==)k=;
         }
         if (!k)return ;
         vector<point>vp;
         for (i=;i<n;i++)
         {
             if (l[i].segcrossseg(u))
             {
                 if (l[i].parallel(u))
                 {
                     vp.pb(u.a);
                     vp.pb(u.b);
                     vp.pb(l[i].a);
                     vp.pb(l[i].b);
                     continue;
                 }
                 vp.pb(l[i].crosspoint(u));
             }
         }
         sort(vp.begin(),vp.end());
         int sz=vp.size();
         for (i=;i<sz-;i++)
         {
             point mid=vp[i].add(vp[i+]).div();
             if (relationpoint(mid)==)return ;
         }
         return ;
     }
     //直线u切割凸多边形左侧
     //注意直线方向
     void convexcut(line u,polygon &po)
     {
         int i,j,k;
         int &top=po.n;
         top=;
         for (i=;i<n;i++)
         {
             int d1=dblcmp(p[i].sub(u.a).det(u.b.sub(u.a)));
             int d2=dblcmp(p[(i+)%n].sub(u.a).det(u.b.sub(u.a)));
             if (d1>=)po.p[top++]=p[i];
             if (d1*d2<)po.p[top++]=u.crosspoint(line(p[i],p[(i+)%n]));
         }
     }
     double getcircumference()
     {
         double sum=;
         int i;
         for (i=;i<n;i++)
         {
             sum+=p[i].distance(p[(i+)%n]);
         }
         return sum;
     }
     double getarea()
     {
         double sum=;
         int i;
         for (i=;i<n;i++)
         {
             sum+=p[i].det(p[(i+)%n]);
         }
         return fabs(sum)/;
     }
     bool getdir()//1代表逆时针 0代表顺时针
     {
         double sum=;
         int i;
         for (i=;i<n;i++)
         {
             sum+=p[i].det(p[(i+)%n]);
         }
         if (dblcmp(sum)>)return ;
         return ;
     }
     point getbarycentre()
     {
         point ret(,);
         double area=;
         int i;
         for (i=;i<n-;i++)
         {
             double tmp=p[i].sub(p[]).det(p[i+].sub(p[]));
             if (dblcmp(tmp)==)continue;
             area+=tmp;
             ret.x+=(p[].x+p[i].x+p[i+].x)/*tmp;
             ret.y+=(p[].y+p[i].y+p[i+].y)/*tmp;
         }
         if (dblcmp(area))ret=ret.div(area);
         return ret;
     }
     /*      shen me gui !
     double areaintersection(polygon po)
     {
     }
     double areaunion(polygon po)
     {
         return getarea()+po.getarea()-areaintersection(po);
     }
     */
     double areacircle(circle c)
     {
         int i,j,k,l,m;
         double ans=;
         for (i=;i<n;i++)
         {
             int j=(i+)%n;
             if (dblcmp(p[j].sub(c.p).det(p[i].sub(c.p)))>=)
             {
                 ans+=c.areatriangle(p[i],p[j]);
             }
             else
             {
                 ans-=c.areatriangle(p[i],p[j]);
             }
         }
         return fabs(ans);
     }
     //多边形和圆关系
     //0 一部分在圆外
     //1 与圆某条边相切
     //2 完全在圆内
     int relationcircle(circle c)
     {
         getline();
         int i,x=;
         if (relationpoint(c.p)!=)return ;
         for (i=;i<n;i++)
         {
             if (c.relationseg(l[i])==)return ;
             if (c.relationseg(l[i])==)x=;
         }
         return x;
     }
     void find(int st,point tri[],circle &c)
     {
         if (!st)
         {
             c=circle(point(,),-);
         }
         if (st==)
         {
             c=circle(tri[],);
         }
         if (st==)
         {
             c=circle(tri[].add(tri[]).div(),tri[].distance(tri[])/2.0);
         }
         if (st==)
         {
             c=circle(tri[],tri[],tri[]);
         }
     }
     void solve(int cur,int st,point tri[],circle &c)
     {
         find(st,tri,c);
         if (st==)return;
         int i;
         for (i=;i<cur;i++)
         {
             if (dblcmp(p[i].distance(c.p)-c.r)>)
             {
                 tri[st]=p[i];
                 solve(i,st+,tri,c);
             }
         }
     }
     circle mincircle()//点集最小圆覆盖
     {
         random_shuffle(p,p+n);
         point tri[];
         circle c;
         solve(n,,tri,c);
         return c;
     }
     int circlecover(double r)//单位圆覆盖
     {
         int ans=,i,j;
         vector<pair<double,int> >v;
         for (i=;i<n;i++)
         {
             v.clear();
             for (j=;j<n;j++)if (i!=j)
             {
                 point q=p[i].sub(p[j]);
                 double d=q.len();
                 if (dblcmp(d-*r)<=)
                 {
                     double arg=atan2(q.y,q.x);
                     if (dblcmp(arg)<)arg+=*pi;
                     double t=acos(d/(*r));
                     v.push_back(make_pair(arg-t+*pi,-));
                     v.push_back(make_pair(arg+t+*pi,));
                 }
             }
             sort(v.begin(),v.end());
             int cur=;
             for (j=;j<v.size();j++)
             {
                 if (v[j].second==-)++cur;
                 else --cur;
                 ans=max(ans,cur);
             }
         }
         return ans+;
     }
     int pointinpolygon(point q)//点在凸多边形内部的判定
     {
         if (getdir())reverse(p,p+n);
         if (dblcmp(q.sub(p[]).det(p[n-].sub(p[])))==)
         {
             if (line(p[n-],p[]).pointonseg(q))return n-;
             return -;
         }
         int low=,high=n-,mid;
         while (low<=high)
         {
             mid=(low+high)>>;
             if (dblcmp(q.sub(p[]).det(p[mid].sub(p[])))>=&&dblcmp(q.sub(p[]).det(p[mid+].sub(p[])))<)
             {
                 polygon c;
                 c.p[]=p[mid];
                 c.p[]=p[mid+];
                 c.p[]=p[];
                 c.n=;
                 if (c.relationpoint(q))return mid;
                 return -;
             }
             if (dblcmp(q.sub(p[]).det(p[mid].sub(p[])))>)
             {
                 low=mid+;
             }
             else
             {
                 high=mid-;
             }
         }
         return -;
     }
 
     //ADD
     //最小矩形面积覆盖
     //A必须是凸包（而且是逆时针顺序）
     //Uva   10173
     double cross(point A,point B,point C)
     {}
     double dot(point A,point B,point C)
     {}
     double minRectangleCover(polygon A)
     {}
 
     //ADD
     //直线切凸多边形
     //多边形是逆时针的，在q1q2的左侧
     //HDU3982
     /*
     vector<point> convexcut(const vector<point> &ps,point q1,point q2)
     {
         vector<point> qs;
         int n=ps.size();
         for (int i=0;i<n;i++)
         {
             point p1=ps[i],p2=ps[(i+1)%n];
             int d1=sgn((q2-q1)^(p1-q1)),d2=sgn((q2-q1)^(p2-q1));
             if (d1>=0)
                 qs.push_back(p1);
             if (d1*d2<0)
                 qs.push_back(line(p1,p2).crosspoint(line(q1,q2)));
         }
         return qs;
     }
     */
 };
 
 //ADD
 //直线切凸多边形
 //多边形是逆时针的，在q1q2的左侧
 //HDU3982
 vector<point> convexcut(const vector<point> &ps,point q1,point q2)
 {
     vector<point> qs;
     int n=ps.size();
     for (int i=; i<n; i++)
     {
         point p1=ps[i],p2=ps[(i+)%n];
         int d1=sgn((q2-q1)^(p1-q1)),d2=sgn((q2-q1)^(p2-q1));
         if (d1>=)
             qs.push_back(p1);
         if (d1*d2<)
             qs.push_back(line(p1,p2).crosspoint(line(q1,q2)));
     }
     return qs;
 }
 
 double CutLine[][];
 point Cherry;
 int TotalTimes,n;
 double r;
 
 int main()
 {
     freopen("in.txt","r",stdin);
 
     cin>>TotalTimes;
     for (int Times=;Times<=TotalTimes;Times++)
     {
         //cin>>r>>n;
         scanf("%lf%d",&r,&n);
         circle Cake=circle(point(0.00,0.00),r);
         vector<point> BigPolygon;
         BigPolygon.push_back(point(-r,r));
         BigPolygon.push_back(point(-r,-r));
         BigPolygon.push_back(point(r,-r));
         BigPolygon.push_back(point(r,r));
 
         for (int i=;i<=n;i++)
             scanf("%lf%lf%lf%lf",&CutLine[i][],&CutLine[i][],&CutLine[i][],&CutLine[i][]);
             //cin>>CutLine[i][1]>>CutLine[i][2]>>CutLine[i][3]>>CutLine[i][4];
 
         Cherry.input();
 
         for (int i=;i<=n;i++)
         {
             line cut(point(CutLine[i][],CutLine[i][]),point(CutLine[i][],CutLine[i][]));
             if (cut.relation(Cherry)==)
             {
                 //cut=line(point(CutLine[i][3],CutLine[i][4]),point(CutLine[i][1],CutLine[i][2]));
                 BigPolygon=convexcut(BigPolygon,point(CutLine[i][],CutLine[i][]),point(CutLine[i][],CutLine[i][]));
             }
             else
             {
                 BigPolygon=convexcut(BigPolygon,point(CutLine[i][],CutLine[i][]),point(CutLine[i][],CutLine[i][]));
             }
         }
 
         polygon Bigpolygon;     Bigpolygon.n=;
         for (vector<point>::iterator i=BigPolygon.begin();i!=BigPolygon.end();i++)
         {
             point tmp=*i;
             Bigpolygon.add(tmp);
         }
         //double ans=Bigpolygon.getarea();
         double CakeArea=Cake.area();
         double ans=Bigpolygon.areacircle(Cake);
         ans=ans/CakeArea*;
         printf("Case %d: %.5lf%%\n",Times,ans);
     }
     return ;
 }

Reference：http://blog.csdn.net/zxy_snow/article/details/6739561

话说自从开始刷计算几何之后发现自己代码风格越来越屎了，满满的工程代码既视感。。【逃