2.2 节的练习--Compiler principles, technologys, &tools
2.2 节的练习
2.2.1
考虑下面的上下文无关文法:
S -> S S + | S S * | a
- 试说明如何使用该文法生成串 aa+a*
- 试为这个串构造一颗语法分析树
- ⧗ 该文法生成的语言是什么?试证明
解答
S->SS * ->SS + S * -> aS+ S * -> a a +S* -> a a + a *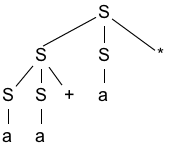
- 把 a 看成是运算数,L = {支持加法和乘法的表达式的后缀表示形式}
2.2.2
下面各个文法生成什么语言?证明你的每一个答案
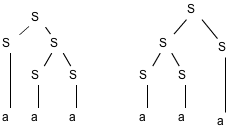
- S -> 0 S 1 | 0 1
- S -> + S S | - S S | a
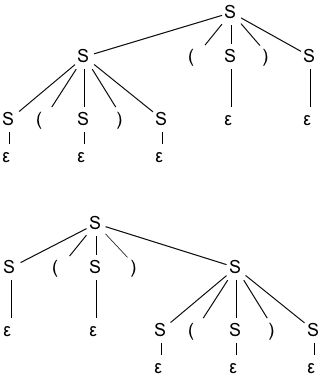
- S -> S ( S ) S | ε
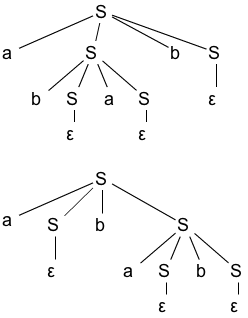
- S -> a S b S | b S a S | ε
- ⧗ S -> a | S + S | S S | S * | ( S )
解答
- L = {0n1n | n>=1}
- L = {支持加法和减法的表达式的前缀表达形式}
- L = {匹配括号的任意排列和嵌套的括号串,包括 ε}
- L = {数量相同的a和b组成的符号串,包括 ε}
- ?
2.2.3
上一题中哪些文法具有二义性
解答
- 没有
- 没有
有
有
有
2.2.4
为下面的各个语言构建无二义性的上下文无关文法。证明你的文法都是正确的。
- 用后缀方法表示的算数表达式
- 由逗号分隔开的左结合的标识符列表(标识符以 id 表示,以下同)
- 由逗号分隔开的右结合的标识符列表
- 有整数、标识符、4个二目运算符 +, -, *, / 构成的算数表达式
- ! 在上一题的运算符中增加单目+ 和单目-构成的算数表达式
解答
- E -> E E op | num
- list -> list , id | id
- list -> id , list | id
expr -> expr + term | expr - term | term
term -> term * factor | term / factor | factor
factor -> id | num | (expr)
注:单目加减运算的优先级最高
expr -> expr + term | expr - term | term
term -> term * unary | term / unary | unary
unary -> + factor | - factor
factor - > id | num | (expr)
2.2.5
证明:用下面文法生成的所有二进制串的值都能被3整除。(提示:对语法分析树的节点树木使用数学归纳法)
num -> 11 | 1001 | num 0 | num num
上面的文法是否能生成所有能被3整除的二进制串?
解答
证明
符合该文法的二进制串一定是由任意数量的 11,1001 和 0 组成的最左位不为0的序列
该序列的十进制和为:
sum
= Σn (21 + 20) * 2 n + Σm (23 + 20) * 2m
= Σn 3 * 2 n + Σm 9 * 2m
显然是能被3整除的
不是。二进制串10101,数值为21,可被3整除,但无法由文法推导出。
注: 还有更一般性的证法么?
2.2.6
为罗马数字构建一个上下文无关文法
注:该文法不考虑罗马数字的上下划线表示,故只能产生小于4k的数字
解答
规则参考 维基百科:罗马数字
根据wiki中讲述的规则,可以发现个位数的表示可以分为4类:
I, II, III | I V | V, V I, V II, V III | I X
即有产生式:
digit -> smallDigit | I V | V smallDigit | I X
smallDigit -> I | II | III | ε
其他数位的表示类似。
还可以发现:罗马数字和阿拉伯数字有比较简单的数位对应关系。
例如:
- XII - X, II - 10 + 2 - 12
- CXCIX - C, XC, IX - 100 + 90 + 9 - 199
- MDCCCLXXX - M, DCCC, LXXX - 1000 + 800 + 80 - 1880
根据这两个规律推导出产生式:
romanNum -> thousand hundred ten digit
thousand -> M | MM | MMM | ε
hundred -> smallHundred | C D | D smallHundred | C M
smallHundred -> C | CC | CCC | ε
ten -> smallTen | X L | L smallTen | X C
smallTen -> X | XX | XXX | ε
digit -> smallDigit | I V | V smallDigit | I X
smallDigit -> I | II | III | ε
2.2 节的练习--Compiler principles, technologys, &tools的更多相关文章
- Compiler Principles 语法分析
语法分析的两种思维方式:1:自顶向下分析 :从语法树的根部推下来一直推到需要确认的终结符号串为止:就是为了找到一个符号串的最左推导 自顶向下分析,因为文法有些是以非终结符开头的另外文法中还可能含有右部 ...
- ACM会议列表与介绍(2014/05/06)
Conferences ACM SEACM Southeast Regional Conference ACM Southeast Regional Conference the oldest, co ...
- Github上的1000多本免费电子书重磅来袭!
Github上的1000多本免费电子书重磅来袭! 以前 StackOverFlow 也给出了一个免费电子书列表,现在在Github上可以看到时刻保持更新的列表了. 瞥一眼下面的书籍分类目录,你就能 ...
- Github 的一个免费编程书籍列表
Index Ada Agda Alef Android APL Arduino ASP.NET MVC Assembly Language Non-X86 AutoHotkey Autotools A ...
- ASP.NET Core 中文文档 第二章 指南(8) 使用 dotnet watch 开发 ASP.NET Core 应用程序
原文:Developing ASP.NET Core applications using dotnet watch 作者:Victor Hurdugaci 翻译:谢炀(Kiler) 校对:刘怡(Al ...
- Hive安装(一)之环境配置
Hive Web Interface(HWI)简介:Hive自带了一个Web-GUI,功能不多,可用于效果展示,如果没有安装Hue的话,是个不错的选择. 由于hive-bin包中没有包含HWI的页面, ...
- Ant自动编译打包&发布 android项目
Eclipse用起来虽然方便,但是编译打包android项目还是比较慢,尤其将应用打包发布到各个渠道时,用Eclipse手动打包各种渠道包就有点不切实际了,这时候我们用到Ant帮我们自动编译打包了. ...
- Core Java Volume I — 3.4. Variables
3.4. VariablesIn Java, every variable has a type. You declare a variable by placing the type first, ...
- 搭建hive1.2.1图形界面
下载:apache-hive-1.2.1-src.tar apache-hive-1.2.1-src.tar 解压,cd apache-hive-1.2.1-src/hwi 命令:jar cfM hi ...
随机推荐
- zipalign内存对齐优化
zipalign:android中SDK下tools文件夹 用来对资源文件的内存进行对齐优化 手工命令: 优化:zipalign -v 4 source.apk destination.apk 4: ...
- 用idea写servlet文件
1:File->Project Structure 加号处添加tomcat api(在lib目录下) 2:写servlet文件 src->new servlet写好类名和包名 3:配置we ...
- UIkit框架之UIcollection
1.继承链:UIScrollView:UIview:UIResponder:NSObject 2.collection view使用的数据源需要遵守UICollectionViewDataSource ...
- angular插件合集
图片视频类 angular-maxonry 图片墙效果插件,可以将图片组织成类似于瀑布流的效果,依赖于jQuery.imageloaded和Masonry angular-deckgrid 另一个照片 ...
- exec函数族,守护进程,线程同步和互斥
2015.3.2 进程和程序有三点不同:1,存在位置不同,程序:硬盘,磁盘.进程:内存2. 程序是静态的,进程是动态的 执行./a.out -->bash->bash程序调用fork()- ...
- OD调试篇8
那么今天需要破解的呢,是这样一款软件. 程序刚刚进去会发现一个nag弹窗 说没有注册,要花20美金才能注册.只有5天的限制期限可以用了 进去之后 点击help里的关于这款软件 也显示了这是一个 ...
- ios 各种技术
1.NSlog 发布后不打印 #ifdef DEBUG// 如果有DEBUG这个宏就编译下面一句代码 #define DDLog(...) NSLog(__VA_ARGS__) #else // 如 ...
- IOS 取消表格单元格 TableViewCell 去掉高亮状态 点击Cell取消选择状态
以下是两种实现效果 1. 自定义cell 继承UITableViewCell 重写 -(void)setSelected:(BOOL)selected animated:(BOOL)animated ...
- 修改mysql用户名密码 和 PHPmysqlAdmin对应密码修改
本地的mysql运行时,可能会用到修改用户名密码: mysql> SET PASSWORD FOR 'root'@'localhost' = PASSWORD('输入新密码');不存在修改用户啊 ...
- C++ 中的对象布局
C++中的涉及到虚表时,类对象的布局分为:虚表与数据成员,子类包含派生类布局,假设下面一个程序: #include <iostream> using namespace std; clas ...
