二叉查找树速通攻略 图文代码精心编写（Java实现）

说在前面

如题目所言

这篇文章为了给下一篇二叉查找数做铺垫和前期知识准备，以便大家有良好的阅读体验，本来想合在一起的，但觉得有些长，所以就拆开了哈哈哈，还是新手向，两篇文章有些长，但如果能认真看下去，实操踩一遍，我认为新手对二叉树的代码实现和基础知识这块，就没什么问题了。当然如果有大佬赐教留言则洗耳恭听哈哈。

符号表

含义

是一个键和一个值联系起来是它的目的，用例可以插入一对键值入表，也可以按键索值，可以按照地图去理解：键就是坐标，地点就是value，概念很简单

分类

有序；无序 ，他们的区别可以暂时粗略认为他们的key前者可以比较，后者则不可

符号表实现方式&二叉查找树的引出

• 链表，数组都可以，前者的实现具有不错的插入性能表现；后者更易于查找，有下标嘛因为，链表的话只能从头遍历，耗时完全取决于输入的目标查找和链表已有长度（计算机硬件性能就不再讨论范围了哈）。
• 但是这两种在面对海量查找和巨大符号表时候，表现糟糕，所以人们就把链表的插入优势和数组的结合，发明了二叉差查找树的数据结构。

好既然说到了树，简单把树的分类大致一说

树tree

• 定义
  
  一种抽象数据结构
• 特点
  
  1.有限节点
  
  2.分层
  
  3.节点之间用链接连接
  
  4.几个术语：度、叶子节点、根结单、父节点、深度高度.....
  
  基本见名知意，个别有不了解的读者可自行百度
• 分类
  
  1.二叉树 ：
  
  图我画的有些丑大家看个意思，懂我说啥就行哈
  
  满二叉树：简单理解就是没有空链接，所以满二叉树一定是完全二叉树
  
  

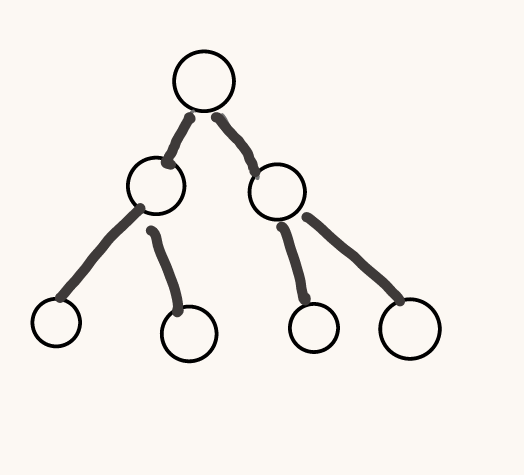
完全二叉树：最后一层从左到右的叶子结点一定要连续，中间不能有空余

第一种：

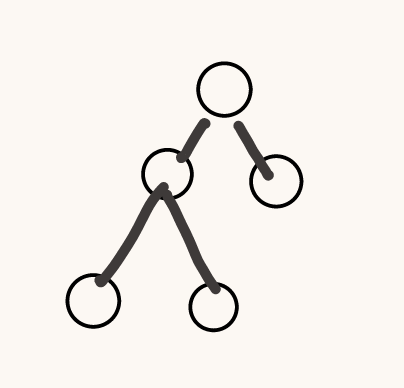
第二种

但是下面这个就不是完全二叉树，因为最下面一层从左到右叶子节点不连续

2.动态查找树：

二叉查找数（二叉树的衍生品）；平衡二叉查找数（2-3树 ，红黑树）；哈夫曼树

这些就是我下一篇重点和大家聊的

3.多路查找数 B树；B+树；B* 树 ，R树（这些就属于‘图’了）

二叉树之二叉查找树

好现在回来，符号表就是二叉树这些东西的预备知识，下面聊二叉查找树

下面的图从左到右表示各种树之间的一种递进关系，或者说右边的是由左边的改造增强而来，并不是包含关系

二叉树

• 基本构成元素：
  
  1.结点，每个节点包含一个键key一个值value，每个节点都只有左右两个链接；分别指向左右节点。
  
  2.链接（允许空链接，单不允许为空键），每个链接都指向一个独立的二叉树

二叉查找树

描述

在二叉树的基础上让键有序允许空键，各子树和他们的父节点的键之间的关系：每个节点的键都大于它左子树任意节点的键而小于右子树任意节点的键

代码实现 ，注释写的很明白，就不过多废话了

点击查看代码

package Tree;

/**
 * @author HuiJixu
 * @version 2.0
 * @since 2021.9
 */
public class BST<Key extends Comparable<Key> ,Value>{
    //BST's root  node
    private Node root;
	//定义节点的结构
    private class Node{
        private  Key key ;
        private Value value ;
        private Node left ,right ;   //指向该节点的子树的左右链接
        private int N ;            //该接待你所包含的节点数目

		//节点构造器
        public Node(Key key , Value value , int  N){
            this.key = key ;
            this.value = value ;
            this.N = N;
        }

        public int size(){return size(root) ;}

        public int size(Node x ){
            if (x == null){
                return  0 ;
            }else{
                return x.N;
            }
        }

        //按键索值
        //这个方法是暴露给用例的方法
        public Value get(Key key){
            return get(root , key);
        }
        //像这种不暴露给用例的方法就要做个封装
        private Value get(Node node, Key key){
            //在以root为根节点的树中查找并返回key对应的值，没有就null
            if (node == null )  return null ;

            //不为空就比较，类似二分法查找
            int temp = key.compareTo(node.key);
            if ( temp < 0 ) return  get(node.left,key);   //将当前节点的左子节点作为新根节点继续往下查找
            else if( temp > 0 ) return get(right.right,key); //将右子树根节点作为新根节点
            else return node.value;
        }
        public void put(Key key , Value value){
            //先查找key，有key则更新，没有就新建节点
            root = put( root , key ,value );
        }

		private Node put(Node node, Key key , Value value ){
            //找不到key说明是新键，那就new 并插入该子树中
            if(node == null) return  new Node(key,value,1) ; //最新的叶子节点只含所有自己一个节点
            //key存在在以当前node为根节点的子树中，就更新它的值
            int temp = key.compareTo(node.key);
            if( temp < 0 ) node.left = put(node.left ,key ,value );
            else if( temp > 0 ) node.right = put(node.right ,key , value ) ;
            else node.value = value ;
            //更新所含有的节点数目
            node.N = size(node.left) + size(node.right) + 1 ;
            return node;
        }

		//delete() 单独说这个方法先把代码放在这里

		public void delete(Key key){
            root = delete(root ,key);
        }
        //在delete操作中，要找出右子树中的最小键对应的value ,并将其作为新的根节点，而作为原先地方的节点就要珊瑚了
        public void deleteMin(){
            root = deleteMin(root);
        }

        public Node deleteMin(Node node){
            //不断检索左子树，直到遇见空节点，则说明该节点就位最小的
            if ( node.left == null) return node.right;
            //不是空的话就继续递归查找左子树
            node.left = deleteMin(node.left);
            //更新节点
            node.N = size(node.right)+ size(node.left) + 1 ;
            return  node;
        }

        private Node delete(Node node , Key key ){
            //空的就直接返回
            if (node == null) return  null ;
            //二分查找非空 .递归查找
            int temp = key.compareTo(node.key);
            if( temp < 0 ) node.left = delete(node.left , key);
            else if( temp > 0 ) node.right = delete(node , key);
            //找到了就删除
            else {
                //下一个是空的返回另一边
                if( node.left == null) return node.right ;
                else if ( node.right == null) return node.right ;
                //两边都不为空
                Node t = node ;   // 保存指向即将被删除的节点的链接
                t = min(node.right);  //将该链接重新指向要被删除的节点的后继节点（下文解释后继节点）
                node.right = deleteMin(t.right); //将要被删除的节点指向删除后仍然所有节点都大于node.key的													//子二叉树，保证树的有序性不变
                node.left = t.left ;  // 左链接保持一致
            }
            //更新删除后节点所含有子节点数
            node.N = size(node.left) + size(node.right) + 1 ;
            return  node ;
        }

        //返回最小值的节点的键
//        其实这样的话如果root节点过高的话，查询效率会首先与树的深度
        public Key min(){
            return min(root).key;
        }
        private Node min(Node node){
            if (node.left == null) return  node ;
            return min(node.left) ;
        }

    }
}

二叉查找树的delete()方法

• 分析
  
  为了方便叙述，我们约定被删除的节点记为node ,其左节点为node.left ; 右节点为node.right ,记指向node的链接为t
  
  要删除一个节点，三件事：1.删除node 2. 将被node的左右子树父节点更新 3.更新该树的相关路径上的节点所包含的子节点个数
  
  把1和2和起来考虑其实就是把node留下的坑填上，有两个方法一种思路：method1：在左子树找出最大的前置节点；method2：在右子树中找出最小后置节点。两者都是为了保持树的有序性。这里代码选择method1，那么就需要一个找出最小节并将其在原位置删除并且返回该最小节点的方法，实现思路就是一直沿着左子树找直到null；代码在上面名为deleteMin(Node node)。
• 实现步骤 ，我图画的是丑了写，但是意思到了哈
  
  初始状态
  
  
  
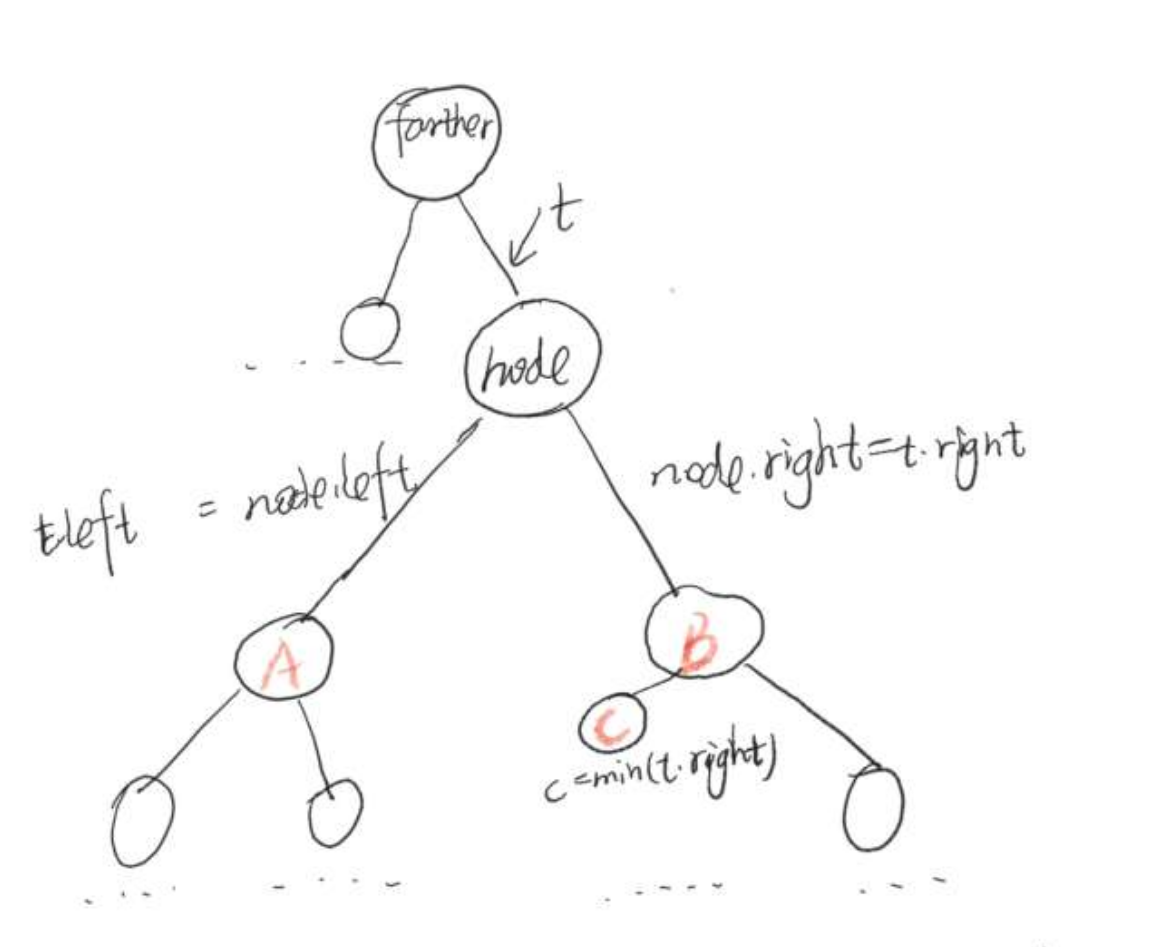
  1、保存指向 node 链接 t
  
  
  
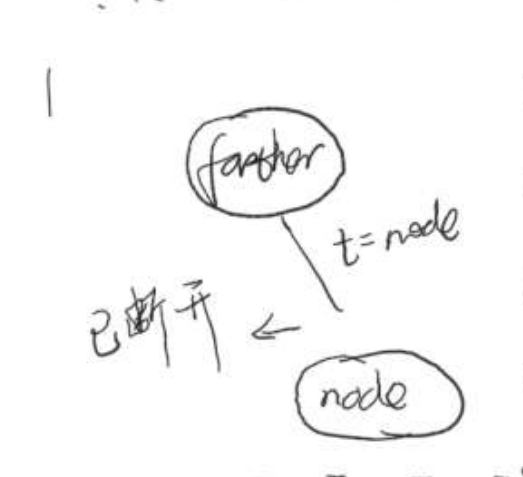
  2、将node 指向它的后继节点
  
  

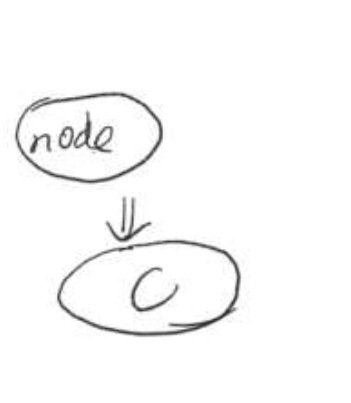
3、将node的右链接指向删除后仍然都大于node.key的子二叉树



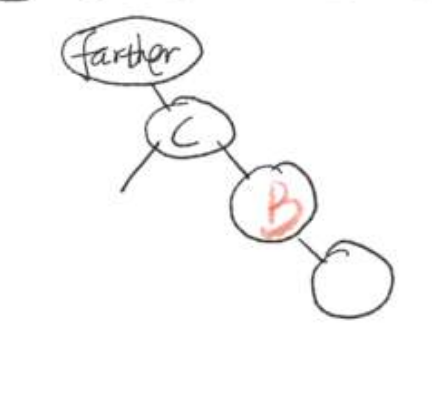
4、将node的左链接设为 t.left

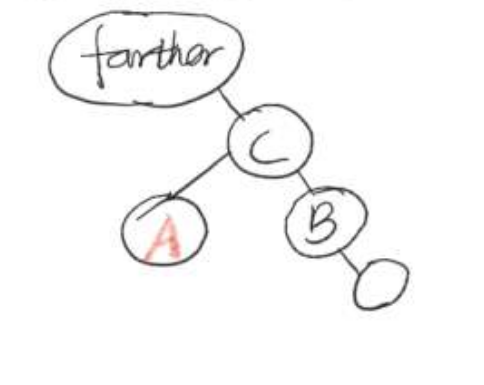
整理不易，觉得还不错不妨点个赞在走嗷！

平衡二叉查找树在下一篇文章