Lepton 无损压缩原理及性能分析

作者：vivo 互联网数据库团队- Li Shihai

本文主要介绍无损压缩图片的概要流程和原理，以及Lepton无损压缩在前期调研中发现的问题和解决方案。

一、从一个游戏开始

1.1 游戏找茬

请拿出你的秒表计时，在15秒时间内找出下面图片的差异。

时间到了，你发现两张图片的差异了吗？

二、智者的成长

在上面的游戏中，你可能你并没有发现两张图片间有任何差异，而实际上它们一张是3.7MB的jpg格式的原图，另外一张是大小为485KB的jpg格式压缩图片，只是大小不同。你可能会有些生气，愤愤不平到这是欺骗，然而聪明的你很快在大脑中产生了一连串的疑问，这些问号让你层层揭开游戏的面纱，不在为愚弄而悔恨，反而从新知中获得快乐。

2.1 苏格拉底助产术

• 上面图片为何变小了呢？
• 丢失了的信息去哪了呢？
• 为什么图片质量下降了，我却看不出来呢？
• 我还能将它变的更小吗？
• 我能将它还原成原来的大小吗？
• 为什么要压缩我的图片？

上面图片为何变小了？图片从3.7MB变成485KB是因为我使用了图片查看工具将原图另存成一张新的图片，在另存的过程中，有一个图片质量选择的参数，我选择了质量最低，保存后便生成了一张更小的图片。可是图片质量下降了，为什么看不出来呢？这就需要了解图片压缩的原理。

2.2  探求表象背后的故事

利用人眼的弱点。

人的视网膜上有两种细胞，视锥细胞和视杆细胞。视锥细胞用来感知颜色，视杆细胞用来感知亮度。而相对于颜色，我们对明暗的感知更明显。

因此可以采取对颜色信息进行压缩来减小图片的大小。

所以我们在图片压缩前会进行颜色空间的变换，JPEG图片通常会变换成YCbCr颜色空间，Y代表亮度，Cb蓝色色彩度，Cr红色色彩度，变换后我们更容易处理色彩部分。然后我们将一张图片切成一块块8*8的像素块，然后使用离散余弦转换算法(DCT)计算出高频区和低频区。

由于人眼对高频区的复杂信息不敏感，因此可以对这一部分进行压缩，这个过程叫量化。最后再将新的文件进行打包。这个流程下来就完成了图片的压缩。

基本流程如下图：

JPEG压缩有损。

在上面的流程中，在预测模块的颜色空间转换后，通过舍弃部分颜色浓度信息，提高压缩率。常见选项为4:2:0，经过这一步后原来需要8个数字表示的信息，现在只需要2个，直接抛弃了75%的Cb Cr信息，然而这一步骤是不可逆的，也就造成了图片压缩的有损。此外在熵编码模块，会进一步使用行程长度编码或Huffman编码进一步对图片信息进行压缩，而这一部分的压缩是无损的，是可逆的。

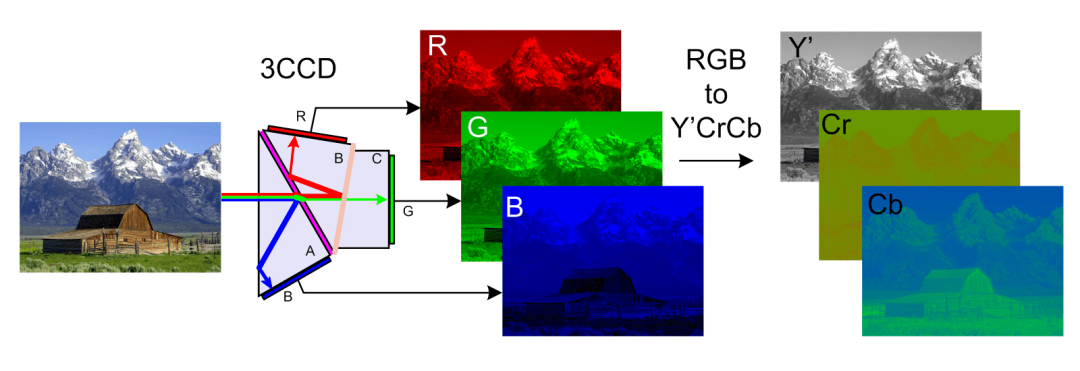
（YCbCr空间转换）

霍夫曼编码原理如下：

假如待编码的字符总共38个符号数据，对其进行统计，得到的符号和对应频度如下表：

首先，对所有符号按照频数大小排序，排序后如下图：

然后，选择两个频数最小的作为叶子节点，频数最小的作为左子节点，另外一个作为右子节点，根节点为两个叶子节点的频数之和。

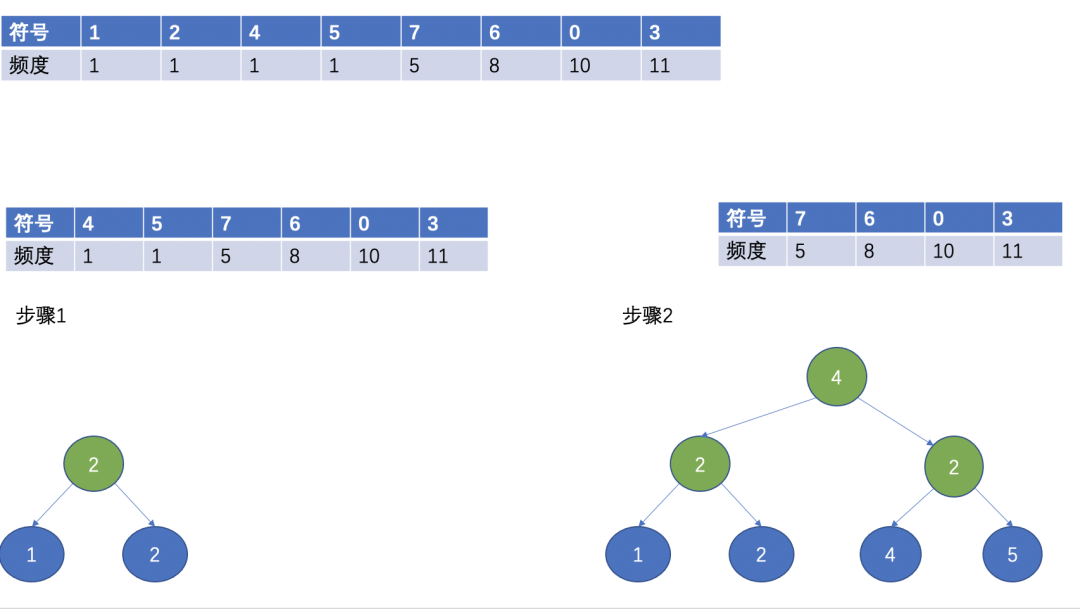
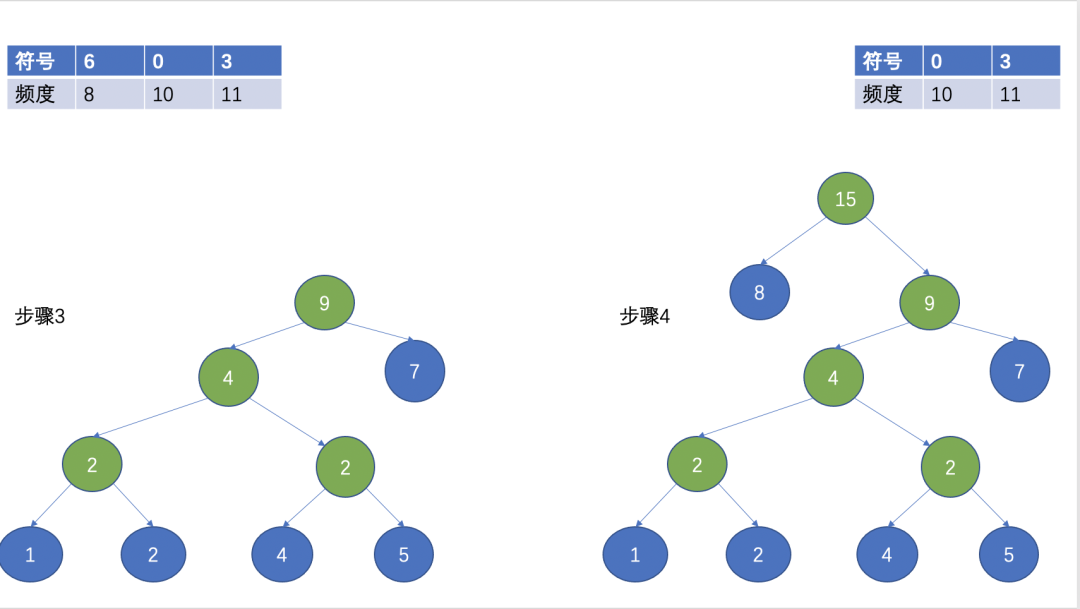
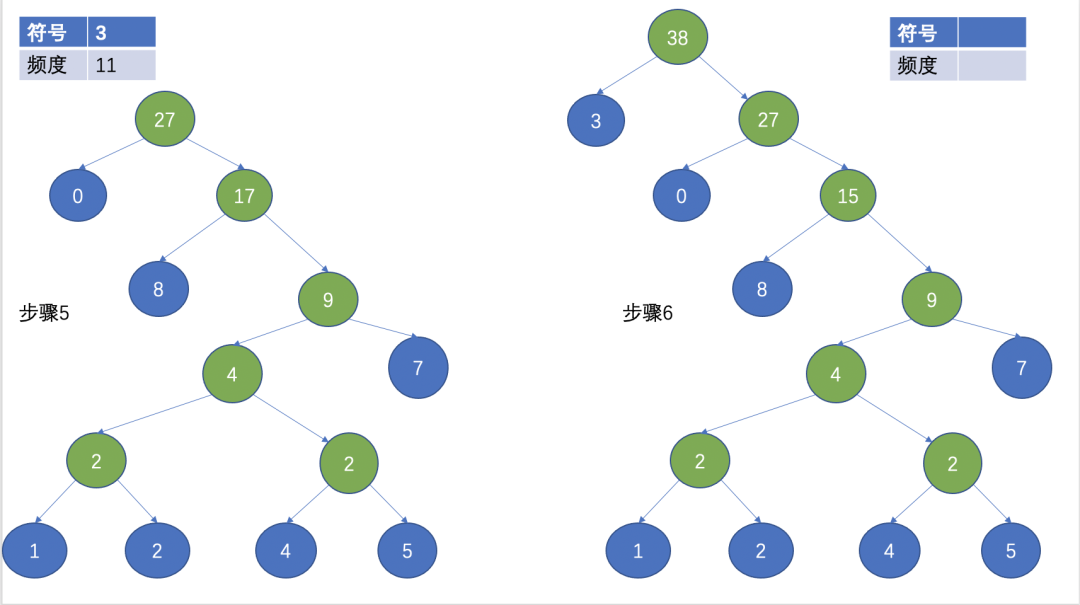
（Huffman 树）

经过上面的步骤，就形成了一颗Huffman树，Huffman编码经常用在无损压缩中，其基本思想是用短的编码表示出现频率高的字符，用长的编码来表示出现频率低的字符，这使得编码之后的字符串的平均长度、长度的期望值降低，从而实现压缩的目的。

三、故事的主角 Lepton

不完美。

上面的JPEG压缩虽然降低了图片的大小且质量良好以至于人眼很难分辨其差异，但是由于是有损的压缩，图片质量不能恢复到原来的品质，而且实际上此时的jpg图片仍有压缩空间。

Lepton便可以在JPEG基础上进一步对图片进行无损压缩。

3.1 为什么选择 Lepton

与lepton类似的压缩工具还有jpegcan，MozJPEG，PackJPG，PAQ8PX。但这些工具都或多或少有一些缺陷，使得不如lepton更加适合工业生产。

比如PackJPG需要按照全局排序的顺序重新排列文件中的所有压缩像素值。这意味着解压缩是单线程的，同时需要整个图像放入内存中导致处理图片的时延较高吞吐较低。

下图是lepton论文中对几款工具的比较：

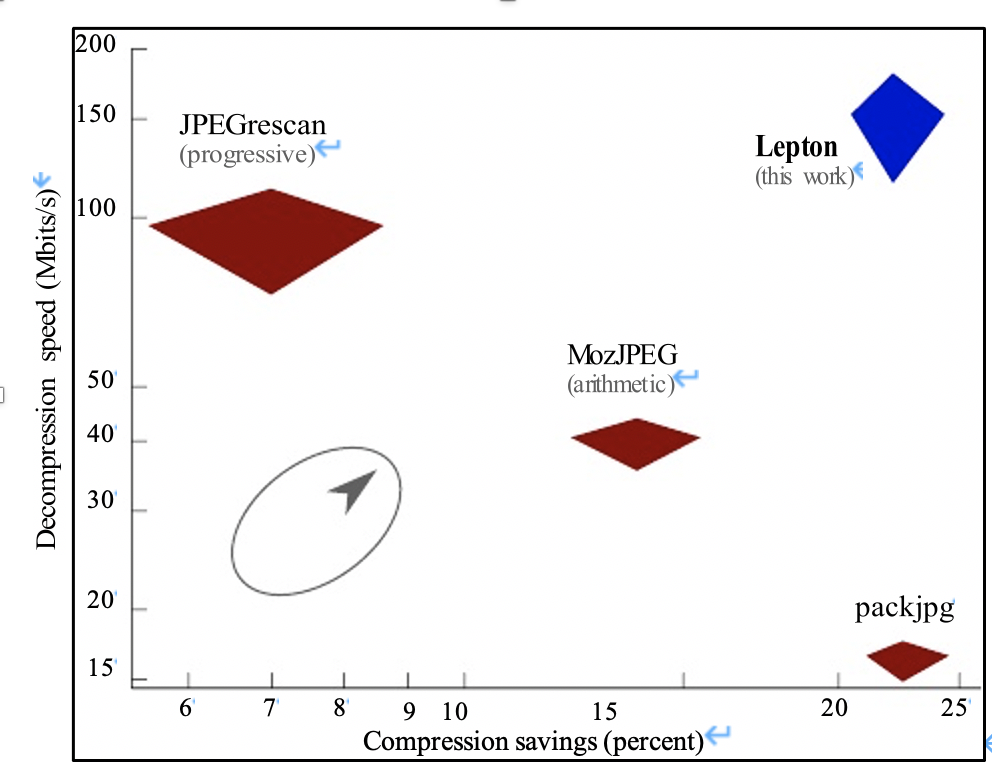
3.2  Lepton进行了哪些优化。

首先在算法上Lepton将图像分为两部分header和图片数据本身，header使用DEFLATE进行无损压缩，图片本身使用算数编码替换霍尔曼编码进行无损压缩。由于JPEG使用Huffman编码，这使得利用多线程比较困难，Lepton使用"Huffman切换词"进行了改进。

其次Lepton使用了一个复杂的自适应概率模型，这个模型是通过在大量的野外图像上进行测试而开发的。该模型的目标是对每个系数的值产生最准确的预测，从而产生更小的文件；在工程上允许多线程并发处理，允许分块跨多个服务器分布式处理，流的方式逐行处理有效的控制了内存，同时还保证了数据读取和输出的安全。

正是Lepton在上述关键问题的优化，使得它目前可以很好的在生产环境中使用。

3.3  Lepton在vivo存储中的探索

预期收益：

目前对象存储其中的一个集群大约有100PB数据，其中图片数据大概占70%, 而图片中有90%的图片都是jpeg类型图片，如果按照平均23%的压缩率，那么 100PB * 70% * 90% * 23% = 14.5PB，将实现大约14.5PB的成本节约。

同时由于是无损压缩，很好的保证了用户的使用体验。当前lepton压缩功能的设计如下图：

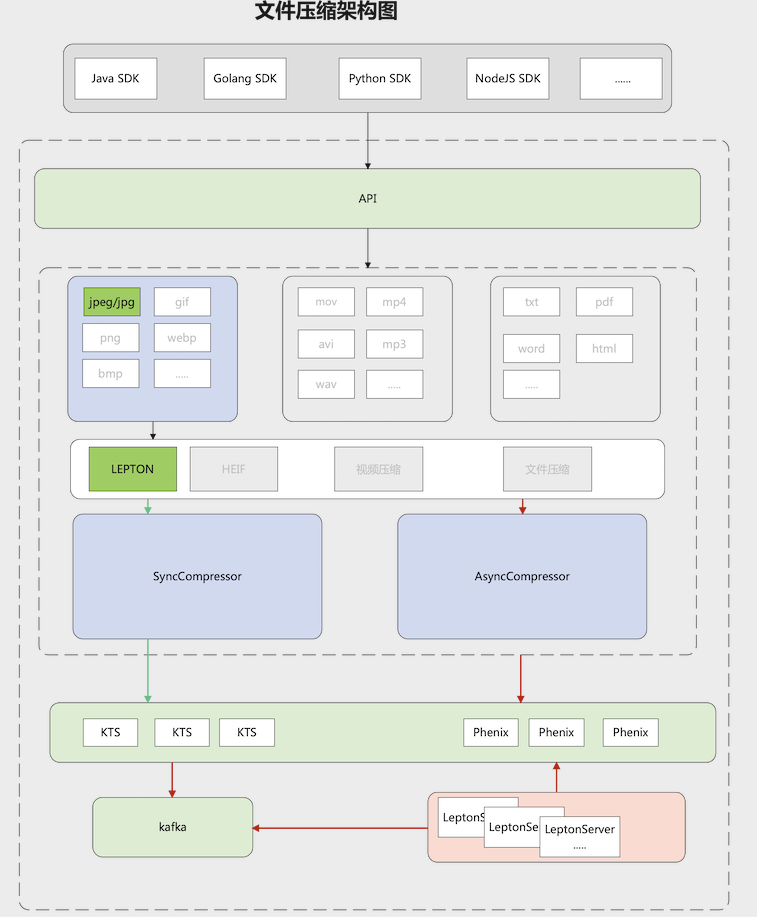
当前遇到的挑战：

1. lepton压缩与解压缩对服务器的计算性能要求较高、消耗较大。
2. 期望充分利用空闲服务器CPU资源，达到降本增效的目的。
3. 面对潮汐现象具备动态扩缩容的能力。

当前面临的主要问题：

当前大部分图片的大小在4M-5M， 经过测试对于4M-5M大小的文件压缩时延在1s左右的情况下，需要服务器至少16核心、承载5QPS。此时每个核心的利用率都在95%以上。可见 Lepton的压缩对计算性能要求很高。当前常见的解决方案是使用FPGA卡进行硬件加速、以及横向扩容大量的计算节点。FPGA的使用会增加硬件成本，降低压缩带来的成本收益。

解决方案：

为了解决上述问题及挑战，我们尝试采用物理服务器和Kubernetes混合部署的方式解决计算资源的使用和动态扩所容的问题，架构示意图如下：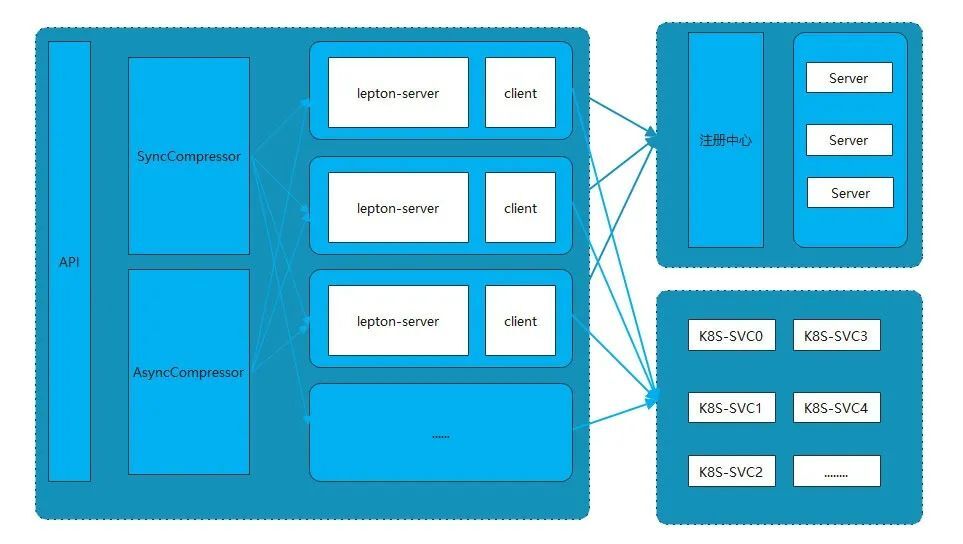

对于物理服务器的管理以及扩所容通过服务的注册于发现进行弹性扩所容、通过此cgroup/Taskset等方式对进程的cpu使用进行管理。同时对接使用Kubernetes以容器的方式进行管理、容器的灵活性更加适合这种计算型的服务。

3.4 性能评测

无论是同步压缩，还是异步压缩，通常更加关注图片读取的延时。大量的图片读取会给服务器带来较大的压力，压力主要来自于图片的解压计算。为了提高解压缩效率，以及充分利用公司的资源，我们未来将lepton压缩服务以独立的服务模式分布于cpu空闲的服务器，可以按照资源空闲程度，空闲时间，充分利用资源的峰谷来提高计算性能。

压测数据：

我们选取了不同大小的图片文件，在单机环境下进行了压缩与解压缩测试，测试结果如下图：

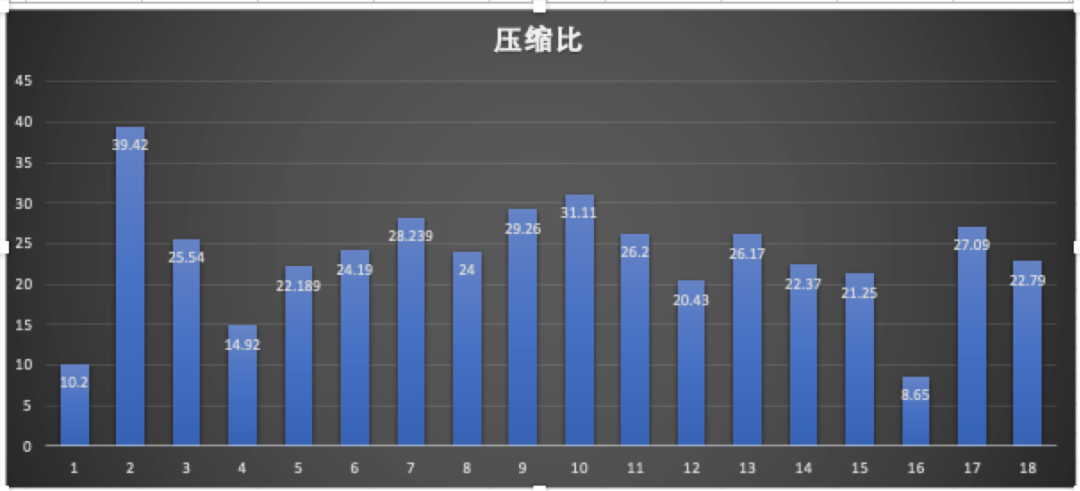
压缩比平均保持在22%左右。

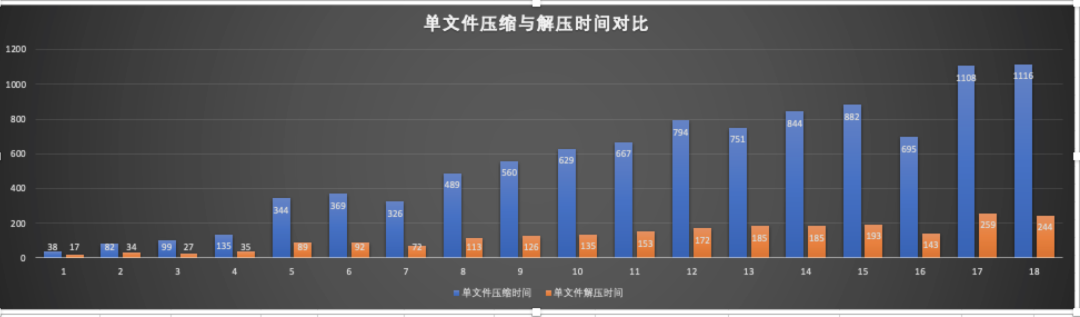
上图是不同大小的文件压缩与解压缩时间比例图，橙色是解压时间，蓝色是压缩时间。

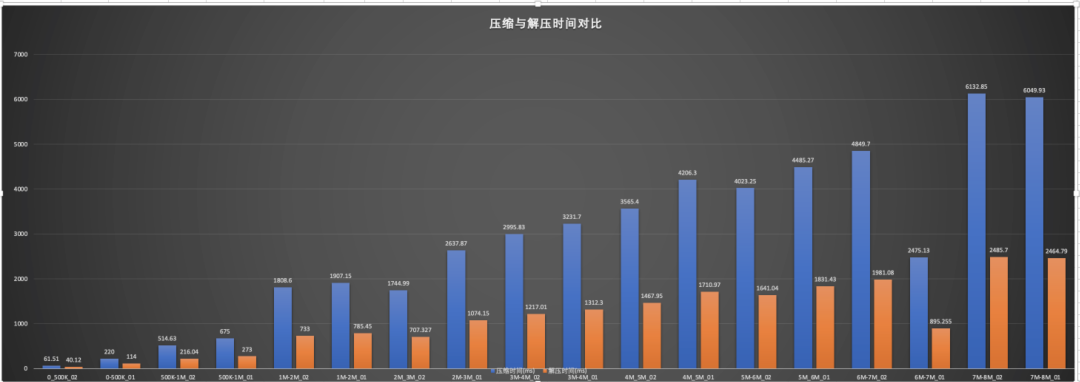
上图是不同大小的图片，在32线程并发，每个线程处理100个文件的测试数据。

四、 图片压缩的常见问题

4.1  通过文件格式区分有损和无损压缩

4.2  常见的无损压缩算法

五、 总结

Lepton的无损压缩能够提供比较高的压缩比，同时不影响用户的图片质量和使用体验、在大数据量的场景下会获得比较明显的收益。

不足之处是对计算性能要求较高、只支持jpeg类型的图片。对于性能的要求行业内也都有比较成熟的解决方案，例如上文提到的FPGA和弹性计算方案。关键在于根据企业需求选择合理的方案。

引用：

1. 《The Design, Implementation, and Deployment of a System to Transparently Compress Hundreds of Petabytes of Image Files For a File-Storage Service》
2. 《基于深度学习的JPEG图像云存储研究》
3. 《JPEG-Lepton压缩技术关键模块VLSI结构设计研究》