P1024 [NOI2001] 食物链【种类并查集】

题意

P1024

简化题意：给定 \(n\) 和 \(k(n\leqslant5\times10^4,k\leqslant10^5)\) ，表示有 \(n\) 个动物， \(k\) 个描述，其中：

\(n\) 个动物分别属于 \(A,B,C\) 中的一种，定义如 \(C\to B\to A\to C\) 的环形食物链；

\(k\) 个描述分两种：1.1 x y表示 \(x,y\) 是同类； 2. 2 x y表示 \(y\to x\) .

在 \(k\) 个描述中，有真假之分，其中假的满足：

• 与之前的真话矛盾；
• \(x\) 或 \(y\) 比 \(n\) 大；
• 同类相吃。

求出假话总数。

思路

思路启发

首先进来一组 \(x,y\) ，易得有且仅有三种有用的关系：

• \(y\) 是 \(x\) 的同类。
• \(y\to x\) ， \(y\) 是 \(x\) 的猎物；
• \(y\to x\) ， \(x\) 是 \(y\) 的天敌。（其实是与关系1是相互的）

那么，我们要维护三个逻辑关系，即有联通性，又有对立性，就要开 三元种类并查集 了。

实际上就是把一个并查集扩大三倍，在每个并查集里维护联通性，即同类关系；在三个并查集之间维护对立性，即猎物和天敌关系。

实际利用

我们可以假设：（\(B\to A\to C\to B\) ，满足题干关系就行）

• 集合\(A(1\sim n)\) 为中间者；
• 集合\(B(n+1\sim 2n)\) 为猎物；
• 集合\(C(2n+1\sim 3n)\) 为天敌；

现在的目的就是用三个集合，依次维护正确的逻辑关系，如果有假话，那么应无法在上面成立，统计无法成立的关系即可。

不妨用图模拟个样例：

点击查看样例

4 5
1 1 3
2 2 4
2 3 2
1 1 4
2 2 1

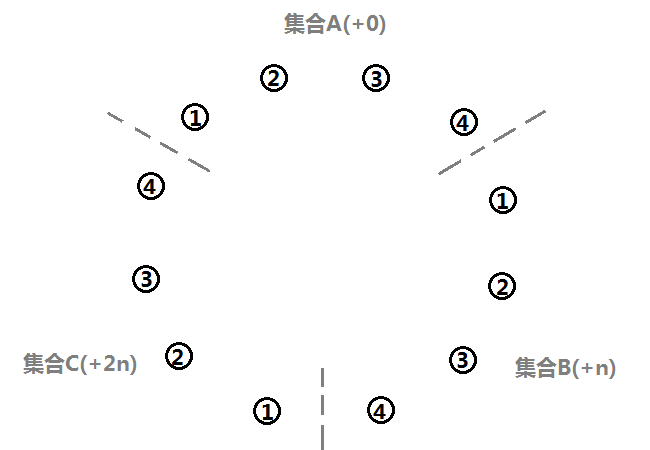
\(k_1:\) \(1\) 和 \(3\) 是同类，那么就把它俩合并到一个集合，同时注意到，都在集合\(A\) 中，则分别都会在集合\(B\) 和集合\(C\) 中，它俩同类，那它俩的猎物和天敌必定同类。

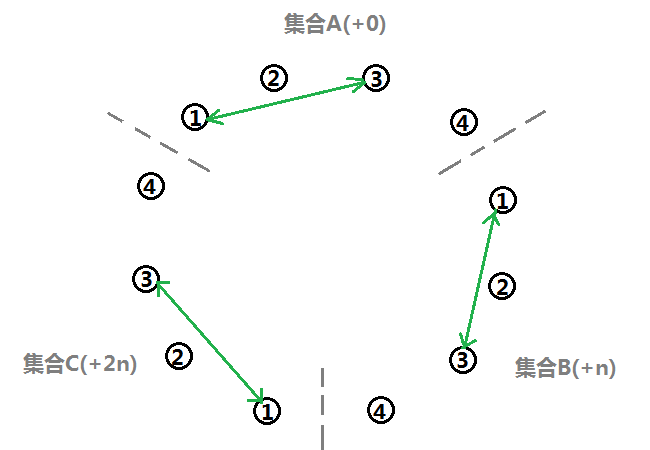
\(k_2:\) \(2\) 吃 \(4\) ，则有两个逻辑关系：

• \(4\) 是 \(2\) 的猎物，此时 \(2\) 是中间者，在集合\(A\) ，\(4\) 是猎物，在集合\(B\) ，即 \(4(B)\to2(A)\) ；
• \(2\) 是 \(4\) 的天敌，此时 \(4\) 是中间者，在集合\(A\) ，\(2\) 是天敌，在集合\(C\) ，即 \(4(A)\to2(C)\) ；

但我们观察 \(B\to^1 A\to^2 C\to^3 B\) ，关系 \(3\) 也应存在才能形成循环，即 \(4(C)\to2(B)\) ；

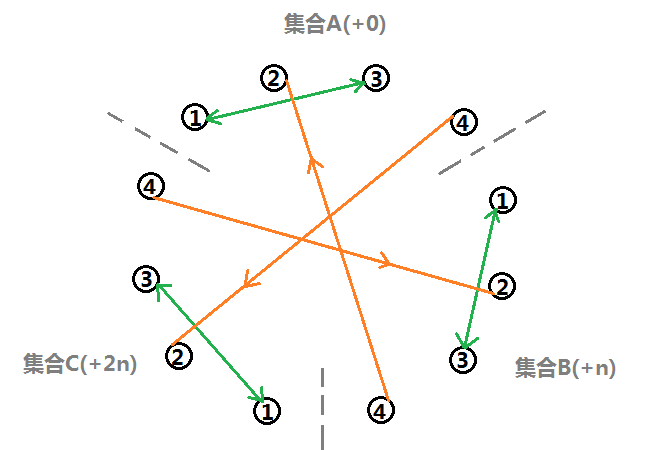
\(k_3:\) 同理。

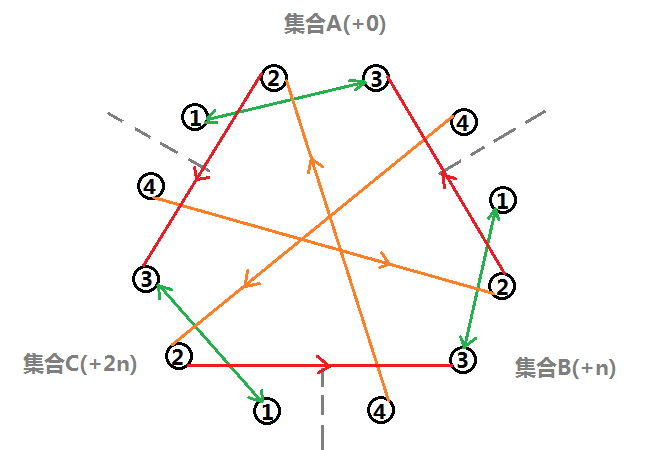
\(k_4:\) 此时 \(1\) 与 \(4\) 是同类的是假的。

判断同类是否为假，即判断是否存在 \(1\to4\) 或 \(4\to1\) 的情况，即 \(4\) 的猎物是否是 \(1\) 或 \(4\) 的天敌是否是 \(1\) 。（判断有多样，这样统一了左边的 \(1\)）

我们非别求一下对应点的根节点看看：

\(k_5:\) 此时 \(2\) 吃 \(1\) 是假的。

判断吃与被吃是否为假，即判断是否存在 \(2\) 与 \(1\) 是同类或 \(2\to1\) 的情况，即 \(2\) 和 \(1\) 是否在同一集合（此时三个集合显然是等效的）或 \(1\) 的猎物是否是 \(2\) 。

code

#include<bits/stdc++.h>
using namespace std;
const int N=5e4+10,K=1e5+10;
int n,k,fa[3*N],cnt;
int get(int x)
{
	if(fa[x]==x) return x;
	return fa[x]=get(fa[x]);
}
void merge(int x,int y)
{
	fa[get(x)]=get(y);
}
int main()
{
	cin>>n>>k;
	for(int i=1;i<=3*n;i++) fa[i]=i;
	for(int i=1;i<=k;i++)
	{
		int op,x,y;
		cin>>op>>x>>y;
		if(x>n || y>n) { cnt++; continue; }
		if(op==1)
		{
			if(get(x)==get(y+n) || get(x)==get(y+2*n)) cnt++;
			else
			{
				merge(x,y);
				merge(x+n,y+n);
				merge(x+2*n,y+2*n);
			}
		}
		else
		{
			if(get(x)==get(y) || get(x)==get(y+n)) cnt++;
			else
			{
				merge(x,y+2*n);
				merge(x+n,y);
				merge(x+2*n,y+n);
			}
		}
	}
	cout<<cnt<<endl;
	return 0;
}

总结

种类并查集不仅可以维护联通性，也可以维护对立性。