【补题】第 46 届 ICPC EC Final

比赛

题目：第 46 届 ICPC EC Final（正式赛）

榜单

A. DFS Order

签到题

容易发现对于一个点，它的最小位置就是从根走一条链直接到它，最大位置就是除了它的子树，其它全已经走过了。

\[minpos=depth[i] , maxpos=n-size[i]+1
\]

其中\(depth[i]\)表示结点\(i\)的深度，\(size[i]\)表示以结点\(i\)为根的子树大小。

代码：

点击查看代码

#include<cstdio>
#include<cstdlib>
#define maxn 100010
using namespace std;
int deep[maxn],sz[maxn];
int fst[maxn],to[maxn<<1],nxt[maxn<<1],cnt=0;
void add(int x,int y){
    to[++cnt]=y;
    nxt[cnt]=fst[x];
    fst[x]=cnt;
}
void dfs(int x,int fa){
    int i;
    deep[x]=deep[fa]+1;
    sz[x]=1;
    for(i=fst[x];i;i=nxt[i]){
        if(to[i]==fa) continue;
        dfs(to[i],x);
        sz[x]+=sz[to[i]];
    }
    return;
}
int main(){
    int i,j,T,n,x,y;
    scanf("%d",&T);
    while(T--){
        cnt=0;
        scanf("%d",&n);
        for(i=1;i<=n;++i) fst[i]=0;
        for(i=1;i<n;++i){
            scanf("%d%d",&x,&y);
            add(x,y);add(y,x);
        }
        dfs(1,0);
        for(i=1;i<=n;++i){
            printf("%d %d\n",deep[i],n-sz[i]+1);
        }
    }
    // system("pause");
    return 0;
}

I. Future Coder

签到题+1

这个式子\(a_i*a_j<a_i+a_j\)很难看，所以我们把它变成\((a_i-1)*(a_j-1)<1\)

方便起见我们读入之后直接把\(a\)数组每个元素全部\(-1\)，于是要求\(a_i*a_j<1\)的数对有多少。

然后就简单了，考虑到都是整数，有\(a_i*a_j\leq 0\)，于是对于后缀统计一下正数负数和\(0\)的数量就行。

代码：

点击查看代码

#include<cstdio>
#include<cstdlib>
#define maxn 1000010
#define ll long long
using namespace std;
int a[maxn],pre_neg[maxn],pre_zero[maxn];
void solve(){
    int n,i,j;
    ll sum=0;
    scanf("%d",&n);
    for(i=1;i<=n;++i) scanf("%d",&a[i]);
    for(i=1;i<=n;++i) a[i]--;
    for(i=1;i<=n;++i){
        pre_neg[i]=pre_neg[i-1]+(a[i]<0),pre_zero[i]=pre_zero[i-1]+(a[i]==0);
    }
    for(i=1;i<=n;++i){
        int neg=pre_neg[n]-pre_neg[i],zero=pre_zero[n]-pre_zero[i];
        int pos=n-i-neg-zero;
        if(a[i]>0) sum+=zero+neg;
        else if(a[i]==0) sum+=n-i;
        else sum+=zero+pos;
    }
    printf("%lld\n",sum);
    return;
}
int main(){
    int i,j,T,n,x,y;
    scanf("%d",&T);
    while(T--){
        solve();
    }
    // system("pause");
    return 0;
}

L. Fenwick Tree

简单题，但需要一点思维

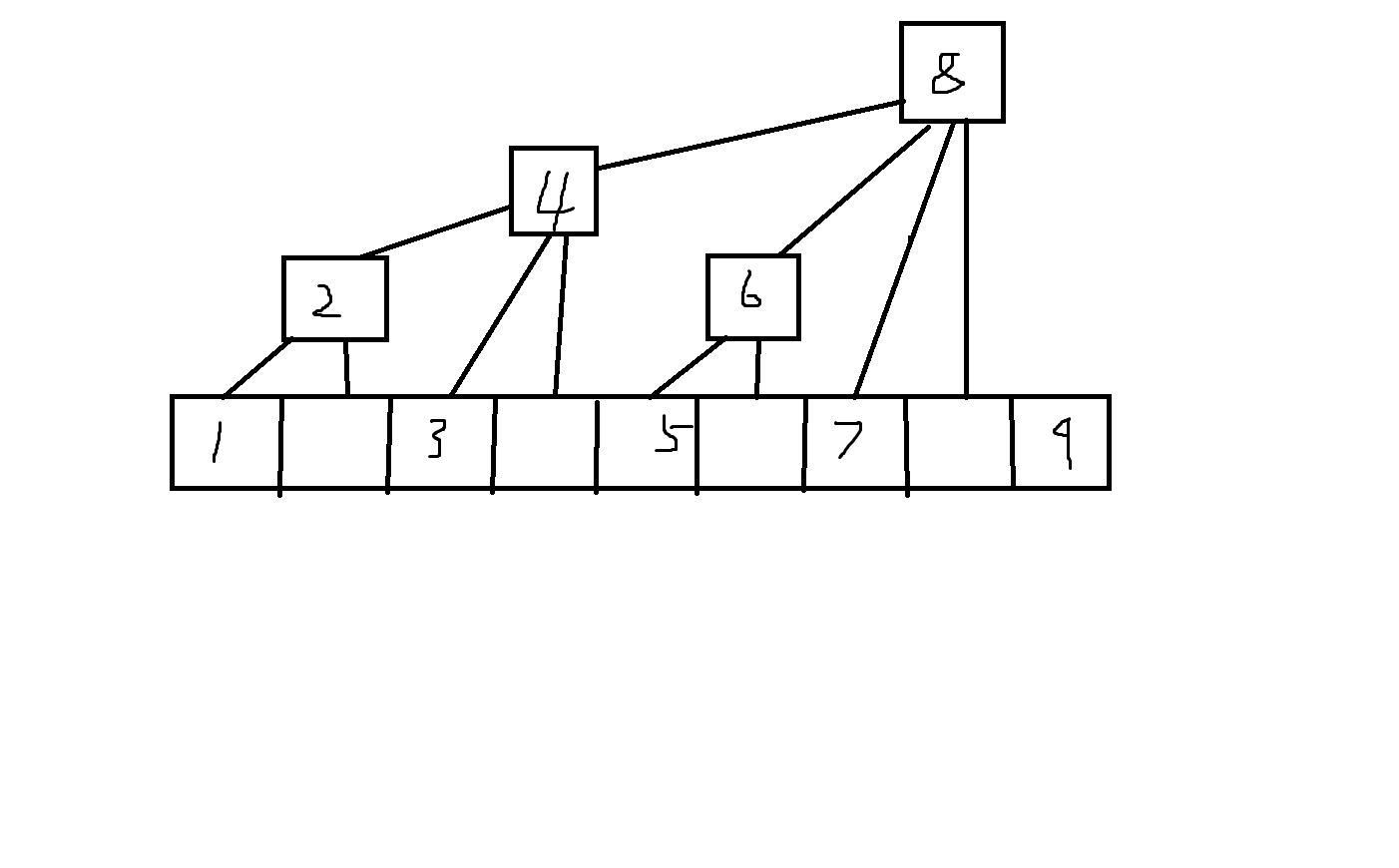
我们搭出一个树状数组，考虑树状数组的update函数是沿怎样的路径更新的：

手玩一下就会发现，\(update\)函数相当于对从树根到\(i\)这条路径做了区间加（\(val\)值任意实数）。

注意一点，如果\(j\)是\(i\)的祖先，那么以\(i\)为根的子树内部的所有update操作对\(i\)和\(j\)的影响是一样的。

接着我们从底向上考虑，首先叶子如果是\(0\)，必然啥都不干；叶子是\(1\)，有一个从根到叶区间加，\(ans++\)，同时发现这一操作影响到了该叶子的父节点，

我们把父节点的\(a[fa]\)标记加一，表示对于\(fa\)节点，多了一个影响它的子树。

再考虑中层节点，如果节点\(x\)对应的

\(c[x]==1\)，且\(a[x]==0\)，说明它的子树没影响它，需要进行\(x\)到根的区间加，\(ans++\)。

\(c[x]==1\)，且\(a[x]>0\)，说明有一个或多个子树中的操作对它有影响，那么必然可以调整每个操作的\(val\)值使得它们和非零，\(ans\)不变。

\(c[x]==0\)，且\(a[x]==0\)，啥都不用干，\(ans\)不变。

\(c[x]==0\)，且\(a[x]>0\)，这就有点意思了，要分类讨论下。直接上结论，当且仅当\(a[x]==1\)时我们需要一次\(x\)到根的区间加把它变回去，\(ans++\)。

（其实也好想，只要\(a[x]>=2\)就能调整\(val\)使得对\(x\)的影响之和为\(0\)）。

代码：

点击查看代码

#include<cstdio>
#include<cstdlib>
#define maxn 100010
using namespace std;
char s[maxn];
int a[maxn];
int lowbit(int x){
    return x&(-x);
}
void solve(){
    int n,i,j,ans=0;
    scanf("%d%s",&n,s+1);
    for(i=1;i<=n;++i) a[i]=0;
    for(i=1;i<=n;i<<=1){
        for(j=i;j<=n;j+=(i<<1)){
            if(s[j]-'0'){
                if(j+lowbit(j)<=n) a[j+lowbit(j)]++;
                if(!a[j]){
                    ans++;
                }
            }
            else{
                if(a[j]==1){
                    ans++;
                }
            }
        }
    }
    printf("%d\n",ans);
    return;
}
int main(){
    int i,j,n,m,T;
    scanf("%d",&T);
    while(T--){
        solve();
    }
    return 0;
}