图与网络分析—R实现（三）

最小生成树 (Minimum Spanning Tree) 应该大家都不陌生，Spanning 有跨越的意思，生成树一般来说每个节点都能访问到别的节点，是一个连通树。所以，一般考虑无向图里去造生成树。生成树又分最小和最大两种，其中最小生成树应用比较多。

一、最小生成树问题

生成树：一个连通图的生成树是指一个连通子图，它含有图中全部n个顶点，但只有足以构成一棵树的n-1条边。一颗有n个顶点的生成树有且仅有n-1条边，如果生成树中再添加一条边，则必定成环。

最小生成树：在连通网的所有生成树中，所有边的代价和最小的生成树，称为最小生成树。

二、求最小生成树算法

2.1 Kruskal算法

此算法可以称为“加边法”，初始最小生成树边数为0，每迭代一次就选择一条满足条件的最小代价边，加入到最小生成树的边集合里。

把图中的所有边按代价从小到大排序；
把图中的n个顶点看成独立的n棵树组成的森林；
按权值从小到大选择边，所选的边连接的两个顶点ui,viui,vi,应属于两颗不同的树，则成为最小生成树的一条边，并将这两颗树合并作为一颗树。
重复(3),直到所有顶点都在一颗树内或者有n-1条边为止。

2.2 Prim算法

此算法可以称为“加点法”，每次迭代选择代价最小的边对应的点，加入到最小生成树中。算法从某一个顶点s开始，逐渐长大覆盖整个连通网的所有顶点。

图的所有顶点集合为VV；初始令集合u={s},v=V−uu={s},v=V−u;

在两个集合u,vu,v能够组成的边中，选择一条代价最小的边(u0,v0)(u0,v0)，加入到最小生成树中，并把v0v0并入到集合u中。

重复上述步骤，直到最小生成树有n-1条边或者n个顶点为止。

三、最小生成树R程序

library("igraph")

#赋权图的构建

A = matrix(c(0, 0, 11, 5, 0, 0,0, 0, 9, 13, 0, 0,11, 9, 0, 9, 7, 0,5, 13, 9, 0, 15, 5,0, 0, 7, 15, 0, 9,0, 0, 0, 5, 9, 0),

           nrow= 6 , ncol= 6  ,byrow = TRUE)

g<- graph.adjacency(A,weighted=TRUE, mode = c("undirected"))

#最小生成树的计算

tr= minimum.spanning.tree(g,weights = graph_attr(g,'weight'))

plot(tr,layout=layout.reingold.tilford,edge.label=E(tr)$weight)

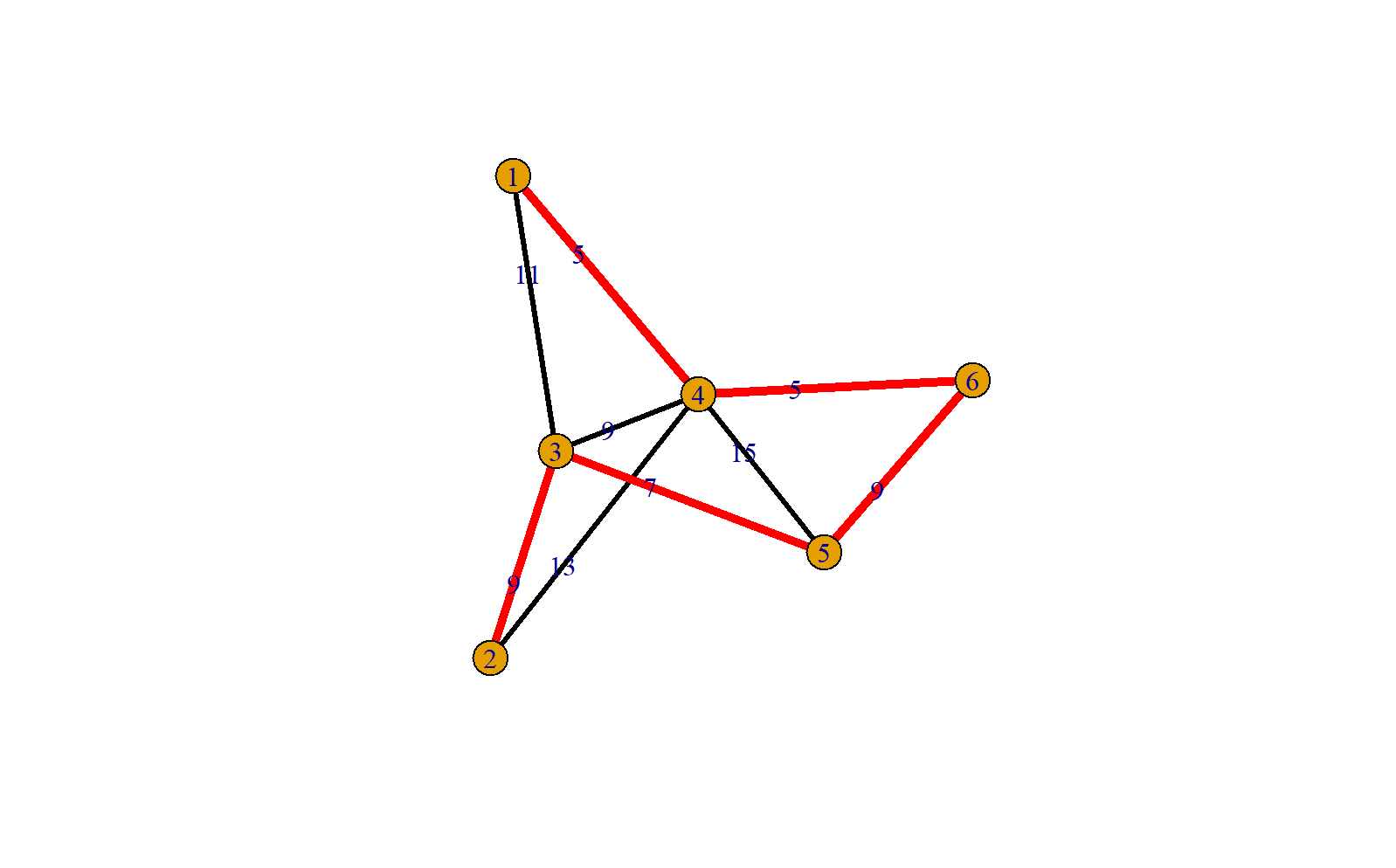
四、最小生成树合成图

library(dplyr)

ggg=get.data.frame(g)

tr1=get.data.frame(tr)

dd1=setdiff(ggg,tr1)

dd1$color="black"

dd1$width=3

tr1$color="red"

tr1$width=5

ee=union_all(dd1,tr1)

g <- make_graph(t(ee[,1:2]),directed = FALSE)

plot(g,edge.label = ee$weight,edge.color = ee$color,edge.width=ee$width)

五、最小生成树问题的应用

网络G表示n各城市之间的通信线路网线路（其中顶点表示城市，边表示两个城市之间的通信线路，边上的权值表示线路的长度或造价。可通过求该网络的最小生成树达到求解通信线路或总代价最小的最佳方案。再如（1）解决矿井通风管道设计问题；（2）几个城市之间怎么修路，可以使整体上路最短？（3）城市输水、煤气管道的优化。

参考文献

[最小生成树的两种方法（Kruskal算法和Prim算法）]（https://blog.csdn.net/a2392008643/article/details/81781766/）