[最短路径问题]Dijkstra算法(含还原具体路径)

前言

在本篇文章中，我将介绍 Dijkstra 算法解决 单源最短路径问题 ，同时还包含了具体路径的还原。以下是我自己的全部学习过程与思考，参考书籍为 《数据结构》(C++语言版) 邓俊辉 编著 。

(本文作者： Amαdeus，未经允许不得转载哦。)

---

最短路径问题

最短路径概述

在当今这个繁华的时代，我们时时刻刻生活在一张庞大的城市网络中，我们也许会想着从温暖的家乡奔向自己未来奋斗的都市，抑或是梦想着逃离城市的喧嚣去往那片心中的静谧之地......然而我们始终离不开一个问题————我们如何更快地、更短距离地前往我们所规划的目的地呢? 在这个时候，人们通常会规划好到达目的地的最佳路线，这其实就是最短路径问题在实际生活中的一个简单应用。

最短路径问题 : 给定一个带权有向图 G = (V, E, W)，同时给定一个源点 u (u ∈ V)，我们要找出从源点 u 出发到其它各点的最短路径距离，并得出这些最短路径的具体路径有哪些边构成。

其实我们要求的就是从 源点 u 出发到 其它各点 的最短路径所组成的路线网络，也就是一个 最短路径树。

最短路径示例

我们以下面这个带权有向图为示例

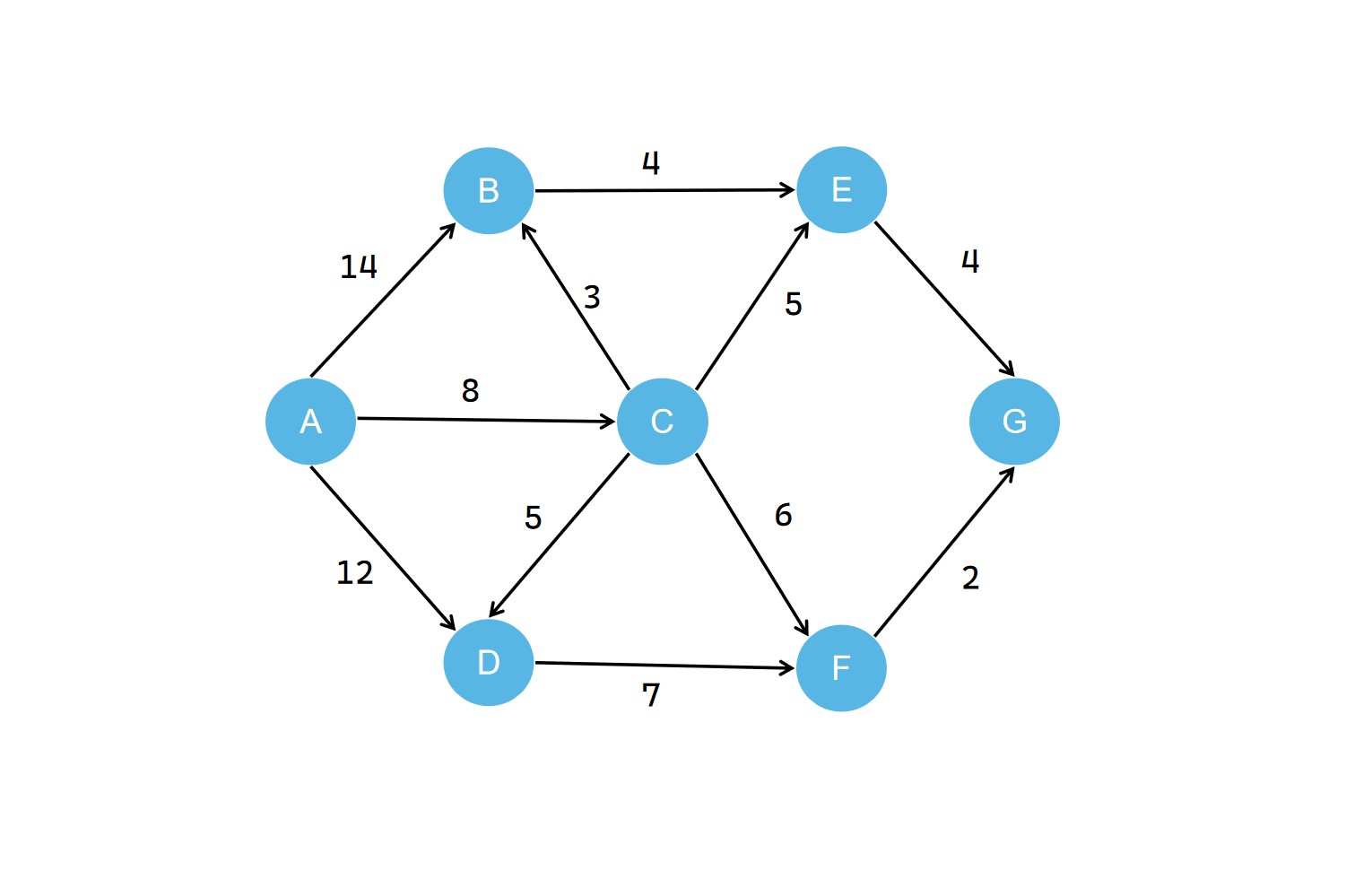
我们若以 A 为源点，得到如下的最短路径

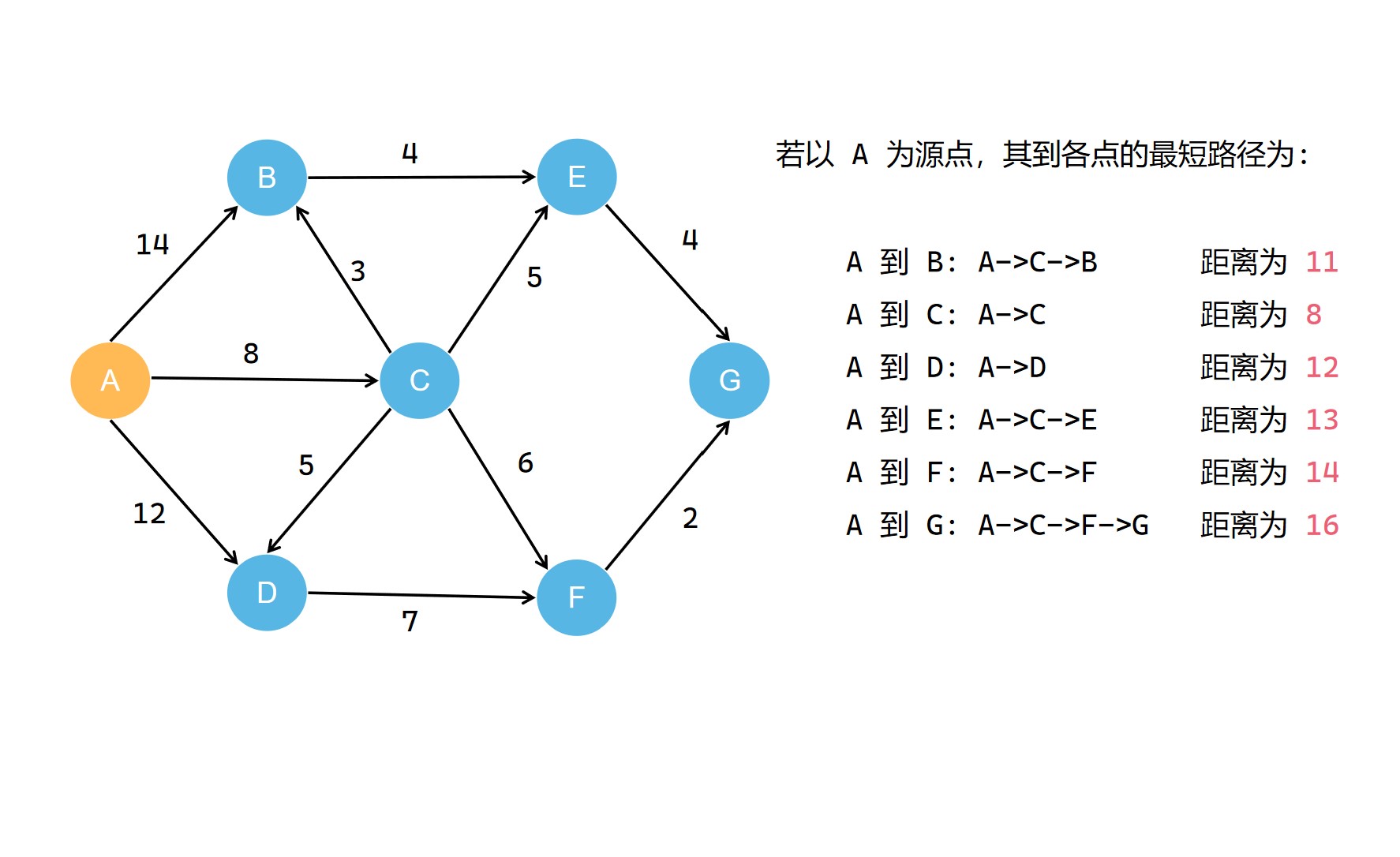
我们可以把源点到各点最短路径用绿色标记一下

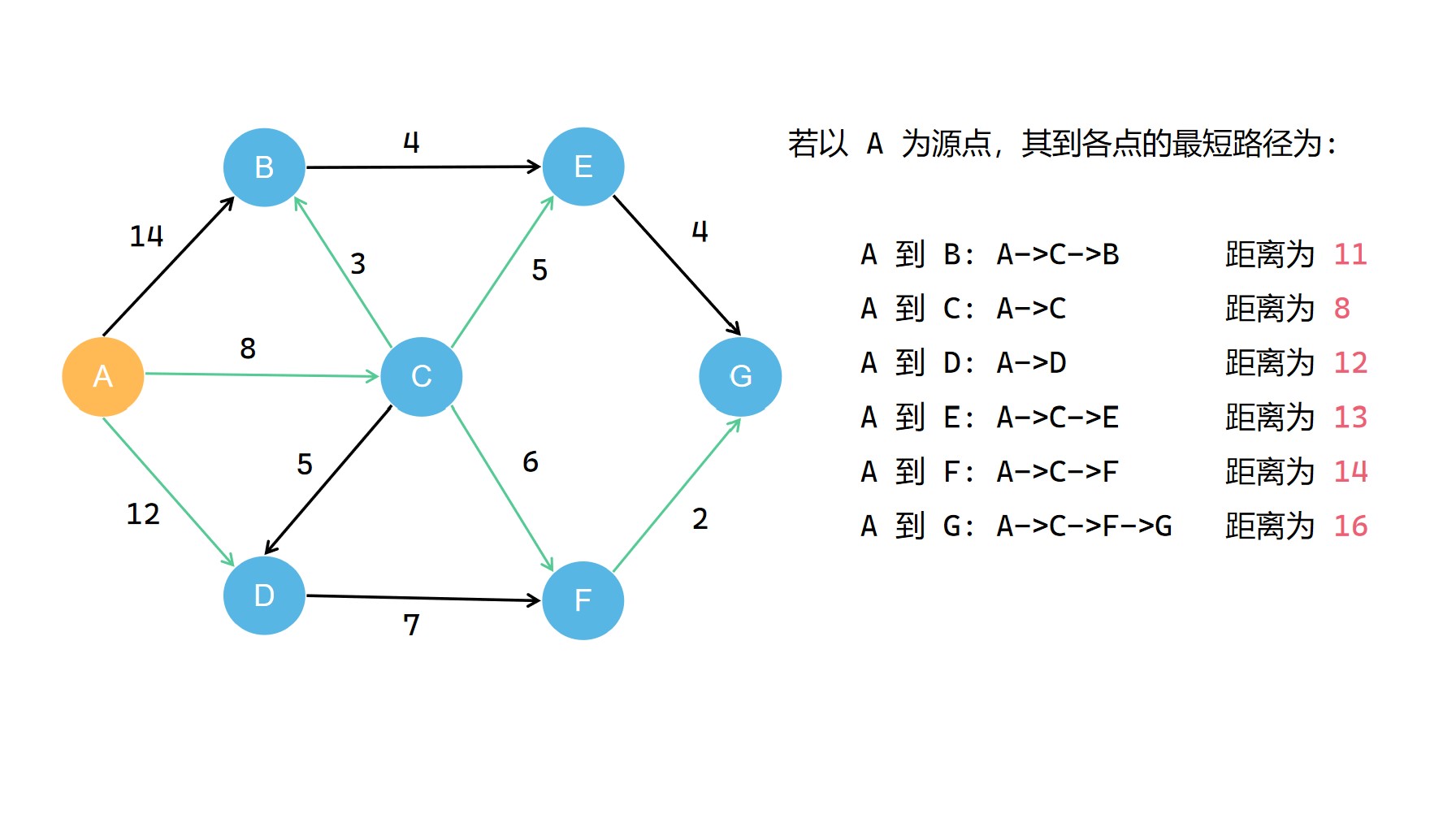
我们可以看出所有的最短路径构成了一个最短路径树

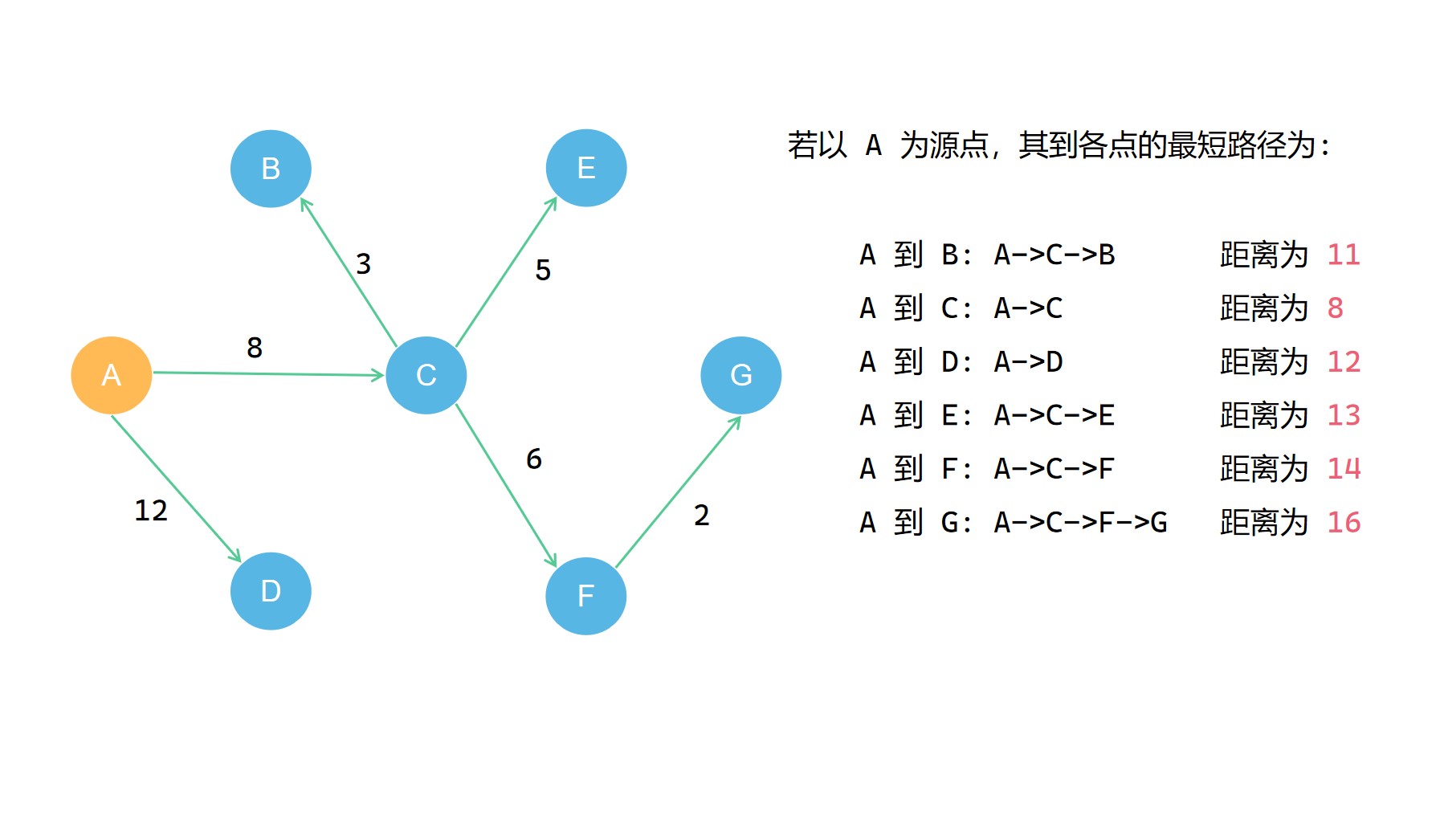
我们要求的从 源点 到 其它各点 的最短路径所组成的路线网络，就是这个最短路径树。

最短路径树性质

单调性

在上面的图中，我们不难发现，当我们确定了源点 u 到某个其它的点 v 的最短路径时，在这个最短路径的具体路线中，若有一个中转点 t，那么在这个最短路径中从源点 u 到 t 的路径也一定是 u 到 t 的最短路径(之一)。也就是说，假设源点 u 到 v 的最短路径为 p，那么p任意的前缀路径 q 一定是最优的(最短路径之一)。如果 q 不是最优的，那么就会存在另一个更短的路径比 p 更短。

这个性质还是很重要的，是解决单源最短路径问题的核心

我们画个图来理解一下

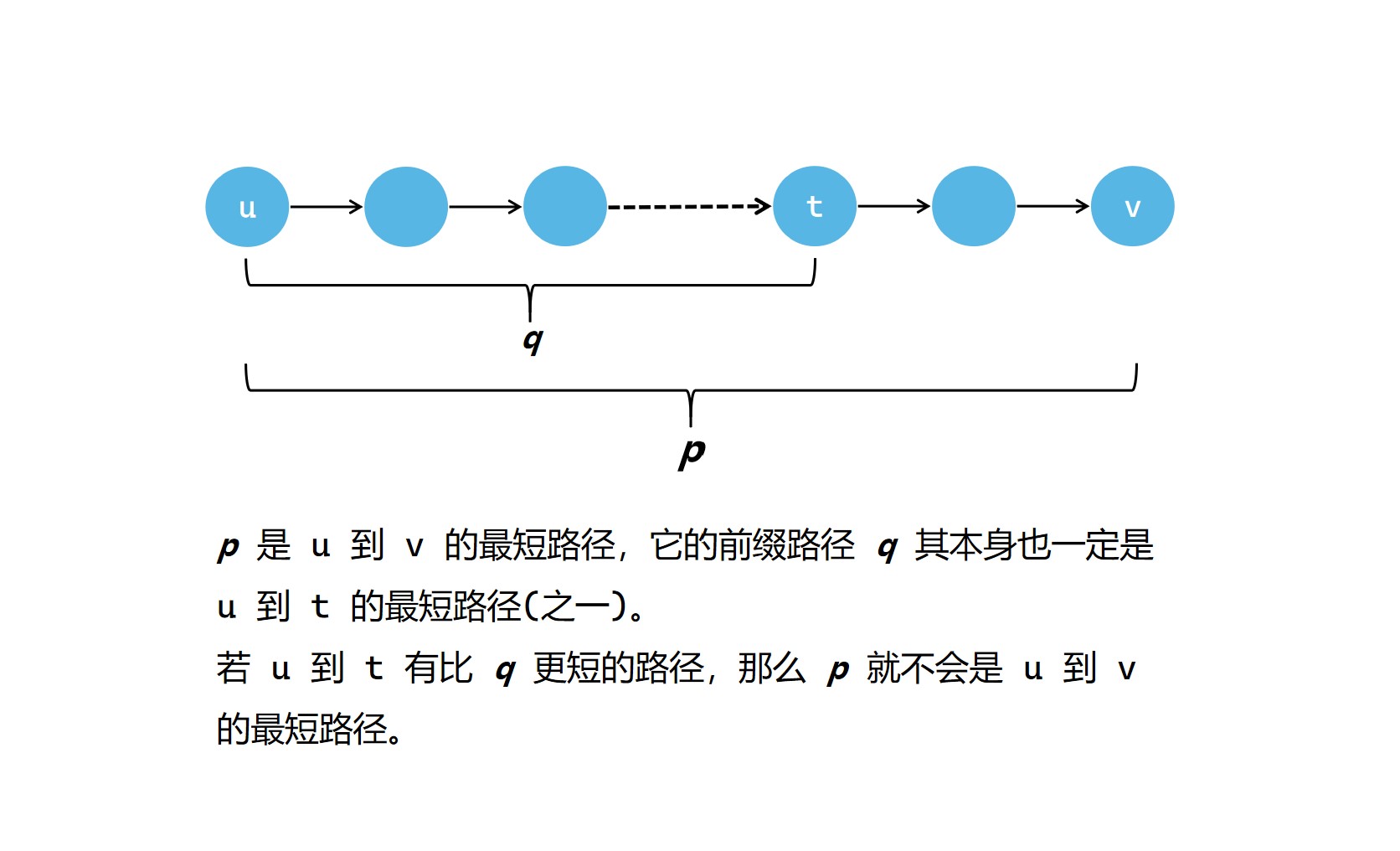
歧义性

在上面的阐述中也稍微提到一点，就是最短路径其实不一定是唯一的，有可能存在两个路径，它们的路径距离一样且都是最短的，那么此时我们二选其一就可以啦。还有一个问题就是，我们的边权都应当是正数，如果边权存在非正数，那么我们是无法定义这个图中的最短路径的(距离确实不能是非正数呀，除了自己到自己)。

无环性

这个性质其实很好理解，既然我们得到的所有最短路径构成的是一个 最短路径树，那么作为一个树，它必不会存在环。也可以由之前的 单调性 得出这个性质。

---

Dijkstra算法

算法简介

Dijkstra 算法是由荷兰计算机科学家 Edsger Wybe Dijkstra 在1956年提出的，一般解决的是 带权有向图 的 单源最短路径问题。

接下来介绍如何用 Dijkstra 算法求解 单源最短路径问题。

算法思路

Dijkstra 算法将会充分利用 最短路径树 的 单调性 这一性质。先定下源点 u，然后采用 贪心 的策略，不断去访问与源点 u 相接且之前未被访问过的最近的顶点 v(这句话里相接的意思是指可以从 u 到达 v)，使得当前的最短路径树得到扩充，一直到所有顶点都在当前的最短路径树中，那么就得到了源点 u 到其他所有顶点 v 的最短路径。

我们将当前最短路径树所有的顶点所构成的集合称为 集合S，而不在当前最短路径树中的顶点所构成的集合称为集合V-S。

算法步骤

1、首先需要定义一个辅助数组 flag[]，用于标记每个顶点是否处于当前的 最短路径树 中，后续我们将 最短路径树 称为 集合S。在初始情况下，我们会先将源点 u 划入 集合S;

2、然后我们需要再定义一个数组 dist[]，用于记录当前从源点 u 到 v (v∈V-S)的最短路径距离，比如dist[vi]就表示 u 到 vi 的当前最短路径距离。

集合S每一次扩充都需要选择当前不在集合S中且到源点 u 最短距离的顶点 t 作为扩充点，并且将其划入集合S。之后的扩充操作中，就以这个 t 作为中转点对 dist[v] 进行更新，使其记录的距离减小。在不断扩充集合S的过程中，dist[v]的记录的距离大小不断减小(可能不变)，直到最后，其记录的便是整个图中u 到 v* 的最短的距离；

另外，一开始我们要先初始化源点 u 到其邻接的顶点的距离。

3、为了还原具体路径，我们还需要一个辅助数组 pre[]，用于记录最短路径中每个顶点的前驱顶点。比如 pre[v]，其记录的是 u 到 v 的最短路径中，顶点 v 的前驱顶点。在不断扩充集合S的过程中，如果可以借助当前的扩充点 t 到达 v 的距离更短，我们也要更新 v 的前驱为 t，即 pre[v] = t 。

同样的，我们也要初始化源点 u 为其每个邻接顶点的前驱。

动态演示

(1)

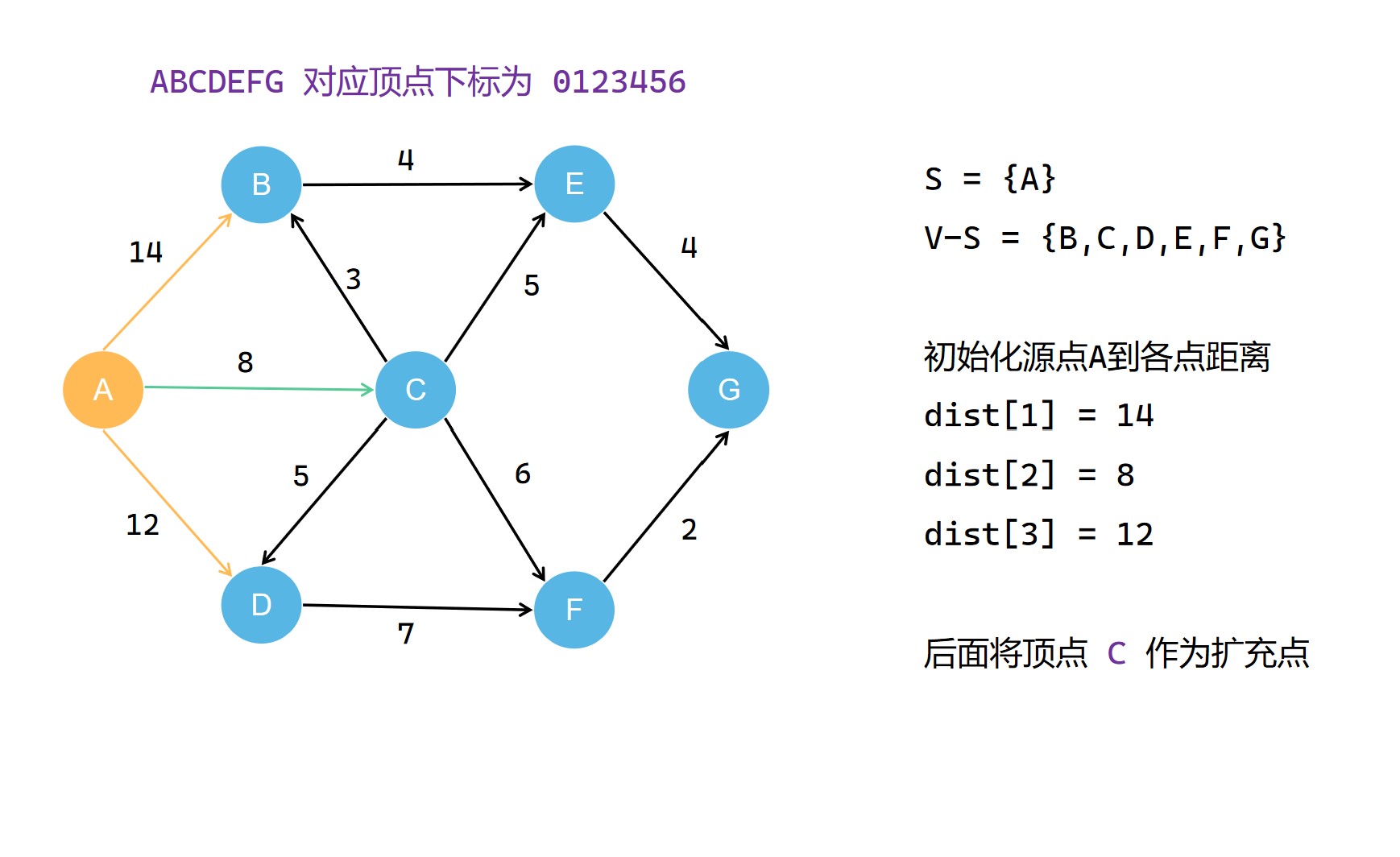
(2)

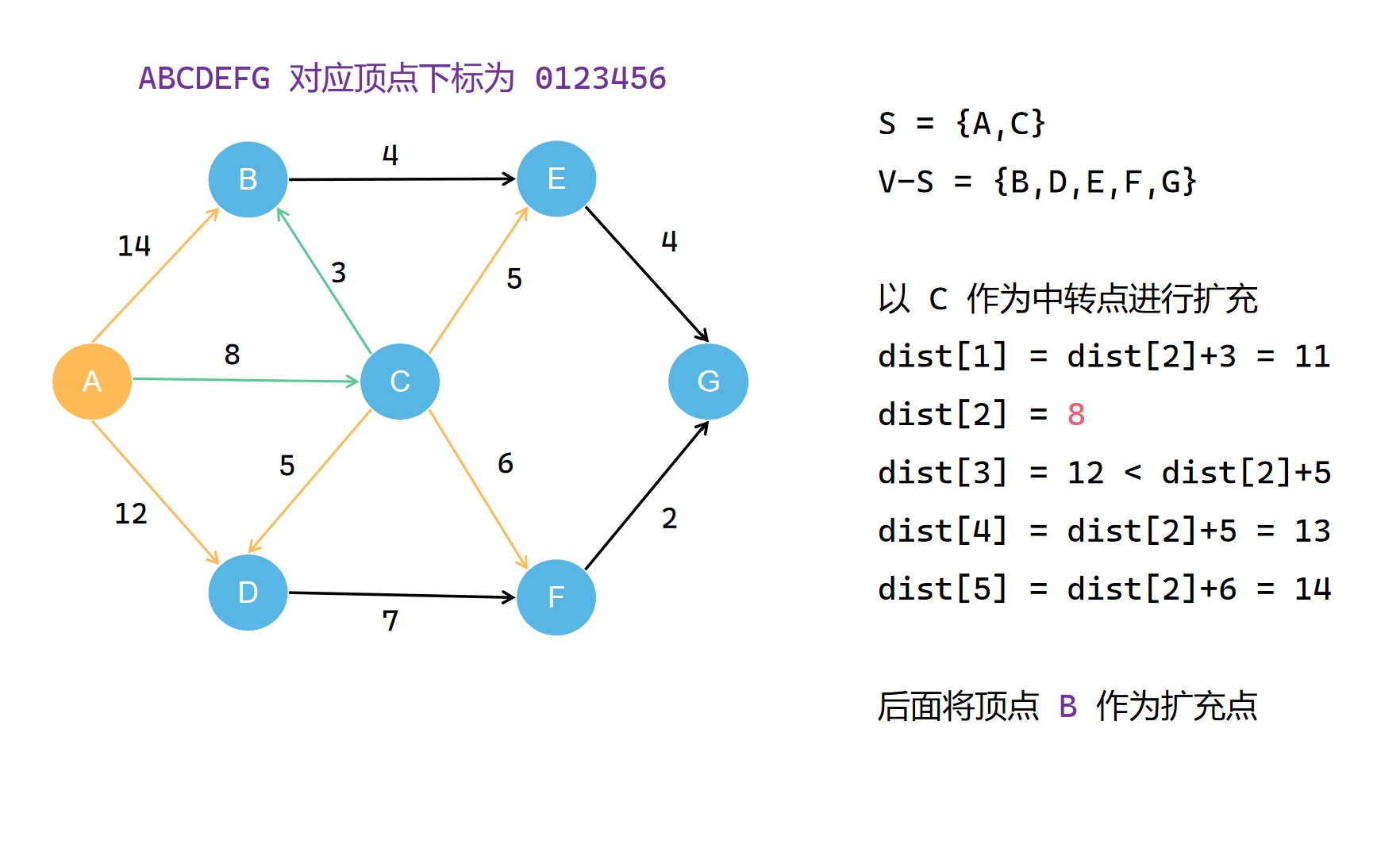
(3)

(4)

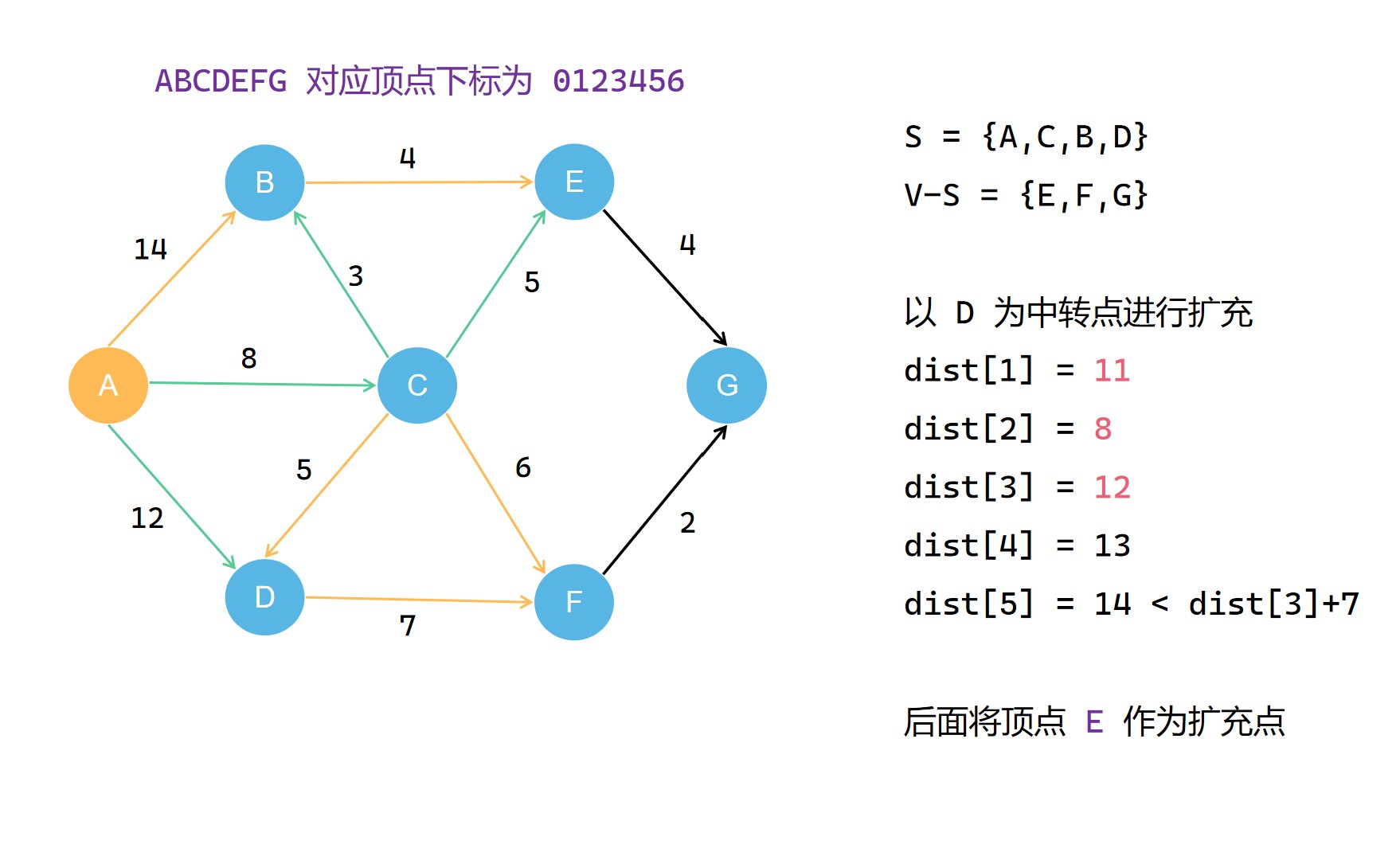
(5)

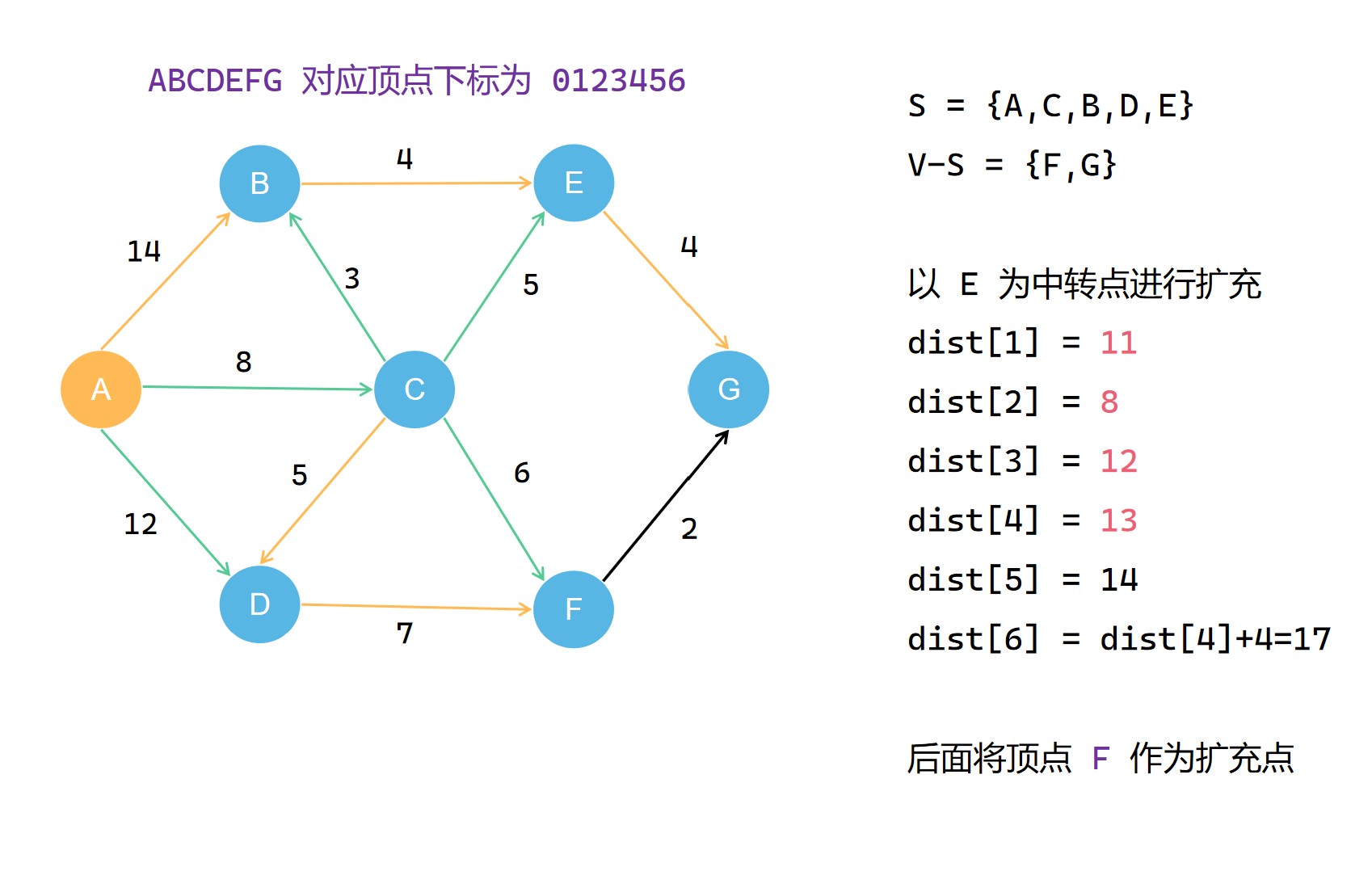
(6)

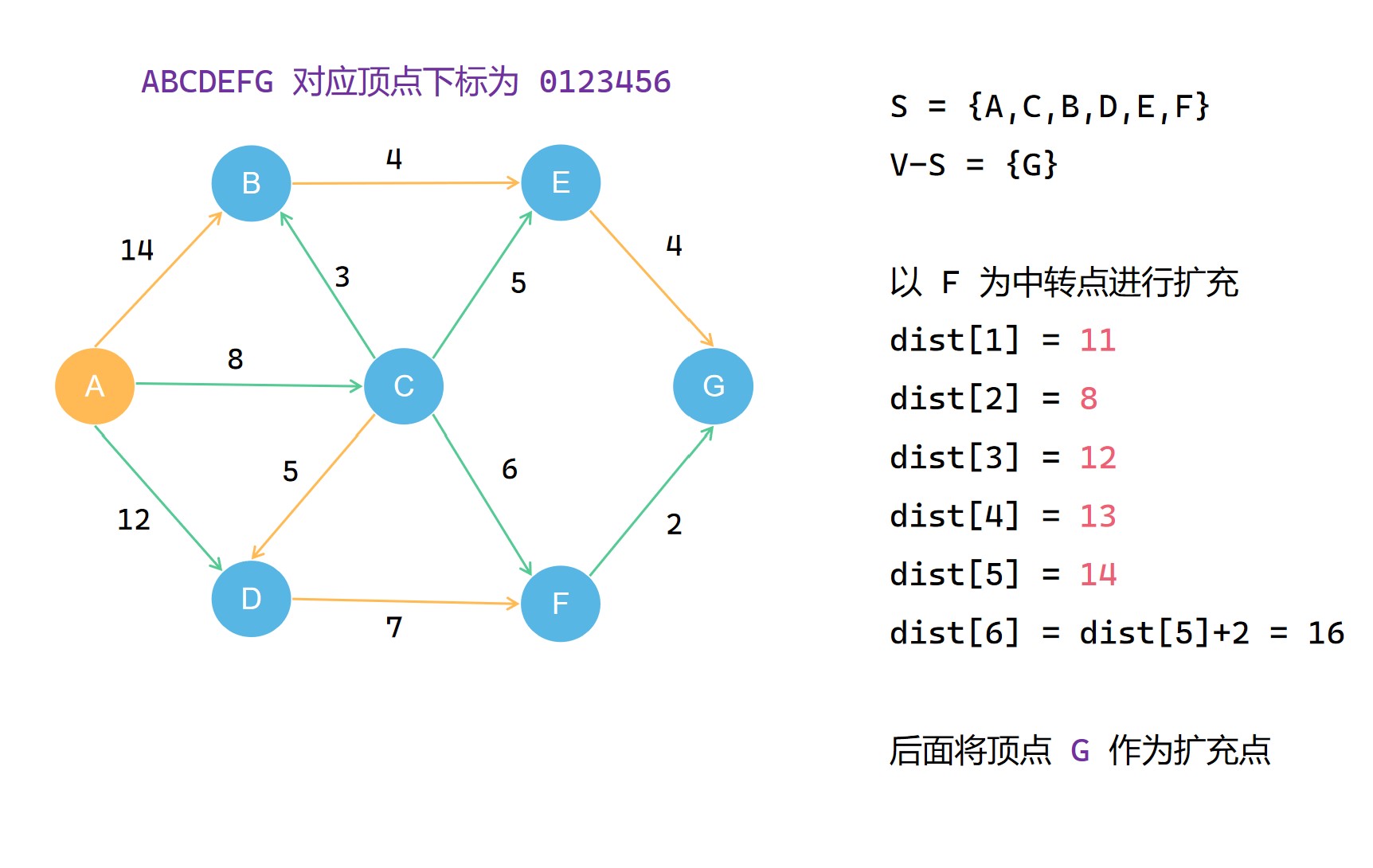
(7)

---

程序实现

以下程序是基于 图的邻接矩阵 实现的，如果不了解的话，可以先去康康别的大佬有关邻接矩阵构建图的文章哦

Dijkstra核心代码

//距离记录数组 , 前驱数组
int dist[MAX], pre[MAX];
//集合S标记数组。如果flag[i]=true,说明该顶点i已经加入到集合S(最短路径集合);否则i属于集合V-S
bool flag[MAX];            

void Dijkstra(Graph *G, int u){
    for(int v = 0; v < G->nodenums; v++){
	dist[v] = G->edge[u][v];  //初始化源点u到各邻接点v的距离
	flag[v] = false;
	if(dist[v] != INF)
	    pre[v] = u;           //若有邻接边,顶点v有前驱顶点u
	else
	    pre[v] = -1;          //若没有,先初始化为-1
    }
    flag[u] = true;               //初始化集合S,只有一个元素: 源点u
    dist[u] = 0;                  //初始化源点u到自己的最短路径为0

    /*   在集合V-S中寻找距离源点u最近的顶点t,使当前最短路径树最优  */
    for(int i = 0; i < G->nodenums; i++){
    	int tmp = INF, t = u;
    	for(int v = 0; v < G->nodenums; v++){
    	    if(!flag[v] && dist[v] < tmp){
    		//不在集合S中 并且 更小距离
    		t = v;            //记录在V-S中距离源点u最近的顶点v
    		tmp = dist[v];
    	    }
    	}

    	if(t == u)
    	    return;               //未找到直接终止
    	flag[t] = true;           //否则, 将t加入集合S

        /*   更新集合V-S中与t邻接的顶点到u的距离,扩展当前最短路径树  */
    	for(int v = 0; v < G->nodenums; v++){
    	    if(!flag[v] && G->edge[t][v] != INF){
    		//不在集合S中 且 有边
                if(dist[v] > dist[t] + G->edge[t][v]){
                    //源点u可以借助t到达v的距离更短
                    dist[v] = dist[t] + G->edge[t][v];
                    pre[v] = t;
                }
    	    }
    	}
    }
}

---

还原具体路径代码

我使用了 C++ 自带的 栈 stack，来实现最短路径具体路径的还原。因为记录的是每个顶点的前驱，所以恰好可以利用 栈 stack 的先进后出的性质。

//还原源点u到各点具体路径
void ShowShortParth(Graph G, int u){
    for(int v = 0; v < G.nodenums; v++){
	if(dist[v] == INF || dist[v] == 0)
	    continue;
	cout<<"\n点"<<G.apex[u]<<" 到 点"<<G.apex[v]<<" 的最短路径距离为: "<<dist[v]<<endl;
	cout<<"点"<<G.apex[v]<<"的前驱顶点为: 点"<<G.apex[pre[v]]<<endl;
	cout<<"具体路径为: "<<endl;

	int t = pre[v];           //终点的前驱下标
	//用栈存储终点前驱们 一直到 源点
	stack<int> st;
	while(t != u){
	    st.push(t);
	    t = pre[st.top()];
	}

    	cout<<G.apex[u];          		//源点
	while(!st.empty()){
	    t = st.top();
	    cout<<" --> "<<G.apex[t];   //中间点
	    st.pop();
        }
	cout<<" --> "<<G.apex[v]<<endl; //终点
	cout<<"———————————————————"<<endl;
    }
}

---

完整程序(含图的邻接矩阵)

#include<iostream>
#include<cstdio>
#include<stack>
using namespace std;
const int MAX = 100;
const int INF = 1e7;

typedef char ApexType;			//顶点名称数据类型
typedef int EdgeType;			//边权数据类型

typedef struct {

	ApexType apex[MAX];			//顶点表
	EdgeType edge[MAX][MAX];	//矩阵图
	int nodenums, edgenums;		//顶点个数，边个数

}Graph;

//创建邻接矩阵
void CreateGraph(Graph *G){
    int i, j, k;
    int w;
    cout<<"输入顶点个数和边的条数: ";
    cin>>G->nodenums>>G->edgenums;
    //输入顶点信息
    for(i = 0; i < G->nodenums; i++){
	cout<<"输入第 "<<i + 1<<" 个顶点的名称: ";
	cin>>G->apex[i];
    }
    //初始化各顶点之间的边为无穷大
    for(i = 0; i < G->nodenums; i++)
	for(j = 0; j < G->nodenums; j++)
	    G->edge[i][j] = INF;
    //录入有向边的信息
    for(k = 0; k < G->edgenums; k++){
	EdgeType w;
	cout<<"输入<vi, vj>的对应点下标及权值: ";
	cin>>i>>j>>w;

        G->edge[i][j] = w;
    }
}

//打印图的邻接矩阵
void ShowGraphInMatrix(Graph *G){
    cout<<"   ";
    for(int i = 0; i < G->nodenums; i++)
	printf("%-4c",G->apex[i]);
    cout<<endl;

    for(int i = 0; i < G->nodenums; i++){
	printf("%-3c", G->apex[i]);
	for(int j = 0; j < G->nodenums; j++){
	    if(G->edge[i][j] == INF)
		cout<<"∞  ";
	    else
	        printf("%-4d", G->edge[i][j]);
	}
	cout<<endl;
    }
}

//距离记录数组 , 前驱数组
int dist[MAX], pre[MAX];
//集合S标记数组。如果flag[i]=true,说明该顶点i已经加入到集合S(最短路径集合);否则i属于集合V-S
bool flag[MAX];            

void Dijkstra(Graph *G, int u){
    for(int v = 0; v < G->nodenums; v++){
	dist[v] = G->edge[u][v];  //初始化源点u到各邻接点v的距离
	flag[v] = false;
	if(dist[v] != INF)
	    pre[v] = u;           //若有邻接边,顶点v有前驱顶点u
	else
	    pre[v] = -1;          //若没有,先初始化为-1
    }
    flag[u] = true;               //初始化集合S,只有一个元素: 源点u
    dist[u] = 0;                  //初始化源点u到自己的最短路径为0

    /*   在集合V-S中寻找距离源点u最近的顶点t,使当前最短路径树最优  */
    for(int i = 0; i < G->nodenums; i++){
    	int tmp = INF, t = u;
    	for(int v = 0; v < G->nodenums; v++){
    	    if(!flag[v] && dist[v] < tmp){
    		//不在集合S中 并且 更小距离
    		t = v;            //记录在V-S中距离源点u最近的顶点v
    		tmp = dist[v];
    	    }
    	}

    	if(t == u)
    	    return;               //未找到直接终止
    	flag[t] = true;           //否则, 将t加入集合S

        /*   更新集合V-S中与t邻接的顶点到u的距离,扩展当前最短路径树  */
    	for(int v = 0; v < G->nodenums; v++){
    	    if(!flag[v] && G->edge[t][v] != INF){
    		//不在集合S中 且 有边
                if(dist[v] > dist[t] + G->edge[t][v]){
                    //源点u可以借助t到达v的距离更短
                    dist[v] = dist[t] + G->edge[t][v];
                    pre[v] = t;
                }
    	    }
    	}
    }
}

//还原源点u到各点具体路径
void ShowShortParth(Graph G, int u){
    for(int v = 0; v < G.nodenums; v++){
	if(dist[v] == INF || dist[v] == 0)
	    continue;
	cout<<"\n点"<<G.apex[u]<<" 到 点"<<G.apex[v]<<" 的最短路径距离为: "<<dist[v]<<endl;
	cout<<"点"<<G.apex[v]<<"的前驱顶点为: 点"<<G.apex[pre[v]]<<endl;
	cout<<"具体路径为: "<<endl;

	int t = pre[v];           //终点的前驱下标
	//用栈存储终点前驱们 一直到 源点
	stack<int> st;
	while(t != u){
	    st.push(t);
	    t = pre[st.top()];
	}

    	cout<<G.apex[u];          		//源点
	while(!st.empty()){
	    t = st.top();
	    cout<<" --> "<<G.apex[t];   //中间点
	    st.pop();
        }
	cout<<" --> "<<G.apex[v]<<endl; //终点
	cout<<"———————————————————"<<endl;
    }
}

main(){
    Graph G;
    CreateGraph(&G);
    ShowGraphInMatrix(&G);

    int u;
    cout << "\n输入出发的源点下标: ";
    cin>>u;

    Dijkstra(&G, u);

    cout<<"\n源点到所有点的单源最短路径距离:"<<endl;
    ShowShortParth(G, v);
}

---

程序运行图

图的输入和邻接矩阵打印

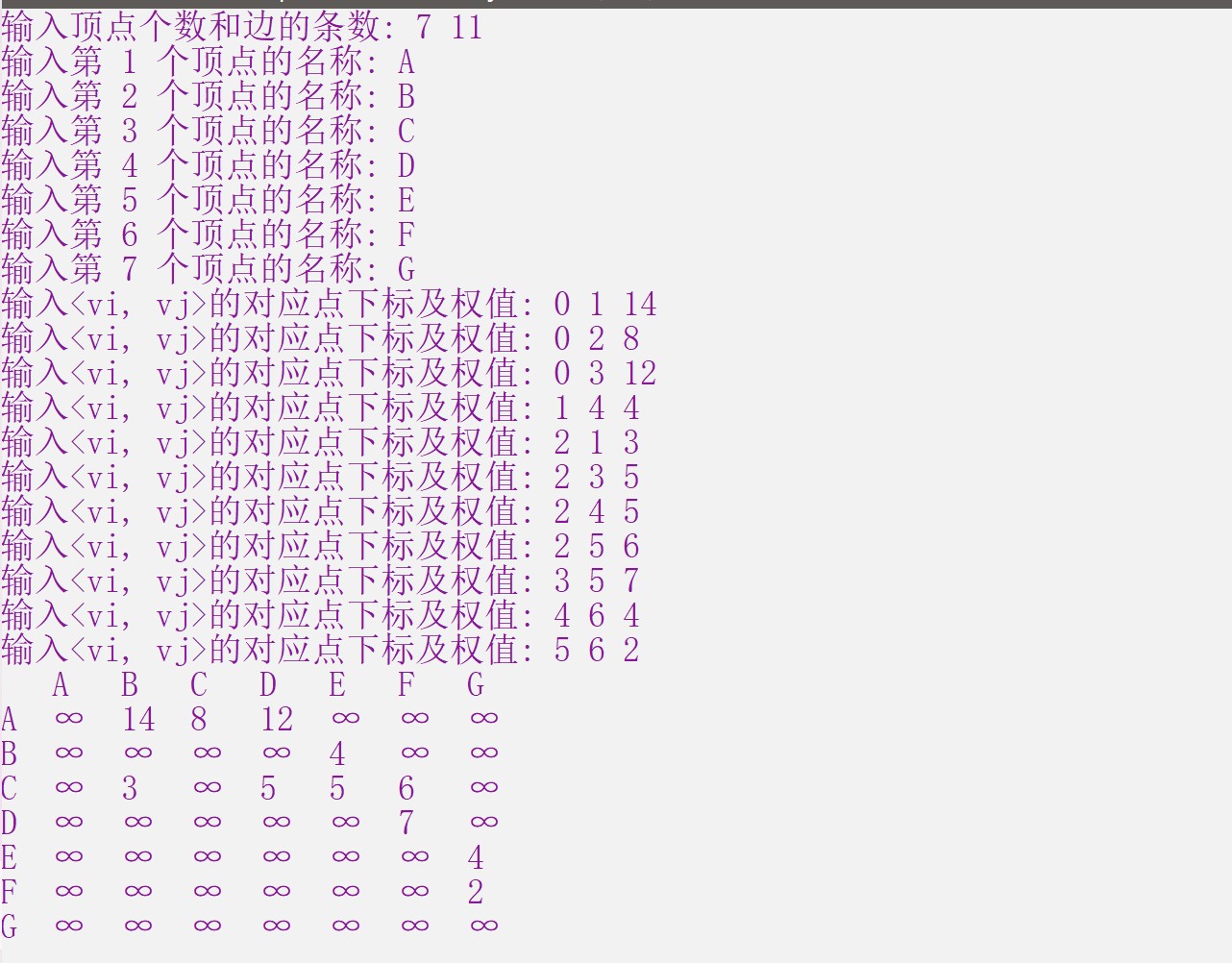
单源最短路径及具体路径