运筹学之"连通图"和"最小枝杈树"和"最短路线问题"
一.连通图
必须每个点都有关系
- 图1 不算连通图
- 图2含有圈v1,v2,v5,可优化
- 图3就是所需的连通图
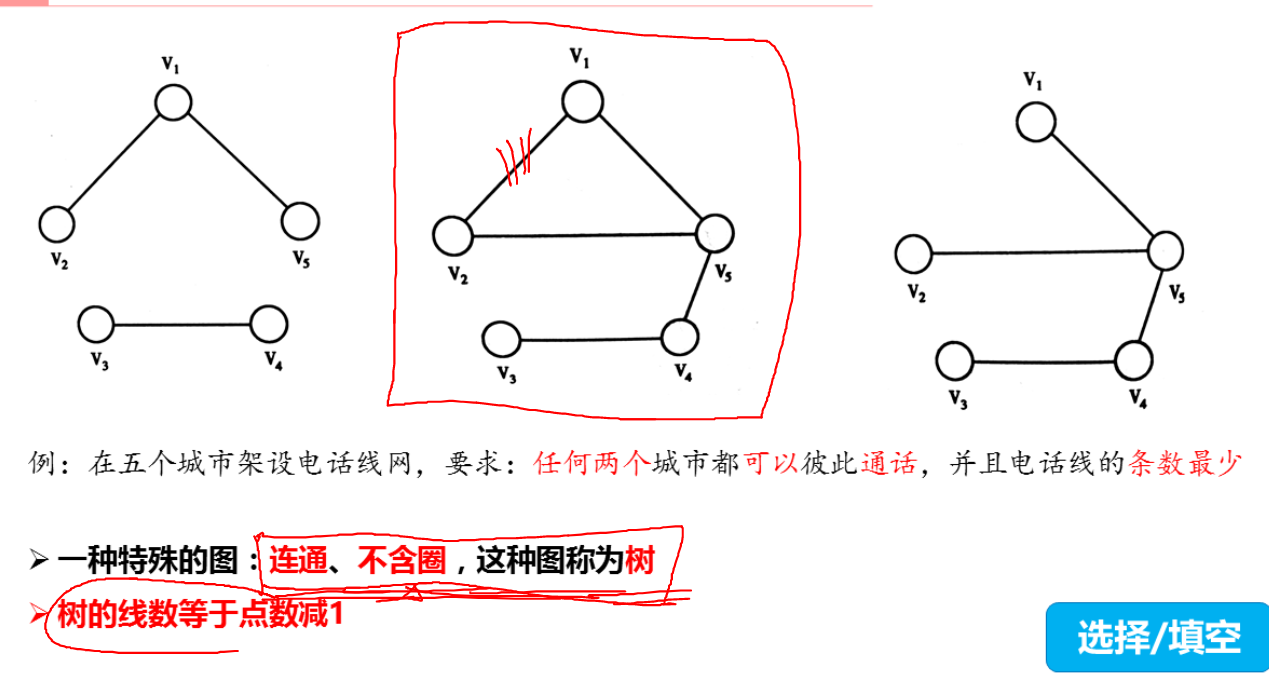
注意:图>连通图>树
二.最小枝杈树
获取是所有节点的最小值,只要是连通图就好,所有长度最短的路线
可以采用是"普赖姆法"用于大型网络
可以采用是"克鲁斯咯尔法"用于小的手工计算机网络,在大型中的效率就比较低了
案例1
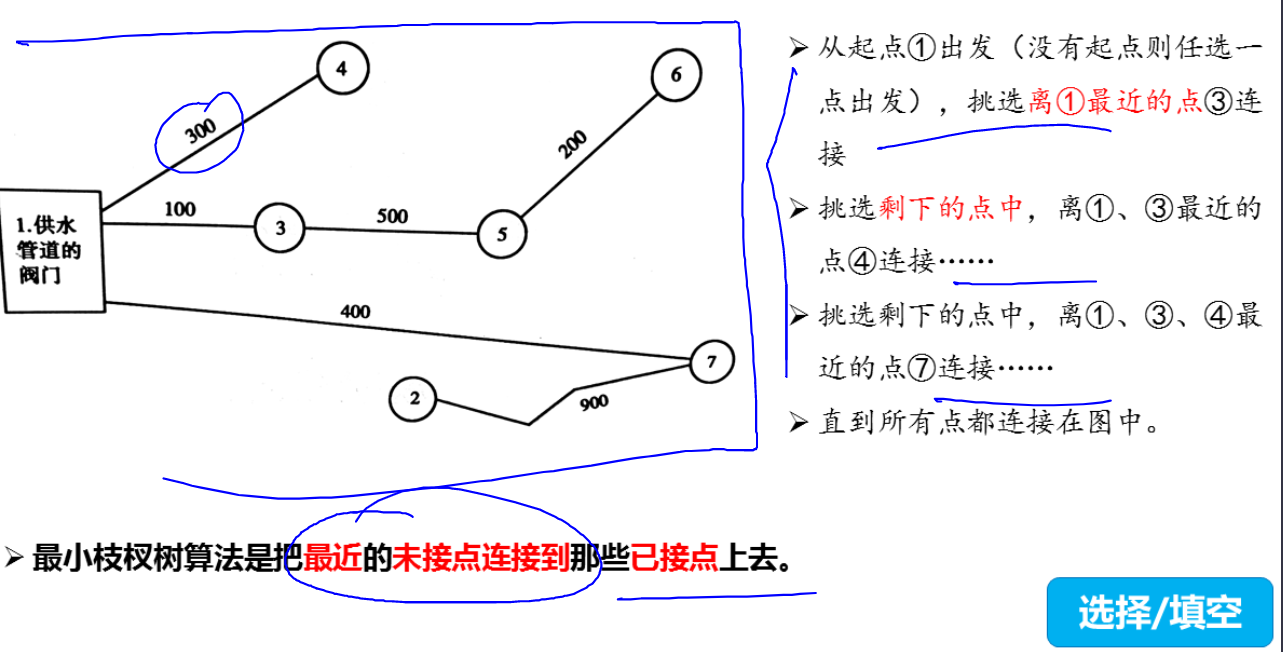
案例2
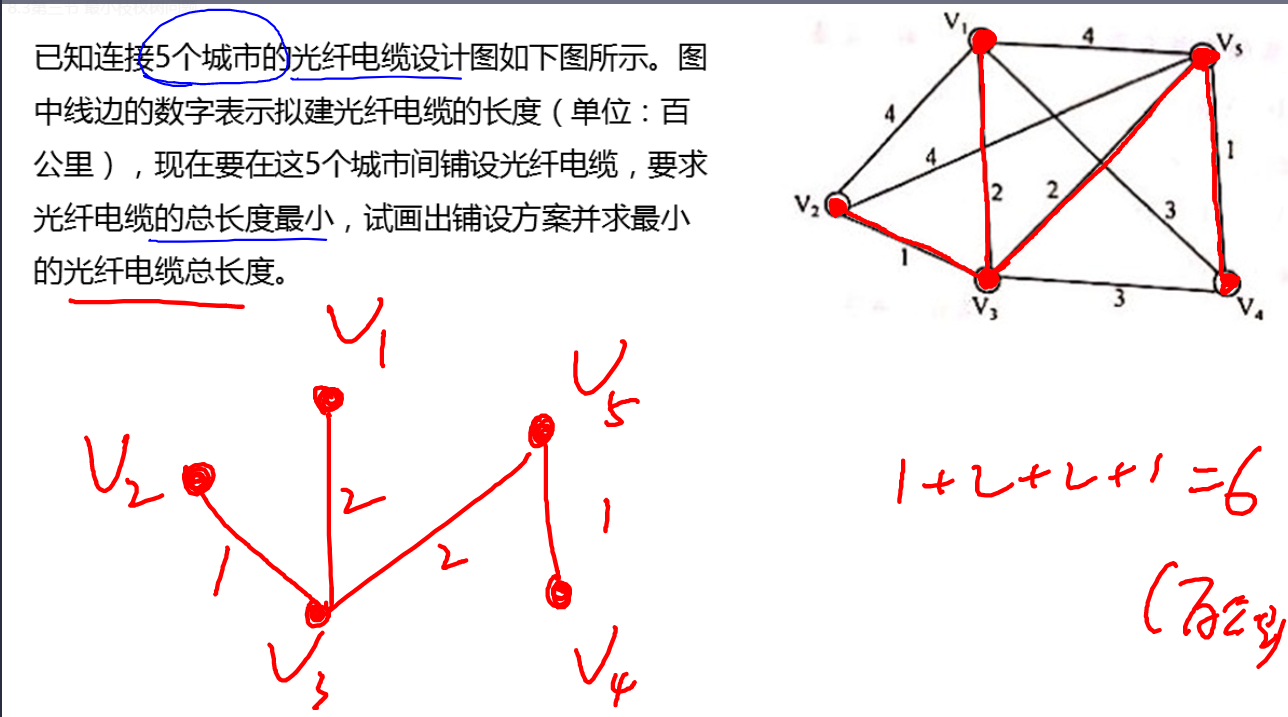
三.最短路线问题
从头到位最小值,最优路径
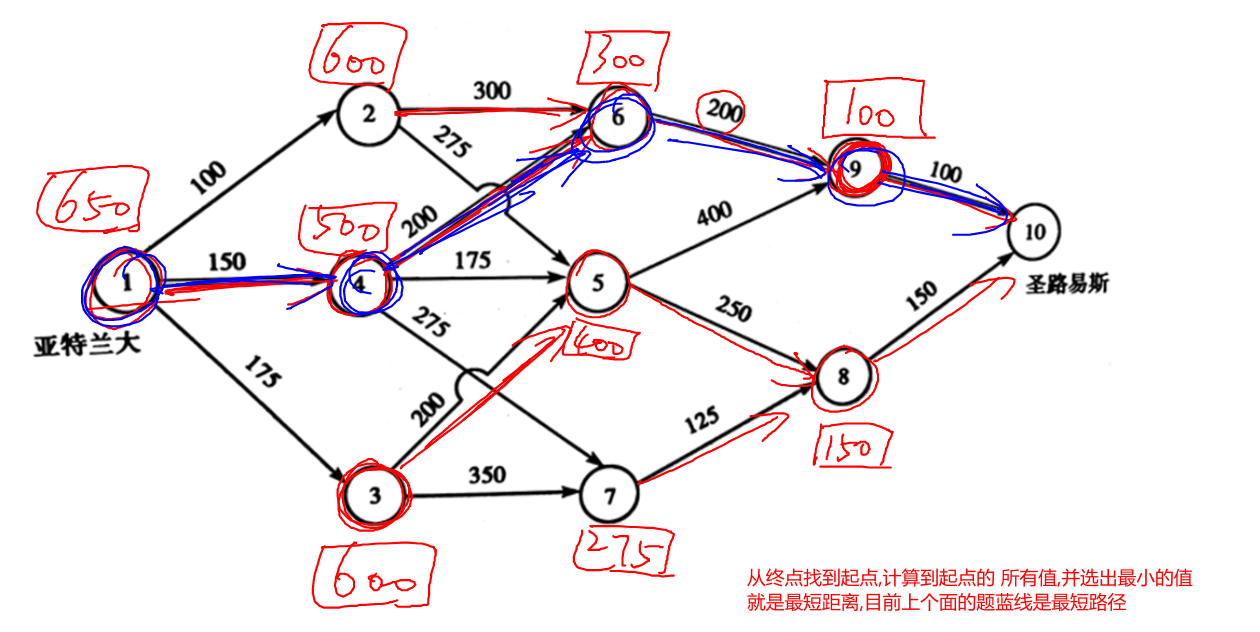
案例
可以试下去其他路径,不会比6小了
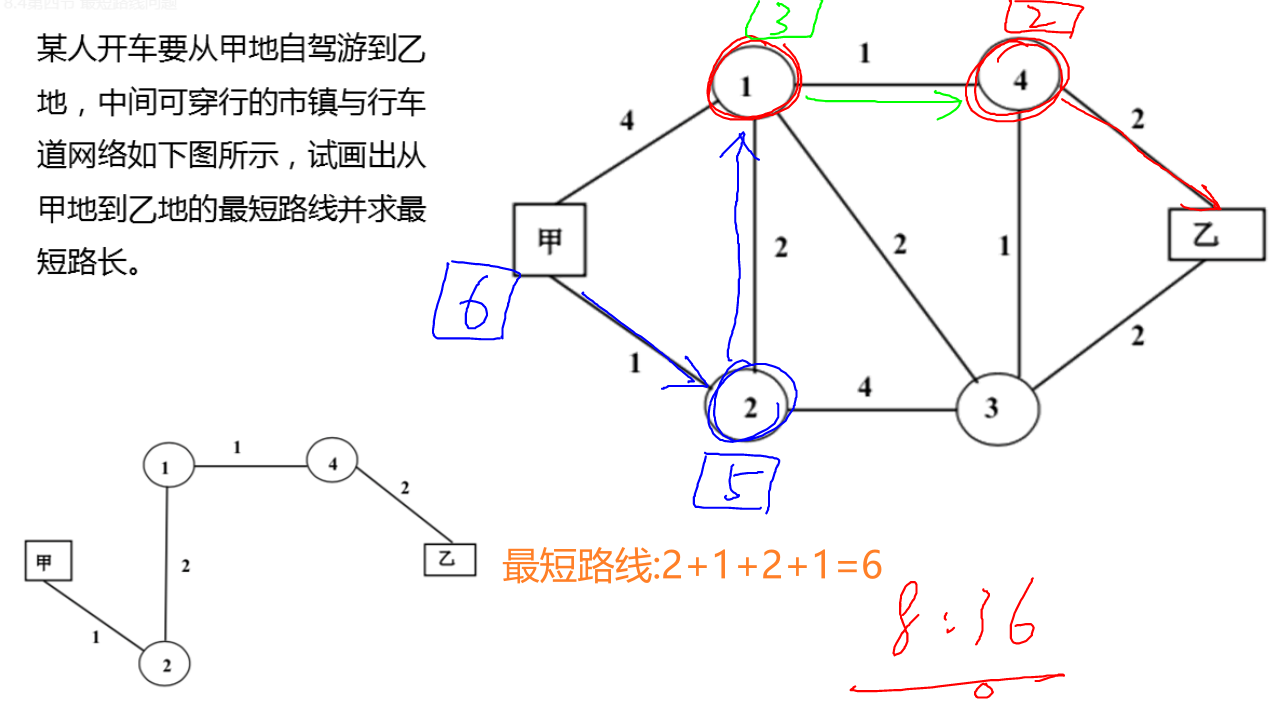
四.最大流量问题
至少通过流量
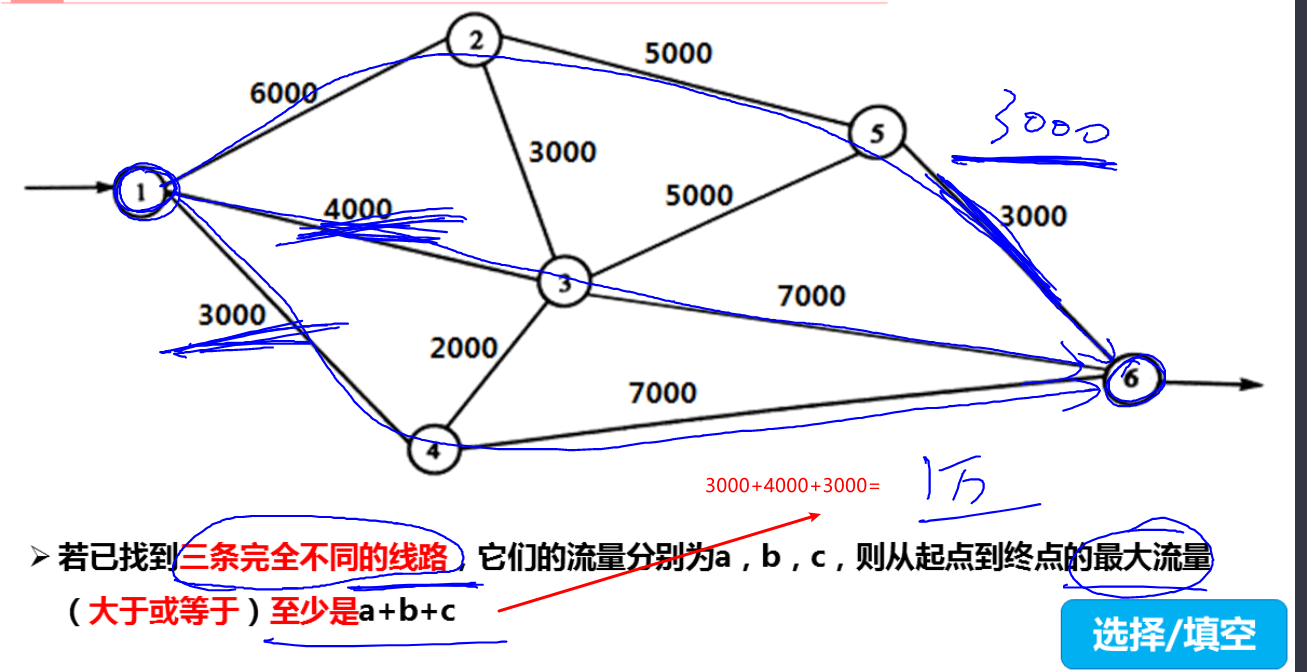
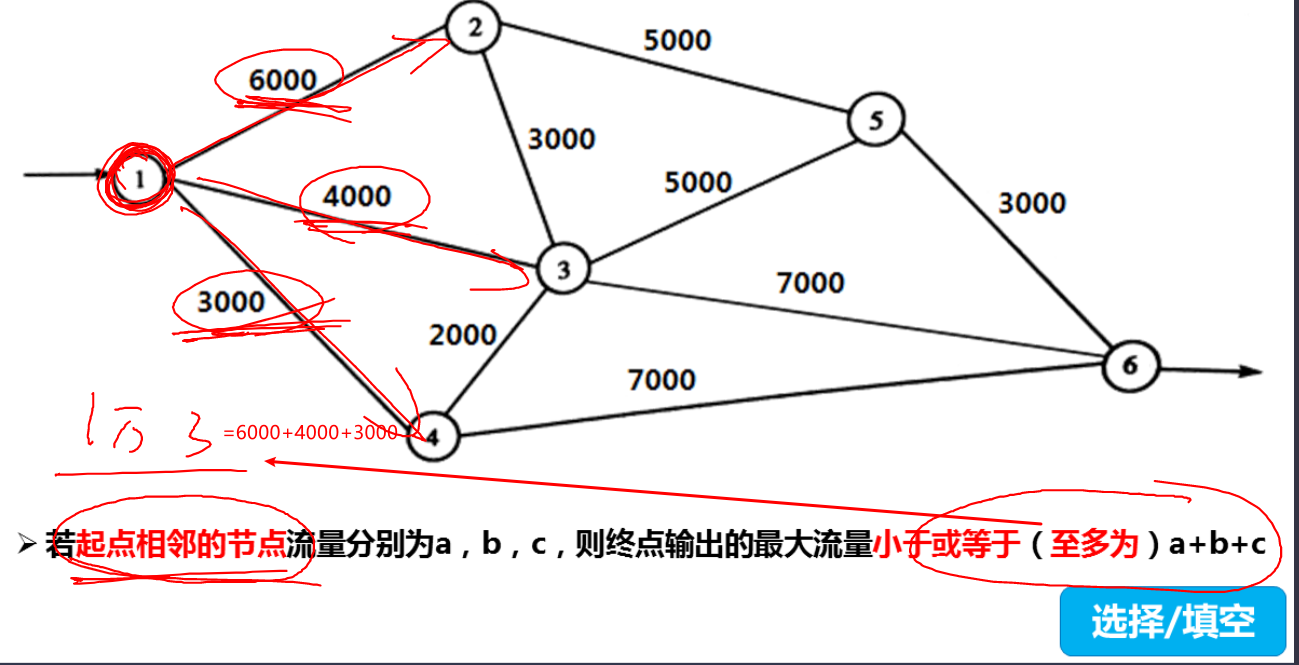
至多通过流量
运筹学之"连通图"和"最小枝杈树"和"最短路线问题"的更多相关文章
- [Swift]LeetCode310. 最小高度树 | Minimum Height Trees
For an undirected graph with tree characteristics, we can choose any node as the root. The result gr ...
- BZOJ4519[Cqoi2016]不同的最小割——最小割树+map
题目描述 学过图论的同学都知道最小割的概念:对于一个图,某个对图中结点的划分将图中所有结点分成 两个部分,如果结点s,t不在同一个部分中,则称这个划分是关于s,t的割.对于带权图来说,将 所有顶点处在 ...
- LoibreOJ 2042. 「CQOI2016」不同的最小割 最小割树 Gomory-Hu tree
2042. 「CQOI2016」不同的最小割 内存限制:256 MiB时间限制:1000 ms标准输入输出 题目类型:传统评测方式:文本比较 上传者: 匿名 提交提交记录统计讨论测试数据 题目描述 ...
- 不同的最小割(cqoi2016,bzoj4519)(最小割树)
学过图论的同学都知道最小割的概念:对于一个图,某个对图中结点的划分将图中所有结点分成 两个部分,如果结点\(s,t\)不在同一个部分中,则称这个划分是关于\(s,t\)的割.对于带权图来说,将 所有顶 ...
- [模板]最小割树(Gomory-Hu Tree)(luogu4897)
给定一个\(n\)个点\(m\)条边的无向连通图,多次询问两点之间的最小割 两点间的最小割是这样定义的:原图的每条边有一个割断它的代价,你需要用最小的代价使得这两个点不连通 Input 第一行两个数\ ...
- Leetcode 310.最小高度树
最小高度树 对于一个具有树特征的无向图,我们可选择任何一个节点作为根.图因此可以成为树,在所有可能的树中,具有最小高度的树被称为最小高度树.给出这样的一个图,写出一个函数找到所有的最小高度树并返回他们 ...
- 【模板】最小割树（Gomory-Hu Tree）
传送门 Description 给定一个\(n\)个点\(m\)条边的无向连通图,多次询问两点之间的最小割 两点间的最小割是这样定义的:原图的每条边有一个割断它的代价,你需要用最小的代价使得这两个点不 ...
- leetcode.310最小高度树
对于一个具有树特征的无向图,我们可选择任何一个节点作为根.图因此可以成为树,在所有可能的树中,具有最小高度的树被称为最小高度树.给出这样的一个图,写出一个函数找到所有的最小高度树并返回他们的根节点. ...
- Java实现 LeetCode 310 最小高度树
310. 最小高度树 对于一个具有树特征的无向图,我们可选择任何一个节点作为根.图因此可以成为树,在所有可能的树中,具有最小高度的树被称为最小高度树.给出这样的一个图,写出一个函数找到所有的最小高度树 ...
随机推荐
- 【C# IO 操作 】内存包装类 Memory <T>和 Span<T> 相关类型
简介 .NET 包含多个相互关联的类型,它们表示任意内存的连续的强类型区域. 这些方法包括: System.Span<T> 用于访问连续的内存区域 得到该类型的实例: 1个T类型的数组 1 ...
- MapReduce中一次reduce方法的调用中key的值不断变化
简单一句话总结就是:ReduceContextImpl类的RawKeyValueIterator input迭代器对象里面存储中着key-value对的元素, 以及一个只存储value的迭代器,然后每 ...
- 压力测试工具——jmeter
Jmeter:这是一个绿色的工具,但是它需要依赖与jdk 8的环境,所以在安装的时候需要安装jdk8. 下载地址: 链接:https://pan.baidu.com/s/1pGj1hAqJBBoSHf ...
- 关于malloc源码中的bin_at宏定义的个人见解
0x01:简介 在堆中的内存申请和释放中,为了减少使用系统调用函数对内存操作,malloc_state(分配区)结构中使用了fastbinsY数组和bins数组.当chunk被free后,bins链会 ...
- LGP5591题解
题意很明确,不说了. 前置芝士:单位根反演 也就是: \[[n|a]=\frac 1 n \sum_{i=0}^{n-1}w_n^{ai} \] 看到题目给的柿子: \[\sum_{i=0}^n\bi ...
- xilinx SDK在线仿真_烧写 提示失败
1.找到工程目录下的Binaries->xxx.elf-[arm/le] . 2.右击该elf,选择Debug As->Debug Configurations... 进入设置界面. 3. ...
- IC设计基础
一 前言 这一周连续两场线下面试,紧接着又是微信视频面试,从连续三天的面试中,收获颇丰! 存在的问题: 一是对项目细节模糊: 二是IC基础知识薄弱: 具体表现是,在面试过程中,如被问到DDR3和千兆以 ...
- 动态规划优化算法——wqs二分 and 折线优化
坑先扔着,督促自己以后来补!!!
- 统计分析— 1.SPSS数据编辑窗口 输出窗口 语法窗口
第一课-SPSS窗口 一 数据编辑窗口(Data Editor) 二 输出窗口(Output Viewer ) 三 语法窗口(Syntax Editor):针对中高级用户,有些操作可以通过输入代码的方 ...
- 什么叫 CC 攻击？什么叫 DDOS 攻击？
CC 攻击,主要是用来攻击页面的,模拟多个用户不停的对你的页面进行访问,从而使你的系统资源消耗殆尽.DDOS 攻击,中文名叫分布式拒绝服务攻击,指借助服务器技术将多个计算机联合起来作为攻击平台,来对一 ...