2016 Multi-University Training Contest 6

5/12

2016 Multi-University Training Contest 6

官方题解

打表找规律/推公式 A A Boring Question（BH）

题意：

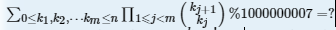　　，意思就是在[0,n]里选择m个数字的相邻数字二项式组合的积的总和。

思路：

想了好久，不会，但是这题有300多人过，怀疑人生。。。

打了个表：

n=0, m=2, ans=1
n=1, m=2, ans=3
n=2, m=2, ans=7
n=3, m=2, ans=15
n=4, m=2, ans=31
n=5, m=2, ans=63
n=6, m=2, ans=127
n=7, m=2, ans=900198674
n=8, m=2, ans=1590575918
n=0, m=3, ans=1
n=1, m=3, ans=4
n=2, m=3, ans=13
n=3, m=3, ans=40
n=4, m=3, ans=121
n=5, m=3, ans=364
n=6, m=3, ans=1093
n=7, m=3, ans=-457914394
n=8, m=3, ans=-624508303
n=0, m=4, ans=1
n=1, m=4, ans=5
n=2, m=4, ans=21
n=3, m=4, ans=85
n=4, m=4, ans=341
n=5, m=4, ans=1365
n=6, m=4, ans=5461
n=7, m=4, ans=-914025821
n=8, m=4, ans=-1903277640
n=0, m=5, ans=1
n=1, m=5, ans=6
n=2, m=5, ans=31
n=3, m=5, ans=156
n=4, m=5, ans=781
n=5, m=5, ans=3906
n=6, m=5, ans=19531
n=7, m=5, ans=-681221710
n=8, m=5, ans=1872878440
n=0, m=6, ans=1
n=1, m=6, ans=7
n=2, m=6, ans=43
n=3, m=6, ans=259
n=4, m=6, ans=1555
n=5, m=6, ans=9331
n=6, m=6, ans=55987
n=7, m=6, ans=-199384196
n=8, m=6, ans=638696943

按照m排序就能看出规律，想到比赛快结束的时候，最后没时间交题了，好气啊。

官方解答：

代码：

#include <bits/stdc++.h>

typedef unsigned long long ll;
const int N = 1e5 + 5;
const int MOD = 1000000007;
int fact[N];

void init_fact(int n) {
    fact[0] = 1;
    for (int i=1; i<=n; ++i) {
        fact[i] = (ll) fact[i-1] * i % MOD;
    }
}

int pow_mod(int x, int n, int MOD) {
    int ret = 1;
    for (; n; n>>=1) {
        if (n & 1) ret = (ll) ret * x % MOD;
        x = (ll) x * x % MOD;
    }
    return ret;
}

int Inv(int x) {
    return pow_mod (x, MOD - 2, MOD);
}

int n, m;
int tot;
int k[N], b[N];

int calc() {
    int ret = 0;
    int tmp = 1;
    for (int i=2; i<=m; ++i) {
        tmp = (ll) tmp * fact[b[i]] % MOD;
    }
    ret = (ll) fact[k[m]] * Inv (fact[k[1]]) % MOD * Inv (tmp) % MOD;
    return ret;
}

void DFS(int cur, int len, int &ans) {
    if (len == m + 1) {
        ans += calc ();
        return ;
    }
    for (int i=0; i<=n; ++i) {
        k[len] = i; b[len] = k[len] - k[len-1];
        DFS (i, len+1, ans);
    }
}

int brute(int n, int m) {
    int ret = 0;
    for (int i=0; i<=n; ++i) {
        k[1] = i;
        DFS (i, 2, ret);
    }
    return ret;
}

int solve() {
    if (n == 0) return 1;
    return (1 + (ll) m * (pow_mod (m, n, MOD) - 1 + MOD) % MOD * Inv (m - 1)) % MOD;
}

int main() {
    int T;
    scanf ("%d", &T);
    while (T--) {
        scanf ("%d%d", &n, &m);
        //printf ("%d\n", brute (n, m));
        printf ("%d\n", solve ());
    }
    return 0;
}

容斥原理+Lucas定理 B A Simple Chess（BH）

题意：

　　n*m的格子，有r个障碍物，从(1,1)出发不走到障碍物到达(n,m)的方案数。（走法是(x1,y1)->(x1+2,y1+1) or (x1+1,y1+2)）

思路：

　　记第一种走法的次数为b次，第二种走法的次数为c次，那么n=1+2c+b，m=1+2b+c。如果不考虑障碍物的话，答案是。那么如果会走到第i个障碍物，那么减去的是从(1,1)到第i个障碍物的位置的方案数（不走到其他的障碍物）乘以从第i个障碍物出发到(n,m)的方案数。注意(n,m)是障碍物的话，方案数直接为0。有了想法后，用代码实现，检验正确性，获得AC，瞬间的快感，这就是ACM的魅力吧。

代码：

#include <bits/stdc++.h>

typedef long long ll;
const int N = 100 + 5;
const int MOD = 110119;

ll pow_mod(ll x, int n) {
    ll ret = 1;
    for (; n; n>>=1) {
        if (n & 1) ret = ret * x % MOD;
        x = x * x % MOD;
    }
    return ret;
}

ll Inv(ll x) {
    return pow_mod (x, MOD - 2);
}

ll fact[MOD];

struct Point {
    ll x, y;
    bool operator < (const Point &rhs) const {
        ll ldis = (x - 1) + (y - 1);
        ll rdis = (rhs.x - 1) + (rhs.y - 1);
        return ldis < rdis;
    }
}p[N];
ll res[N];
ll n, m;
int r;

void init_fact(int n) {
    fact[0] = 1;
    for (int i=1; i<n; ++i) {
        fact[i] = fact[i-1] * i % MOD;
    }
}

ll Lucas(ll n, ll k, int p) {
    ll ret = 1;
    while (n && k) {
        ll nn = n % p, kk = k % p;
        if (nn < kk) return 0;
        ret = ret * fact[nn] % p * Inv (fact[kk] * fact[nn-kk] % p) % p;
        n /= p; k /= p;
    }
    return ret;
}

bool judge_b(ll n, ll m) {
    return (-n + 2 * m - 1) % 3 == 0 && (-n + 2 * m - 1) >= 0;
}

bool judge_c(ll n, ll m) {
    return (2 * n - m - 1) % 3 == 0 && (2 * n - m - 1) >= 0;
}

ll get_b(ll n, ll m) {
    return (-n + 2 * m -1) / 3;
}

ll get_c(ll n, ll m) {
    return (2 * n - m - 1) / 3;
}

ll solve() {
    //if (r > 0 && p[r-1].x == n && p[r-1].y == m) return 0;
    if (!judge_b (n, m)) return 0;
    if (!judge_c (n, m)) return 0;
    ll b = get_b (n, m);
    ll c = get_c (n, m);
    ll ret = Lucas (b + c, c, MOD);

    std::sort (p, p+r);
    memset (res, -1, sizeof (res));
    for (int i=0; i<r; ++i) {
        if (!judge_b (p[i].x, p[i].y)) continue;
        if (!judge_c (p[i].x, p[i].y)) continue;
        if (!judge_b (n-p[i].x+1, m-p[i].y+1)) continue;
        if (!judge_c (n-p[i].x+1, m-p[i].y+1)) continue;
        ll ib = get_b (p[i].x, p[i].y);
        ll ic = get_c (p[i].x, p[i].y);
        res[i] = Lucas (ib+ic, ib, MOD);

        for (int j=0; j<i; ++j) {
            if (res[j] == -1) continue;
            if (p[i].x < p[j].x || p[i].y < p[j].y) continue;
            ll nn = p[i].x - p[j].x + 1;
            ll mm = p[i].y - p[j].y + 1;
            if (!judge_b (nn, mm))  continue;
            if (!judge_c (nn, mm)) continue;
            ll jb = get_b (nn, mm);
            ll jc = get_c (nn, mm);
            ll tmp = res[j] * Lucas (jb+jc, jb, MOD) % MOD;
            res[i] = (res[i] - tmp + MOD) % MOD;
        }
        ll nb = get_b (n-p[i].x+1, m-p[i].y+1);
        ll nc = get_c (n-p[i].x+1, m-p[i].y+1);
        ret = (ret - res[i] * Lucas (nb+nc, nb, MOD) % MOD + MOD) % MOD;
    }
    return ret;
}

int main() {
    init_fact (MOD);
    int cas = 0;
    while (scanf ("%I64d%I64d%d", &n, &m, &r) == 3) {
        bool flag = true;
        for (int i=0; i<r; ++i) {
            scanf ("%I64d%I64d", &p[i].x, &p[i].y);
            if (p[i].x == n && p[i].y == m) flag = false;
        }
        if (!flag) {
            printf ("Case #%d: %I64d\n", ++cas, 0LL);
            continue;
        }
        printf ("Case #%d: %I64d\n", ++cas, solve ());
    }
    return 0;
}

博弈+打表找规律 C A Simple Nim（BH）

题意：

　　除了经典的Nim走法，还多了可以把一堆分成三小堆的走法。

思路：

　　多了一种操作没关系，根据SG定理，只要求出x的所有后继状态的SG函数，SG(x)=mex(S)，分成三小堆的状态的SG值看成三个子游戏的Nim和。至于这题的做法，打表找规律即可。

代码：

#include <bits/stdc++.h>

int sg[105];

int SG(int n) {
    if (n == 0) return sg[n] = 0;
    if (sg[n] != -1) return sg[n];
    if (n < 3) return sg[n] = n;
    bool vis[1000];
    memset (vis, false, sizeof (vis));
    for (int i=1; i<=n; ++i) {
        for (int j=i; i+j<n; ++j) {
            int k = n - i - j;
            //if (k < i || k < j) continue;
            vis[SG (i) ^ SG (j) ^ SG (k)] = true;
        }
    }
    for (int i=0; i<n; ++i) vis[SG (i)] = true;
    int &ret = sg[n] = 0;
    while (vis[ret]) ret++;
    return ret;
}

void f() {
    memset (sg, -1, sizeof (sg));
    for (int i=0; i<=100; ++i) {
        printf ("sg[%d]=%d\n", i, SG (i));
    }
}

int main() {
    //f ();
    int T;
    scanf ("%d", &T);
    while (T--) {
        int n;
        scanf ("%d", &n);
        long long ans = 0;
        for (int i=0; i<n; ++i) {
            long long x;
            scanf ("%I64d", &x);
            long long sg = x;
            if (x % 8 == 0) sg--;
            if (x % 8 == 7) sg++;
            ans ^= sg;
        }
        puts (ans ? "First player wins." : "Second player wins.");
    }
    return 0;
}

01背包 H To My Girlfriend（BH）

题意：

　　，意思是有a[i]，a[j]，没有a[k]，a[l]，和为m时的组合数。

思路：

　　想到简单的背包DP，dp[i][j][s1][s2]表示考虑前i个，和为j，且必选了s1个且必不选s2个的方案数。时间复杂度为。

#include <bits/stdc++.h>

const int N = 1e3 + 5;
const int MOD = 1e9 +7;
int dp[N][N][3][3];
int a[N];
int n, s;

void add_mod(int &a, int b) {
    a += b;
    if (a >= MOD) a -= MOD;
}

int solve() {
    memset (dp, 0, sizeof (dp));
    dp[0][0][0][0] = 1;
    for (int i=1; i<=n; ++i) {
        for (int j=0; j<=s; ++j) {
            for (int s1=0; s1<=2; ++s1) {
                for (int s2=0; s2<=2; ++s2) {
                    add_mod (dp[i][j][s1][s2], dp[i-1][j][s1][s2]);  //不选
                    if (j >= a[i]) add_mod (dp[i][j][s1][s2], dp[i-1][j-a[i]][s1][s2]);  //选
                    if (j >= a[i] && s1) add_mod (dp[i][j][s1][s2], dp[i-1][j-a[i]][s1-1][s2]);  //必选
                    if (s2) add_mod (dp[i][j][s1][s2], dp[i-1][j][s1][s2-1]);  //必不选
                }
            }
        }
    }
    int ret = 0;
    for (int i=1; i<=s; ++i) {
        add_mod (ret, dp[n][i][2][2]);
    }
    return (long long) ret * 4 % MOD;
}

int main() {
    int T;
    scanf ("%d", &T);
    while (T--) {
        scanf ("%d%d", &n, &s);
        for (int i=1; i<=n; ++i) scanf ("%d", a+i);
        printf ("%d\n", solve ());
    }
    return 0;
}

贪心 J Windows 10（BH）

题意：

　　调音量从p到q，调低的操作，连续的情况下，1，2，4。。。停顿和上升操作都会打断连续，重新从1开始，问最少几次操作。

思路：

　　直观的想法就是拼命的往下降，最后微调（上升或者停顿再下降），考虑到”停顿+一格音量“可以与”上升一格“互换，那么在下降后再上升时考虑能否用停顿替代部分上升，所以要记录停顿的次数，DFS写很好。

#include <bits/stdc++.h>

typedef long long ll;

ll DFS(ll p, ll q, ll step, ll stop) {
    if (p == q) return step;
    int x = 0;
    while (p - (1<<x) + 1 > q) x++;
    if (p - (1<<x) + 1 == q) return step + x;
    ll up = q - std::max (0LL, (p - (1<<x) + 1));
    ll better = x + std::max (0LL, up - stop);
    return std::min (better + step, DFS (p-(1<<(x-1))+1, q, step+x, stop+1));
}

int main() {
    int T;
    scanf ("%d", &T);
    while (T--) {
        ll p, q;
        scanf ("%I64d%I64d", &p, &q);
        if (q >= p) {
            printf ("%I64d\n", q - p);
        } else {
            printf ("%I64d\n", DFS (p, q, 0, 0));
        }
    }
    return 0;
}