【小白学游戏常用算法】二、A*启发式搜索算法

　　在上一篇博客中，我们一起学习了随机迷宫算法，在本篇博客中，我们将一起了解一下寻路算法中常用的A*算法。

　　通常情况下，迷宫寻路算法可以使用深度优先或者广度优先算法，但是由于效率的原因，不会直接使用这些算法，在路径搜索算法中最常见的就是A*寻路算法。使用A*算法的魅力之处在于它不仅能找到地图中从A到B的一条路径，还能保证找到的是一条最短路径，它是一种常见的启发式搜索算法，类似于Dijkstra算法一样的最短路径查找算法，很多游戏应用中的路径搜索基本都是采用这种算法或者是A*算法的变种。

　　下面我们来了解一下A*算法相关的理论知识：

　　

　　如图，我们需要在迷宫中找到A点到B点的一条最短的可以通过的路径，A和B直接被一面墙堵住了。在上一篇博客中我们说到了，地图是有二维数组组成的，墙表示不能通过的地方，用1表示，A*算法所要做的就是从A找到一条最短的通向B的路径。当然，不能从墙上飞过去，也不能瞬移到B。只能每次移动一个格子，一步一步地移动到B目标位置。问题在于，每次移动一格的时候，有上下左右四个方向，这里我们限制物体斜向移动，如何选择下一个移动方向呢？按照我们的想法，不就是找一条离目标最近的路吗？那我们可以在这四个方向中，找一个最接近目标点的位置，当然，还要考虑障碍因素，基于这个思想，A*算法采用了以下的搜索步骤来实现：

　　1.首先把起始位置点加入到一个称为“open List”的列表，在寻路的过程中，目前，我们可以认为open List这个列表会存放许多待测试的点，这些点是通往目标点的关键，以后会逐渐往里面添加更多的测试点，同时，为了效率考虑，通常这个列表是个已经排序的列表。

　　2.如果open List列表不为空，则重复以下工作：

　　（1）找出open List中通往目标点代价最小的点作为当前点；

　　（2）把当前点放入一个称为close List的列表；

　　（3）对当前点周围的4个点每个进行处理（这里是限制了斜向的移动），如果该点是可以通过并且该点不在close List列表中，则处理如下；

　　（4）如果该点正好是目标点，则把当前点作为该点的父节点，并退出循环，设置已经找到路径标记；

　　（5）如果该点也不在open List中，则计算该节点到目标节点的代价，把当前点作为该点的父节点，并把该节点添加到open List中；

　　（6）如果该点已经在open List中了，则比较该点和当前点通往目标点的代价，如果当前点的代价更小，则把当前点作为该点的父节点，同时，重新计算该点通往目标点的代价，并把open List重新排序；

　　3.完成以上循环后，如果已经找到路径，则从目标点开始，依次查找每个节点的父节点，直到找到开始点，这样就形成了一条路径。

　　以上，就是A*算法的全部步骤，按照这个步骤，就可以得到一条正确的路径。这里有一个关键的地方，就是如何计算每个点通往目标点的代价，之所以称为A*算法为启发式搜索，就是因为通过评估这个代价值来搜索最近的路径，对于任意一个点的代价值，在A*算法中通常使用下列的公式计算：

代价F=G+H

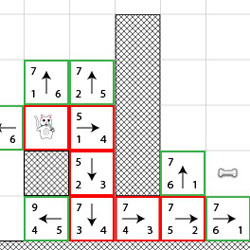
　　在这里，F表示通往目标点的代价，G表示从起始点移动到该点的距离，H则表示从该点到目标点的距离，比如图中，可以看到小狗的附近格子的代价值，其中左上角的数字代表F值，左下角的数字代表G值，右下角的数字代表H值。拿小狗上方的格子来举例，G=1，表示从小狗的位置到该点的距离为1个格子，H=6，表示从小狗到骨头的距离是6个格子，则F=G+H=7。在此处，距离的算法是采用曼哈顿距离，它计算从当前格子到目的格子之间水平和垂直的方格的数量总和，例如在平面上，坐标（x1,y1）的点和坐标（x2,y2）的点的曼哈顿距离为：

|x1-x2|+|y1-y2|

　　当然，距离的算法也可以采用其他的方法，实际在游戏中，这个移动的代价除了要考虑距离因素外，还要考虑当前格子的游戏属性。比如有的格子表示水路、草地、陆地，这些有可能影响人物移动的速度，实际计算的时候还要把这些考虑在内。

　　另一个需要注意的就是，在计算这个距离的时候是毋须考虑障碍因素的，因为在以上A*算法步骤中会剔除掉障碍。

　　这样，按照前面所说的A*算法的步骤，第一次循环open List的时候，把A点作为当前点，同时把A周围的四个点放入到open List中。第二次循环的时候把A右边的点作为当前点，该点的父节点就是A，这是处理当前点的时候，只需要把当前点的上下两个点放入open List中，因为左边的A已经在close List中，而右边的是墙，所以直接被忽略。

　　A*的算法具体代码如下：

 //地图工具
    var _MapUtil = win.MapUtil =
    {
       //定义点对象
       Point:function(x,y)
        {
            this.x = x;
            this.y = y;
            this.parent = null;
            this.f = 0;
            this.g = 0;
            this.h=0;
            //当前点状态，0：表示在openlist 1:表示closelist,-1表示还没处理
            this.state=-1;
            //flag表明该点是否可通过
            this.flag = 0;
        },
        //产生随机迷宫
        primMaze:function(r,c)
        {
          //初始化数组
          function init(r,c)
          {
             var a = new Array(2*r+1);
             //全部置1
             for(var i=0,len=a.length;i<len;i++)
             {
                var cols = 2*c+1;
                a[i]= new Array(cols);
                ArrayUtil.fillWith(a[i],1);
             }
             //中间格子为0
             for(var i=0;i<r;i++)
              for(var j=0;j<c;j++)
                 {
                    a[2*i+1][2*j+1] = 0;
                 }
             return a;
          }
          //处理数组，产生最终的数组
          function process(arr)
          {
            //acc存放已访问队列，noacc存放没有访问队列
            var acc = [],noacc = [];
            var r = arr.length>>1,c=arr[0].length>>1;
            var count = r*c;
            for(var i=0;i<count;i++){noacc[i]=0;}
            //定义空单元上下左右偏移
            var offs=[-c,c,-1,1],offR=[-1,1,0,0],offC=[0,0,-1,1];
            //随机从noacc取出一个位置
            var pos = MathUtil.randInt(count);
            noacc[pos]=1;
            acc.push(pos);
            while(acc.length<count)
            {
              var ls = -1,offPos = -1;
              offPos = -1;
              //找出pos位置在二维数组中的坐标
              var pr = pos/c|0,pc=pos%c,co=0,o=0;
              //随机取上下左右四个单元
              while(++co<5)
              {
                o = MathUtil.randInt(0,5);
                ls =offs[o]+pos;
                var tpr = pr+offR[o];
                var tpc = pc+offC[o];
                if(tpr>=0&&tpc>=0&&tpr<=r-1&&tpc<=c-1&&noacc[ls]==0){ offPos = o;break;}
              }
              if(offPos<0)
              {

                 pos = acc[MathUtil.randInt(acc.length)];
              }
              else
              {
                 pr = 2*pr+1;
                 pc = 2*pc+1;
                 //相邻空单元中间的位置置0
                 arr[pr+offR[offPos]][pc+offC[offPos]]=0;
                 pos = ls;
                 noacc[pos] = 1;
                 acc.push(pos);
              }
            }
          }
          var a = init(r,c);
          process(a);
          return a;
        },
        //把普通二维数组(全部由1，0表示)的转换成a*所需要的点数组
        convertArrToAS:function(arr)
        {
          var r = arr.length,c=arr[0].length;
          var a = new Array(r);
          for(var i=0;i<r;i++)
           {
              a[i] = new Array(c);
              for(var j=0;j<c;j++)
               {
                 var pos = new MapUtil.Point(i,j);
                 pos.flag = arr[i][j];
                 a[i][j]=pos;
               }
           }
          return a;
        },
        //A*算法,pathArr表示最后返回的路径
        findPathA:function(pathArr,start,end,row,col)
        {
         //添加数据到排序数组中
         function addArrSort(descSortedArr,element,compare)
            {
               var left = 0;
               var right = descSortedArr.length-1;
               var idx = -1;
               var mid = (left+right)>>1;
               while(left<=right)
               {
                  var mid = (left+right)>>1;
                  if(compare(descSortedArr[mid],element)==1)
                  {
                      left = mid+1;
                  }
                  else if(compare(descSortedArr[mid],element)==-1)
                  {
                      right = mid-1;
                  }
                  else
                  {
                      break;
                  }
               }
               for(var i = descSortedArr.length-1;i>=left;i--)
                {
                    descSortedArr[i+1] = descSortedArr[i];
                }
               descSortedArr[left] = element;
               return idx;
            }
         //判断两个点是否相同
         function pEqual(p1,p2)
         {
             return p1.x==p2.x&&p1.y==p2.y;
         }
         //获取两个点距离，采用曼哈顿方法
         function posDist(pos,pos1)
         {
           return (Math.abs(pos1.x-pos.x)+Math.abs(pos1.y-pos.y));
         }
         function between(val,min,max)
         {
           return (val>=min&&val<=max)
         }
         //比较两个点f值大小
         function compPointF(pt1,pt2)
         {
          return pt1.f-pt2.f;
         }
         //处理当前节点
         function processCurrpoint(arr,openList,row,col,currPoint,destPoint)
            {
               //get up,down,left,right direct
               var ltx = currPoint.x-1;
               var lty = currPoint.y-1;
               for(var i=0;i<3;i++)
                 for(var j=0;j<3;j++)
                   {
                      var cx = ltx+i;
                      var cy = lty+j;
                      if((cx==currPoint.x||cy==currPoint.y)&&between(ltx,0,row-1)&&between(lty,0,col-1))
                        {
                           var tp = arr[cx][cy];
                           if(tp.flag == 0 && tp.state!=1)
                             {
                               if(pEqual(tp,destPoint))
                               {
                                  tp.parent = currPoint;
                                  return true;
                               }
                               if(tp.state == -1)
                                {
                                   tp.parent = currPoint;
                                   tp.g= 1+currPoint.g;
                                   tp.h= posDist(tp,destPoint);
                                   tp.f = tp.h+tp.f;
                                   tp.state = 0
                                   addArrSort(openList,tp,compPointF);
                                }
                               else
                                {
                                   var g = 1+currPoint.g
                                   if(g<tp.g)
                                   {
                                      tp.parent = currPoint;
                                      tp.g = g;
                                      tp.f = tp.g+tp.h;
                                      openList.quickSort(compPointF);
                                   }
                                }
                             }
                        }
                   }
                return false;
            }
         //定义openList
         var openList = [];
         //定义closeList
         var closeList = [];
         start = pathArr[start[0]][start[1]];
         end = pathArr[end[0]][end[1]];
         //添加开始节点到openList;
         addArrSort(openList,start,compPointF);
         var finded = false;
         var tcount = 0;
         while((openList.length>0))
         {
           var currPoint = openList.pop();
           currPoint.state = 1;
           closeList.push(currPoint);
           finded = processCurrpoint(pathArr,openList,row,col,currPoint,end);
           if(finded)
           {
              break;
           }
         }
         if(finded)
         {
            var farr = [];
            var tp = end.parent;
            farr.push(end);
            while(tp!=null)
              {
                 farr.push(tp);
                 tp = tp.parent;
              }
            return farr;
         }
         else
         {
            return null;
         }
        }
    }

　　运用上面的代码，我们可以实现一个简单的迷宫寻路DEMO，用户在迷宫中点击任意的地点，蓝色的球体就会自动寻路移动到该点，如图：

　　此DEMO的源码地址

　　A*算法不仅可以应用在游戏当中，同样也可以应用到其他领域，比如车辆定位和行车自动导航，当然，这得需要另外的地理信息数据支持。

作者：马三小伙儿
出处：http://www.cnblogs.com/msxh/p/5674417.html 
请尊重别人的劳动成果，让分享成为一种美德，欢迎转载。另外，文章在表述和代码方面如有不妥之处，欢迎批评指正。留下你的脚印，欢迎评论！