浅谈FFT(快速傅里叶变换)

本文主要简单写写自己在算法竞赛中学习FFT的经历以及一些自己的理解和想法。

FFT的介绍以及入门就不赘述了，网上有许多相关的资料，入门的话推荐这篇博客：FFT（最详细最通俗的入门手册），里面介绍得很详细。

为什么要学习FFT呢？因为FFT能将多项式乘法的时间复杂度由朴素的$O(n^2)$降到$O(nlogn)$，这相当于能将任意形如$f[k]=\sum\limits _{i+j=k}f[i]\cdot f[j]$的转移方程的计算在$O(nlogn)$的时间内完成。因此对于想要进阶dp的同学来说，FFT是必须掌握的技能之一。（虽然在赛场上可能没什么用武之地）

我学习FFT的过程也是比较曲折的，从接触到真正理解它的原理前前后后经历了半年的时间。（实际上我从去年接触了FFT之后就一直把它当做一个黑盒算法来用，研究的事就扔到一边了，只是偶尔简单推算过几次公式，直到这个月初才开始深入学习它的原理）

由于本人才疏学浅，所以自己的叙述若存在一些错误或者不足之处，敬请读者指正。

首先FFT的作用是什么？可以将多项式的系数表达式转化成点值表达式（或者反过来，方法都是一样的）。FFT(a,n)的作用是将多项式a(系数表达式)从$w_{n}^{0}$到$w_{n}^{n-1}$的所有根对应的取值求出来。也就是说，设$f(x)=\sum\limits_{i=0}^{n-1}a[i]\cdot x^i$，经过FFT变换后，a[i]变成了$f(w_{n}^{i})$。

这个利用单位根来表示的点值表达式的一个好处是如果已知FFT(a0,n/2)以及FFT(a1,n/2)（a0为a的偶数次项所构成的多项式，a1为a的奇数次项所构成的多项式），则根据性质$\left\{\begin{matrix}\begin{aligned}&a[i]=a_0[i]+w_{n}^{i}\cdot a_1[i]\\&a[i+\frac{n}{2}]=a_0[i]-w_{n}^{i}\cdot a_1[i]\end{aligned} \end{matrix}\right.$可以在$O(n)$的时间内算出数组a的值。

为什么要用单位根呢？因为对于任意的数组长度n，在FFT的过程中使用单位根都只需要计算n个不同变量的值，与数组长度是线性相关的，而且一定能保证取到n个不同的值。而假如取2,3,4这样的数的话，在对任意子数组进行FFT时仍需计算n个不同变量的值，这样的话总的复杂度仍为$O(n^2)$，没有丝毫降低。而假如取-1，1这样的数，虽然只需要计算常数个变量的值了，但无论如何只能取到一两个变量的值，也就是只能确定两点，无法确定一个具有n个维度的多项式。

接下来就是代码实现了。

首先我们做一下预处理：

 typedef double db;
 const db pi=acos(-);

把double定义成db的作用，一是可以简化代码，二是需要调整精度的时候可以很方便地替换成其他变量类型，比如long double。

FFT的运算要用到复数，这就意味着我们必须找到一个能够代表复数的变量类型。图方便的话，C++库中内置的complex类就够用了。不过还是推荐自己写一个结构体，比C++自带的要快很多，而且也很好写。

由于复数是一个二元组，和二维平面上的点非常类似，因此可以直接套用二维几何中的点的结构体代码。加减数乘等操作都完全一样，只是多了个乘法。但这并不影响它的几何意义，因为在计算几何中两向量乘法我一般喜欢用dot(点积)和cross(叉积)两个函数来表示。此外，乘法运算符也可以表示坐标的旋转。

复数(点)的结构体代码如下：

 struct P {
     db x,y;
     P operator+(const P& b) {return {x+b.x,y+b.y};}
     P operator-(const P& b) {return {x-b.x,y-b.y};}
     P operator*(const P& b) {return {x*b.x-y*b.y,x*b.y+y*b.x};}
     P operator/(db b) {return {x/b,y/b};}
 }

接下来就是FFT的实现了。有了FFT的基本概念和点的表示方法之后，我们不难写出这样的代码：（f为1代表正变换（取值），f为1代表逆变换（插值））

 void FFT(P* a,int n,int f) {
     if(n==)return;
     static P b[N];
     for(int i=; i<n; i+=)b[i/]=a[i],b[(i+n)/]=a[i+];
     for(int i=; i<n; ++i)a[i]=b[i];
     FFT(a,n/,f),FFT(a+n/,n/,f);
     P wn= {cos(*pi/n),f*sin(*pi/n)},w= {,};
     for(int i=; i<n/; ++i,w=w*wn) {
         P x=a[i],y=w*a[i+n/];
         a[i]=x+y,a[i+n/]=x-y;
     }
 }

可以看出，这个代码是递归式的，其基本思想是将数组a分成两部分，偶数次项放在左半边，奇数次项放在右半边，然后对左右两部分分别递归做同样的处理，最后把两部分的答案合并，合并后a[0]-a[n-1]中的值分别为$f(w_{n}^{0})$-$f(w_{n}^{n-1})$的值。

但是递归在速度方面毕竟是硬伤，因此我们希望能将递归换成迭代的形式，这样速度会快很多。

通过观察，我们不难发现，FFT的第一步总是将a[i]与a[i+n/2]合并，每个多项式相邻两项在数组中的距离为n（即只有一项），而最后一步总是将a[i]与a[i+1]合并，每个多项式相邻两项的距离为2，中间每合并一轮，距离减半。经过一番观察和推理之后，我们可以得到如下改进后的代码：

 void FFT(P* a,int n,int f) {
     static P b[N];
     P *A=a,*B=b;
     for(int k=n; k>=; k>>=,swap(A,B))
         for(int i=; i<k>>; ++i) {
             P wn= {cos(pi*k/n),f*sin(pi*k/n)},w= {,};
             for(int j=i; j<n; j+=k,w=w*wn) {
                 P x=A[j],y=w*A[j+(k>>)];
                 B[((j-i)>>)+i]=x+y,B[((j-i)>>)+(n>>)+i]=x-y;
             }
         }
     if(A!=a)for(int i=; i<n; ++i)a[i]=A[i];
     if(!~f)for(int i=; i<n; ++i)a[i]=a[i]/n;
 }

这样我们就成功地去掉了递归，换成了迭代实现的版本。中间使用了两个指针A,B，是用乒乓效应减少数组的复制次数，有点类似倍增求后缀数组的方法。

但是这样虽然去掉递归了，但仍需要$O(n)$的辅助空间，而且如果迭代次数为奇数次的话，最后还需要把变换后的数组复制回原数组，不太美观。可以把辅助空间去掉，直接在原数组上进行合并吗？

对于上述代码，假设我们把x+y,x-y的值分别直接赋给a[((j-i)>>1)+i]和a[((j-i)>>1)+(n>>1)+i]，那么原来这两个位置上的信息就消失了，而这些信息在后面的合并中可能还需要用到，赋给其他位置也是同理。因此不能直接在原数组上进行赋值。这意味着，如果想直接在原数组上进行合并，合并后的两个值和合并前的两个值所存放的位置必须相同。例如，假如我们要合并下标分别为{0,4,8,12}和{2,6,10,14}的两个数组，那么a[0]+w*a[2]的值必须放在a[0]或者a[2]的位置，a[0]-w*a[2]的值则必须放在另一个对应的位置。这样一来，顺序会变得很乱（自己试一试就知道了），因此若想在合并后不改变原数组中各项的位置，就必须在合并前把原数组“打乱”（当然不是随便打乱，是对原数组进行一定规则的变换）。

如何“打乱”呢？我们可以把合并的过程倒过来观察一下，这里借用一下网络上的一张图：

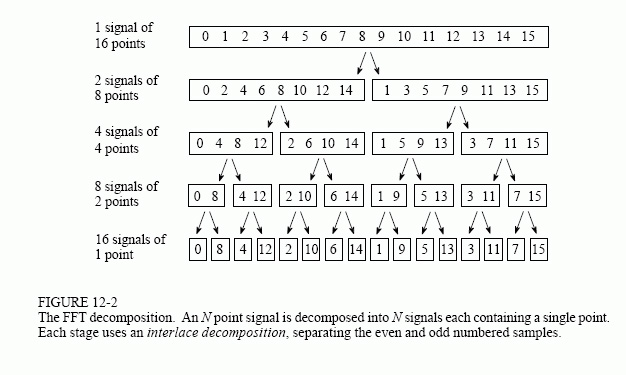
如图所示，我们把“合并”的过程看成是倒过来“拆分”的过程，这是其中一种拆分的方法，可以发现，这种拆分的方法能保证“任意两个位置上的数进行合并后的结果仍保存在它们各自的位置上，且合并后原数组的顺序不变”，这样就可以直接在原数组上进行合并了。

这种拆分方法有什么规律呢？同样也可以发现，第一次拆分后，偶数次项都被分到了左边，而奇数次项都分到了右边。第二次拆分后，把每个项的次数都除以二（向下取整），得到的数为偶数的继续被分到左边，为奇数则被分到右边，同理第三次拆分后要把每个项的次数除以4，第四次除以8......以此类推。从而我们可以总结出规律：设$n=2^t$，$rev(i)$为原数组的位置i拆分后对应的下标，$b(i,k)$为数字i的二进制第k位上的数(k∈{0,1})，利用按位累加的方法可以得到：

$b(rev(i),t-1-k)=\left\{\begin{matrix}\begin{aligned}0,b(i,k)=0\\ 1,b(i,k)=1\end{aligned}\end{matrix}\right.$

这相当于，每个数的拆分后的二进制第k位和原来的第t-1-k位是相同的，相当于把这个数的前t位二进制位进行了反转。

如何利用数组拆分后，对应的下标二进制反转的特性来对数组重排呢？一种比较普遍的方法是利用递推的方法求出原数组反转后的rev数组（方法不再叙述，网络上一搜便知），再从前往后扫一遍原数组，遇到rev数组中对应的元素比它小的情况，就交换一次。这种方法的时间复杂度是$O(n)$的，但仍需要$O(n)$的辅助空间，而且对于不同的n要重新求一遍rev数组，比较麻烦。直到我找到了这样的一段代码：

 void change(P* a,int n) {
     for(int i=,j=n>>,k; i<n-; ++i) {
         if(i<j)swap(a[i],a[j]);
         k=n>>;
         while(j>=k)j-=k,k>>=;
         j+=k;
     }
 }

这段代码打眼一看可能会有点懵逼，这是在干嘛？其实自己模拟一下便知，这是在对一个数组“暴力”进行反转，方法是模拟“倒过来加”的过程，把左起第一个0变成1，把前面的1都变成0，这样倒过来看就好像是整个数加了1，从头到尾扫一遍就行了。甚至可以改写成位运算的形式：

 void change(P* a,int n) {
     for(int i=,j=n>>,k; i<n-; ++i,j^=k) {
         if(i<j)swap(a[i],a[j]);
         for(k=n>>; j&k; j^=k,k>>=);
     }
 }

这样一来，FFT的空间消耗就彻底变成$O(1)$了。但是还有一个问题，就是这个函数的时间复杂度是多少呢？

可以看出，这个函数的时间复杂度主要取决于k的移动次数。不考虑边界情况的话，假如j的第一个0在第n-1位，那么k只需要移动一次（赋值成n/2），这样的情况一共有n/2种；假如第一个0在第n-2位，那么k需要移动两次，这样的情况一共有n/4种...以此类推。最坏的情况是第一个0在第0位，此时需要移动logn次，但这只有一种情况。

因此，假设$n=2^t$,则函数中的k总共需要移动$\sum\limits_{i=1}^ti\cdot 2^{t-i}$次。

这个式子怎么算呢？

我们考虑等比级数$\sum\limits_{i=1}^tx^{t-i+1}=\frac{x(1-x^t)}{1-x}$

等式两边求导得$\sum\limits_{i=1}^t(t-i+1)x^{t-i}=\frac{1-(t+1)x^t+tx^{t+1}}{(1-x)^2}$

又有$\sum\limits_{i=1}^t(t-i+1)x^{t-i}=(t+1)\sum\limits_{i=1}^tx^{t-i}-\sum\limits_{i=1}^tix^{t-i}$

即$\sum\limits_{i=1}^tix^{t-i}=(t+1)\sum\limits_{i=1}^tx^{t-i}-\sum\limits_{i=1}^t(t-i+1)x^{t-i}=\frac{(t+1)(1-x^t)}{1-x}-\frac{1-(t+1)x^t+tx^{t+1}}{(1-x)^2}$

将x=2代入得$\sum\limits_{i=1}^ti\cdot 2^{t-i}=\frac{(t+1)(1-2^t)}{1-2}-\frac{1-(t+1)2^t+t2^{t+1}}{(1-2)^2}$

化简得$\sum\limits_{i=1}^ti\cdot 2^{t-i}=2^{t+1}-t-2=2n-logn-2=O(n)$

对，你没有看错，空间复杂度降到了$O(1)$，而时间复杂度仍为$O(n)$，刺不刺激？

经过多次优化，可以最终得到了如下的FFT代码：

 void FFT(P* a,int n,int f) {
     for(int i=,j=n>>,k; i<n-; ++i,j^=k) {
         if(i<j)swap(a[i],a[j]);
         for(k=n>>; j&k; j^=k,k>>=);
     }
     for(int k=; k<n; k<<=) {
         P wn= {cos(pi/k),f*sin(pi/k)};
         for(int i=; i<n; i+=k<<) {
             P w= {,};
             for(int j=i; j<i+k; ++j,w=w*wn) {
                 P x=a[j],y=w*a[j+k];
                 a[j]=x+y,a[j+k]=x-y;
             }
         }
     }
     if(!~f)for(int i=; i<n; ++i)a[i]=a[i]/n;
 }

非递归实现，$O(nlogn)$的时间复杂度，O(1)的空间复杂度，既保证了效率又简洁了代码，岂不美哉？

有了FFT的代码，就可以实现多项式乘法了。用FFT实现多项式乘法的一般步骤是将被乘的两个多项式分别用FFT转化成点值表达式，然后对应位相乘，最后再用FFT逆变换转化回来就行了。

值得注意的是，对被乘的两个多项式进行FFT时，数组长度至少应大于两个多项式的最高次数之和，否则会出现莫名其妙的错误。又因为数组长度必须是2的t次方的形式，保险起见最好开到多项式相乘后的最高次数的两倍或以上。

最后推荐几道FFT的练习题：

HDU - 4609 3-idiots

UVA - 12298 Super Poker II

Gym - 101002E K-Inversions

Gym - 101667H Rock Paper Scissors

HDU - 1402 A * B Problem Plus

Gym - 101234D Forest Game

顺便附上UVA - 12298的完整代码：

 #include<bits/stdc++.h>
 using namespace std;
 typedef long long ll;
 typedef long double db;
 const int N=2e5+;
 const db pi=acos(-);
 struct P {
     db x,y;
     P operator+(const P& b) {return {x+b.x,y+b.y};}
     P operator-(const P& b) {return {x-b.x,y-b.y};}
     P operator*(const P& b) {return {x*b.x-y*b.y,x*b.y+y*b.x};}
     P operator/(db b) {return {x/b,y/b};}
 } p[][N];
 void FFT(P* a,int n,int f) {
     for(int i=,j=n>>,k; i<n-; ++i,j^=k) {
         if(i<j)swap(a[i],a[j]);
         for(k=n>>; j&k; j^=k,k>>=);
     }
     for(int k=; k<n; k<<=) {
         P wn= {cos(pi/k),f*sin(pi/k)};
         for(int i=; i<n; i+=k<<) {
             P w= {,};
             for(int j=i; j<i+k; ++j,w=w*wn) {
                 P x=a[j],y=w*a[j+k];
                 a[j]=x+y,a[j+k]=x-y;
             }
         }
     }
     if(!~f)for(int i=; i<n; ++i)a[i]=a[i]/n;
 }
 int com[N],a,b,c;

 int main() {
     memset(com,,sizeof com);
     for(int i=; i<N; ++i)if(!com[i])for(int j=i*; j<N; j+=i)com[j]=;
     while(scanf("%d%d%d",&a,&b,&c)&&(a||b||c)) {
         int m;
         for(m=; m<=b*; m<<=);
         for(int f=; f<; ++f)fill(p[f],p[f]+m,(P) {,});
         while(c--) {
             int x;
             char ch;
             scanf("%d%c",&x,&ch);
             if(x>b)continue;
             if(ch=='S')p[][x].x--;
             else if(ch=='H')p[][x].x--;
             else if(ch=='C')p[][x].x--;
             else if(ch=='D')p[][x].x--;
         }
         for(int f=; f<; ++f)
             for(int i=; i<=b; ++i)p[f][i].x+=com[i];
         for(int i=; i<; ++i)FFT(p[i],m,);
         for(int f=; f<; ++f) {
             FFT(p[],m,);
             for(int i=; i<m; ++i)p[][i]=p[][i]*p[f][i];
             FFT(p[],m,-);
             for(int i=b+; i<m; ++i)p[][i]= {,};
         }
         for(int i=a; i<=b; ++i)printf("%lld\n",ll(p[][i].x+0.5));
         puts("");
     }
     return ;
 }