北京DAY1下午

省选模拟题

周子凯

题目概况

中文题目名	简易比特币	计算	路径
英文题目名	bit	calculation	Path
输入文件名	bit.in	calculation.in	path.in
输出文件名	bit.out	calculation.out	path.out
每个测试点时限	1s	2s	1s
内存限制	128M	128M	128M
测试点数目	10	10	10
每个测试点分值	10	10	10
结果比较方式	全文比较（过滤行末空格及文末回车）
题目类型	传统

1. 简易比特币

题目描述

相信大家都听说过比特币。它是一种虚拟货币，但与普通虚拟货币不同的是，它不由某个机构统一发行，而需要利用计算机找出具有特定性质的数据来“发现”货币，俗称“挖矿”。然而，由于具有这种特定性质的数据分布稀疏而无规律，因此挖矿的过程需要投入大量的计算资源来搜寻这些数据。

仿照比特币是设计思想，我们可以设计一种简易的比特币：给定一个由n个非负整数构成的序列{a_i}，和一个阈值K，如果某个非空子序列（一个连续的区间）中的所有数的异或和小于K，则这个子序列就对应了一个比特币，否则它毫无价值。

现在，给出这个序列和阈值，请你计算从中能获得多少个比特币。

严谨起见，简要解释一下什么是异或：

异或是一种位运算，Pascal中写作xor，C/C++中写作^。将两个数写成二进制形式，然后对每位作“相同得0、不同得1”的运算。例如，12 xor 6 = 10的运算方法如下：

12 = (1100)₂

6   = (0110)₂

ans= (1010)₂ = 10

输入格式

第一行包含两个整数n和K，意义如题所述；

第二行包含n个非负整数a_i，表示序列中的每一个数。

输出格式

一行包含一个整数，表示能从序列中获得的比特币数。

样例输入

3 2

1 3 2

样例输出

3

样例解释

1 = 1

1 xor 3 = 2

1 xor 3 xor 2 = 0

3 = 3

3 xor 2 = 1

2 = 2

一共3个区间的异或和小于2。

数据范围

对于20%的数据，n≤100；

对于40%的数据，n≤1000；

另有20%的数据，a_i≤50；

对于100%的数据，1≤n≤10⁵，0≤K≤10⁹，0≤a_i≤10⁹。

2.计算

问题描述

我曾经的竞赛教练有一句名言：“人紧张起来的时候会变得和白痴一样的。”他总爱在比赛前重复这句话。其实论算法，他并没有教给我们多少，但是回想起以前的经历发现，至少这句话他说的真是太tm对了。用现在的话讲就是：不要怂，就是干。

oi题很多时候都是这样，乍一看很难，越看越觉得不可做，于是安慰自己说，肯定又是我没学过的某算法，做不出很正常。但抱有这种心理的，出了考场往往会被身边的神犇打脸：“这题其实先oo一下再xx一下就好了，我太弱了搞了一小时才搞出来……”

现在就有一道看上去似乎很不好搞的计算题，请你不怂地算一下怎么搞。

给出一个长为N的正整数序列，有三种操作：

A l r k b：在区间[l,r]上加上一个首项为b、公差为k的等差数列。即，序列a_l, a_l+1, a_l+2, a_l+3……变成a_l+b, a_l+1+b+k, a_l+2+b+2k, a_l+3+b+3k……

B l r：求区间[l,r]内所有数的和mod 1000000007的值

C l r：求区间[l,r]内所有数的平方的和mod 1000000007的值

输入格式

第一行包含两个数n、q，表示序列长度和操作的数量；

第二行包含n个数{a_i}，表示原序列；

接下来q行，每行包含一个操作，格式和意义如题面所述。

输出格式

输出若干行，每个B操作和C操作输出一行，表示询问的答案。

样例输入

3 3

1 1 1

A 1 3 2 2

B 1 2

C 2 3

样例输出

8

74

数据规模

测试点1~2：n, q ≤ 1000；

测试点3~4：k=0，没有C操作；

测试点5~6：k=0；

测试点7~8：没有C操作；

对于100%的数据，n, q ≤ 100000，0 ≤ a_i, k, b ≤ 10⁹，1 ≤ l ≤ r ≤ n

3. 路径

问题描述

实在不知道怎么编题面了，就写得直白一点吧。反正没几个人写得完三题，估计都看不到这里。

给出一个仙人掌图，求图中最长路的长度。

Emmm……还是稍微具体一点吧。

仙人掌图是指一个有N个点与M条边的无向图，点从1到N标号，每条边有各自的长度，图中可能存在若干个简单环，但是，每个点最多只会属于1个简单环路。简单环是指一个经过至少两个点、且不经过重复点的环。（这里仙人掌图的定义也许和你在别处见过的不太一样，请仔细审题）

例如，图1所示的是一个仙人掌图，但图2则不是，因为3号点同属于两个简单环。

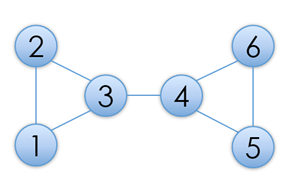
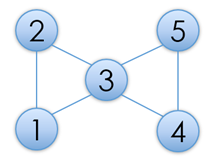
给出一个仙人掌图，你需要求出图中的最长路的长度。最长路不能经过重复的点。例如，假设图中所有边长度都为1的话，图1中的仙人掌图的一条最长路为1-2-3-4-5-6，长度为5。

输入格式

       第一行包含1个整数Q，表示数据组数；

每组数据的第一行2个整数N,M，表示仙人掌图的点数和边数；

每组数据的接下来M行，每行3个正整数x,y,z，描述一条连接点x与点y，长度为z的边。

输出格式

对于每组数据输出一行，每行包含一个整数，表示最长路径的长度。

样例输入

2

6 7

1 2 1

2 3 1

3 1 1

3 4 1

4 5 1

5 6 1

6 4 1

4 4

1 2 1

2 3 2

3 4 3

4 1 4

样例输出

5

9

数据规模

对于10%的数据，Q ≤ 5，n ≤ 10；

另有20%的数据，满足n=m+1；

另有20%的数据，满足n=m；

另有20%的数据，满足每个环上的点数≤ 20；

对于100%的数据，Q ≤ 1000, 所有测试点的n之和 ≤ 100,000，z≤ 1000。

(T3图片可能被河蟹，没有就算了hhh)

今天T1就是Trie树上异或乱搞，T2玄学线段树标记应用(区间加等差数列，区间查询元素和和元素平方和)。

T3还没讲，，，(我明明写的50分暴力分啊，，，怎么多骗了20分hhh)

先粘一下我的代码

T1:

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<algorithm>
#define ll long long
#define maxn 100005
using namespace std;
int n,k,ch[maxn*][],siz[maxn*];
int tot=,val,now,ci[],root=;
ll ans=;

inline int read(){
    int x=;char c=getchar();
    for(;!isdigit(c);c=getchar());
    for(;isdigit(c);c=getchar()) x=x*+c-'';
    return x;
}

inline void ins(){
    int pos=root,r;
    siz[]++;

    for(int i=;i>=;i--){
        r=(ci[i]&now)?:;
        if(!ch[pos][r]) ch[pos][r]=++tot;
        pos=ch[pos][r],siz[pos]++;
    }
}

inline int query(){
    int pos=root,an=,r;
    for(int i=;i>=;i--) if(k&ci[i]){
        r=(now&ci[i])?:;
        if(ch[pos][r]) an+=siz[ch[pos][r]];
        pos=ch[pos][r^];
        if(!pos) break;
    }else{
        pos=ch[pos][(now&ci[i])?:];
        if(!pos) break;
    }

    return an;
}

int main(){
    freopen("bit.in","r",stdin);
    freopen("bit.out","w",stdout);

    ci[]=;
    for(int i=;i<=;i++) ci[i]=ci[i-]<<;
    n=read(),k=read();
    now=,ins();
    for(int i=;i<=n;i++){
        val=read();
        now^=val;
        ans+=(ll)query();
        ins();
    }

    cout<<ans<<endl;
    return ;
}

T2:

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<algorithm>
#define ll long long
#define maxn 400005
#define ha 1000000007
using namespace std;
ll hd[maxn],tag[maxn];
ll sum[maxn],sum_t[maxn];
ll sum_c[maxn],n,m,a[maxn>>];
int le,ri,opt;
ll k,b,pos,ans;
char ch;
bool ww;

inline void pushup(int o,int lc,int rc,ll len){
    sum[o]=sum[lc]+sum[rc];
    if(sum[o]>=ha) sum[o]-=ha;
    sum_t[o]=sum_t[lc]+sum_t[rc];
    if(sum_t[o]>=ha) sum_t[o]-=ha;
    sum_c[o]=(sum_c[lc]+sum_c[rc]+sum[rc]*len)%ha;
}

void build(int o,int l,int r){
    if(l==r){
        sum[o]=a[l],sum_t[o]=a[l]*a[l]%ha;
        return;
    }

    int mid=(l+r)>>,lc=o<<,rc=(o<<)|;
    build(lc,l,mid),build(rc,mid+,r);
    pushup(o,lc,rc,mid+-l);
}

inline ll ci1(ll x){
    if(!x) return ;
    return x*(x+)/%ha;
}

inline ll ci2(ll x){
    if(!x) return ;
    ll an=x*(x+)>>1ll;
    if(!(an%)) return an/%ha*(x*+)%ha;
    else return (*x+)/*(an%ha)%ha;
}

inline void change(int o,ll len,ll sx,ll gc){
    hd[o]=(hd[o]+sx)%ha,tag[o]=(tag[o]+gc)%ha;
    sum_t[o]=(sum_t[o]+len*sx%ha*sx%ha+gc*gc%ha*ci2(len-)%ha+2ll*sx%ha*sum[o]%ha)%ha;
    sum_t[o]=(sum_t[o]+2ll*sx%ha*gc%ha*ci1(len-)%ha+2ll*gc%ha*sum_c[o]%ha)%ha;
    sum[o]=(sum[o]+sx*len%ha+ci1(len-)*gc)%ha;
    sum_c[o]=(sum_c[o]+ci1(len-)*sx%ha+gc*ci2(len-))%ha;
}

inline void pushdown(int o,int l,int r){
    if(hd[o]||tag[o]){
        int mid=(l+r)>>,lc=o<<,rc=(o<<)|;
        change(lc,mid-l+,hd[o],tag[o]);
        change(rc,r-mid,(hd[o]+tag[o]*(mid+-l))%ha,tag[o]);
        hd[o]=tag[o]=;
    }
}

void update(int o,int l,int r){
    if(l>=le&&r<=ri){
        change(o,r-l+,(b+(ll)(l-le)*k)%ha,k);
        return;
    }

    pushdown(o,l,r);
    int mid=(l+r)>>,lc=o<<,rc=(o<<)|;
    if(le<=mid) update(lc,l,mid);
    if(ri>mid) update(rc,mid+,r);
    pushup(o,lc,rc,mid+-l);
}

ll query1(int o,int l,int r){
    if(l>=le&&r<=ri) return sum[o];
    pushdown(o,l,r);
    ll an=,mid=(l+r)>>,lc=o<<,rc=(o<<)|;
    if(le<=mid) an+=query1(lc,l,mid);
    if(ri>mid) an+=query1(rc,mid+,r);
    if(an>=ha) an-=ha;
    return an;
}

ll query2(int o,int l,int r){
    if(l>=le&&r<=ri) return sum_t[o];
    pushdown(o,l,r);
    ll an=,mid=(l+r)>>,lc=o<<,rc=(o<<)|;
    if(le<=mid) an+=query2(lc,l,mid);
    if(ri>mid) an+=query2(rc,mid+,r);
    if(an>=ha) an-=ha;
    return an;
}

int main(){
    freopen("calculation.in","r",stdin);
    freopen("calculation.out","w",stdout);

    scanf("%lld%lld",&n,&m);
    for(int i=;i<=n;i++) scanf("%lld",a+i);
    build(,,n);
    while(m--){
        ch=getchar();
        while(ch>'C'||ch<'A') ch=getchar();
        if(ch=='A'){
            scanf("%d%d%lld%lld",&le,&ri,&k,&b);
            update(,,n);
        }else if(ch=='B'){
            scanf("%d%d",&le,&ri);
            printf("%lld\n",query1(,,n));
        }else{
            scanf("%d%d",&le,&ri);
            printf("%lld\n",query2(,,n));
        }
    }
    return ;
}

T3:

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<algorithm>
#define ll long long
#define maxn 100005
using namespace std;
int n,m,T,st[maxn],tp,tot_len;
int tot,cirpot[maxn],mx1,mx2;
int to[maxn*],val[maxn*],ne[maxn*];
int hd[maxn],dis[maxn],num,ans;
bool v[maxn],is_cc[maxn],hhh;

inline void init(){
    num=ans=tp=tot=tot_len=;
    hhh=;
    mx1=mx2=;
    memset(hd,,sizeof(hd));
    memset(dis,,sizeof(dis));
    memset(is_cc,,sizeof(is_cc));
    memset(v,,sizeof(v));
}

inline void add(int uu,int vv,int ww){
    to[++num]=vv,ne[num]=hd[uu],hd[uu]=num,val[num]=ww;
    to[++num]=uu,ne[num]=hd[vv],hd[vv]=num,val[num]=ww;
}

void dfs(int x,int len){
    ans=max(ans,len);
    v[x]=;
    for(int i=hd[x];i;i=ne[i]) if(!v[to[i]]) dfs(to[i],len+val[i]);
    v[x]=;
}

void tree_dp(int x,int fa){
    for(int i=hd[x];i;i=ne[i]) if(to[i]!=fa&&!is_cc[to[i]]){
        tree_dp(to[i],x);
        ans=max(ans,dis[x]+dis[to[i]]+val[i]);
        dis[x]=max(dis[x],dis[to[i]]+val[i]);
    }
}

void find_circle(int x,int fa){
    st[++tp]=x,v[x]=;
    for(int i=hd[x];i;i=ne[i]) if(to[i]!=fa&&!hhh){
        if(v[to[i]]){
            hhh=;
            int h;
            for(h=tp;h;h--) if(st[h]==to[i]) break;
            for(;h<=tp;h++) is_cc[st[h]]=,cirpot[++tot]=st[h];

        }
        else find_circle(to[i],x);
    }
    tp--;
}

int hh(int x){
    if(x==tot+) return ;
    for(int i=hd[cirpot[x]];i;i=ne[i]) if(to[i]==cirpot[x%tot+]) return val[i]+hh(x+);
    return ;
}

void get(int x,int dd){
    tree_dp(cirpot[x],);
    ans=max(ans,max(dis[cirpot[x]]+mx1+dd,dis[cirpot[x]]+mx2-dd));
    mx1=max(mx1,dis[cirpot[x]]-dd);
    mx2=max(mx2,tot_len+dis[cirpot[x]]+dd);
    if(x==tot) return;
    for(int i=hd[cirpot[x]];i;i=ne[i]) if(to[i]==cirpot[x+]) get(x+,dd+val[i]);
}

int main(){
    freopen("path.in","r",stdin);
    freopen("path.out","w",stdout);

    scanf("%d",&T);
    for(int l=;l<=T;l++){
        init();
        scanf("%d%d",&n,&m);
        int uu,vv,ww;
        for(int i=;i<=m;i++){
            scanf("%d%d%d",&uu,&vv,&ww);
            add(uu,vv,ww);
        }

        if(n>=m){
            if(n==m+) tree_dp(,);
            else{
                find_circle(,);
                tot_len=hh();
                get(,);
            }
        }else{
            for(int i=;i<=n;i++) dfs(i,);
        }

        printf("%d\n",ans);
    }

    return ;
}

T3竟然是找环之后单调队列？？？？

代码难度->INF

(神TM仙人掌，这个坑回来一定要填)