线段树简单入门

递归版线段树

线段树的定义

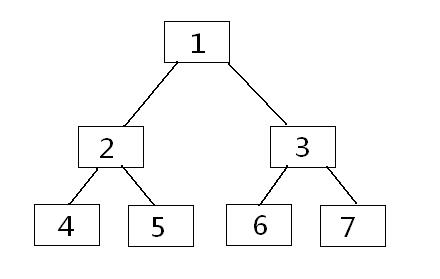
线段树, 顾名思义, 就是每个节点表示一个区间.

线段树通常维护一些区间的值, 例如区间和.

比如, 上图 $[2, 5]$ 区间的和, 为以下区间的和的和:

我们可以这样定义线段树的一个节点:

struct node {
    int sum; // 维护该节点表示区间的和
    int l, r; // 表示该节点表示的左右区间 (然而实现中常常不需要存储, 后面会说到)
    int lc, rc; // 表示该节点的左右孩子 (然而实现中常常不需要存储, 后面会说到)
};

实现中, 我们常常使用完全二叉树来表示线段树, (如果你写过二叉堆的话你会知道要如何表示) 而在完全二叉树中一个节点的左孩子右孩子可以很方便的求出.

(若线段树不是完全二叉树, 可以假装它是完全二叉树, 毕竟这样比较方便)

因为常常我们只需要存储一个值 sum, 于是下文只存储了一个数组 seg[] 代表所有节点的 sum 值.

线段树的基础操作

例题

Luogu 树状数组

已知一个数列，你需要进行下面两种操作：

将某一个数加上 $x$
求出某区间每一个数的和

$0 \le n \le 2\times 10^5$

更新节点

直接拿左孩子右孩子更新就可以了.

void Updata(int x) {
    seg[x] = seg[x << 1] + seg[x << 1 | 1];
}

建树

暴力建就可以了.

void Build(int x, int l, int r, int a[]) { // 给 a[] 数组建线段树
    if(l < r) {
        int mid = (l + r) >> 1;
        Build(x << 1, l, mid);
        Build(x << 1 | 1, mid + 1, r);
        Updata(x);
    } else seg[x] = a[l];
}

修改节点

递归修改, 然后更新.

// cur 表示我们目前查询到了的节点编号
// [l, r] 表示 cur 这个节点所表示的区间
// 将 a[q] 改为 k
void Modify(int cur, int l, int r, int q, int k) {
    if(l == r) {
        seg[cur] = k;
    } else {
        int mid = (l + r) >> 1; // 左右子树的区间分别为 [l, mid], [mid + 1, r]
        if(q <= mid) Modify(cur << 1, l, mid, q, k); // 要修改的节点在左孩子
        else Modify(cur << 1 | 1, mid + 1, r, q, k); // 要修改的节点在右孩子
        Updata(cur);
    }
}

查询区间和

// cur 表示我们目前查询到了的节点编号
// [l, r] 表示 cur 这个节点所表示的区间
// [ql, qr] 表示我们要查询的区间
int Query(int cur, int l, int r, int ql, int qr) {
    if(ql <= l && r <= qr) return seg[cur];
    // 如果这个节点表示区间被 [ql, qr] 包含, 就返回这个节点的值
    int mid = (l + r) >> 1, ret = 0; // 左右子树的区间分别为 [l, mid], [mid + 1, r]
    if(ql <= mid) ret += Query(cur << 1, l, mid, ql, qr);
    if(qr > mid) ret += Query(cur << 1 | 1, mid + 1, r, ql, qr);
    return ret;
}

线段树的懒标记 (lazy tag)

区间修改 (区间增加某数)

我们想做区间修改.

显然暴力修改的时间复杂度是在太奇怪了.

我们考虑每次修改的信息要查询非常多次, 可以使用 lazy tag.

具体做法是: 我们先不增加, 而是标记这个节点需要增加, 到之后再来增加.

比如, 下传是这样的:

void PushTag(int x) {
    tag[x << 1] += tag[x]; tag[x << 1 | 1] += tag[x];
    int mid = (l + r) >> 1;
    seg[x << 1] += (mid - l + 1) * tag[x]; // 左孩子为 [l, mid]
    seg[x << 1 | 1] += (r - mid) * tag[x]; // 右孩子为 [mid + 1, r]
    tag[x] = 0;
}

这样, 我们就可以写出来区间修改.

int Modify(int cur, int l, int r, int ql, int qr, int k) { // 区间 [ql, qr] 增加 k
    if(ql <= l && r <= qr) {
        seg[cur] += (r - l + 1) * k;
        tag[cur] += k;
    } else {
        PushTag(cur);
        int mid = (l + r) >> 1;
        if(ql <= mid) Modify(cur << 1, l, mid, ql, qr, k);
        if(qr > mid) Modify(cur << 1 | 1, mid + 1, r, ql, qr, k);
        Updata(cur);
    }
}

标记下传

每次访问节点都下传一下就可以了.

(此处用到了"均摊分析"的思想 (分析复杂度并不需要用均摊分析) )

暴力的时间复杂度到了哪里呢?

其实你可以发现: 每一次修改需要很多次查询才会把标记降完, 而再加上标记可以合并, 时间复杂度就为严格的 $O(n \log n)$.

线段树的动态开点

直接用指针实现即可, 这里不多赘述.

zkw 线段树

引入

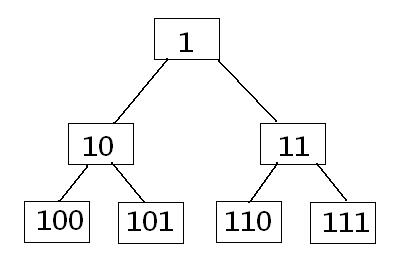
在我们写线段树的时候, 我们会发现:

化成二进制就是:

我们可以发现一些很有趣的性质, 我们可不可以自底向上做呢?

zkw 线段树的基础操作

建树

(因为后面操作的需要, 我们需要建立 $[0, n + 2)$ 的 zkw 线段树)

inline void Build() {
    for(M = 1; M < n + 2; M <<= 1);
    for(int i = M + 1; i <= M + n; i++) scanf("%d", seg + i); // 读入
    for(int i = M - 1; i; i--) Updata(i);
    // 更新所有值, 因为左右孩子编号一定比父亲的编号大, 所以父亲的孩子一定处理过
}

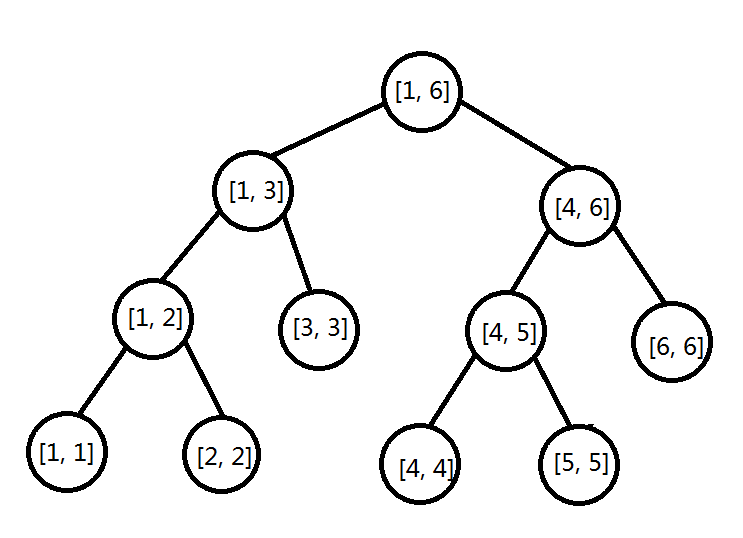
例如, 我们把 $[1, 9, 6, 2, 1, 0]$ 建树, 结果是这样的.

单点修改

可以发现会影响到的只会是要修改的节点的父亲, 直接更新父亲就可以了.

inline void Modify(int x, int v) {
    seg[x += M] += v;
    while(x) Updata(x >>= 1);
}

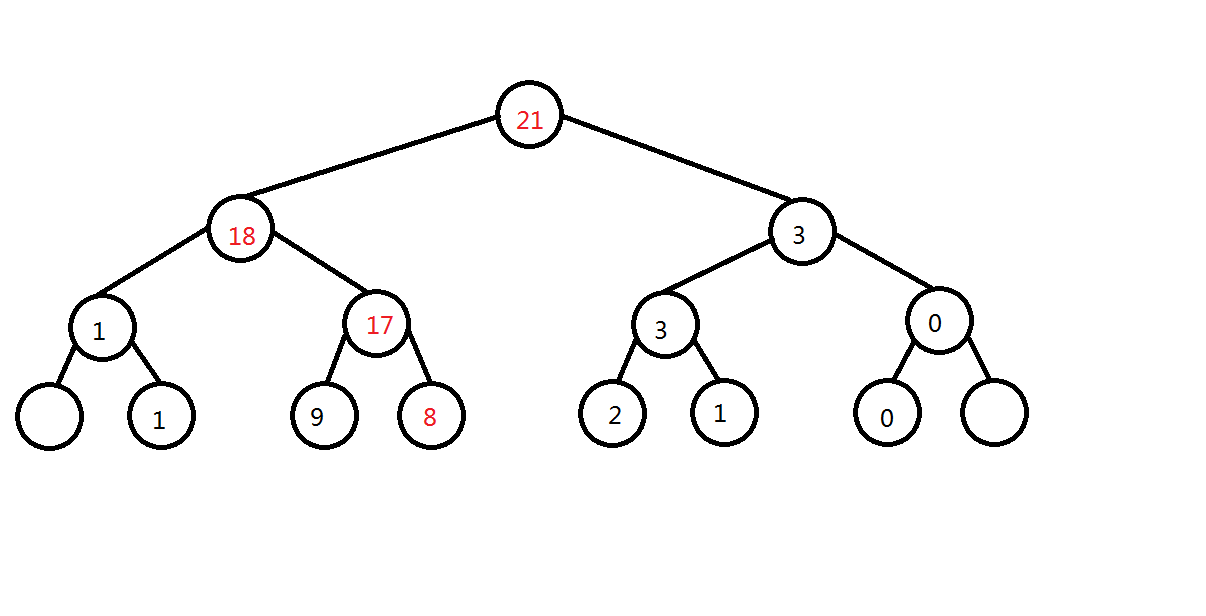
区间求和

我们先把开区间转化为闭区间. $[s, t] \to (s - 1, t + 1)$. (这就是我们需要开 $[0, n - 2$) 的原因)

假设我们需要统计的是红色方框内的东西.

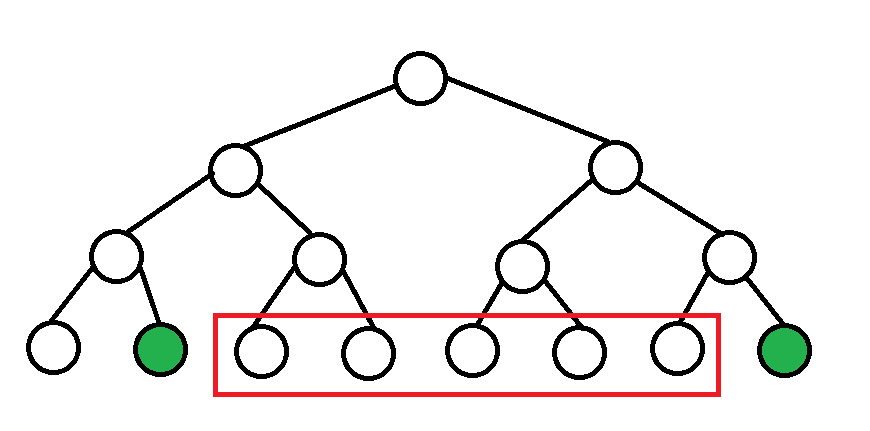
找出 $s - 1$ 和 $t + 1$ 的所有深度小于等于他们 LCA 的祖先, 可以发现:

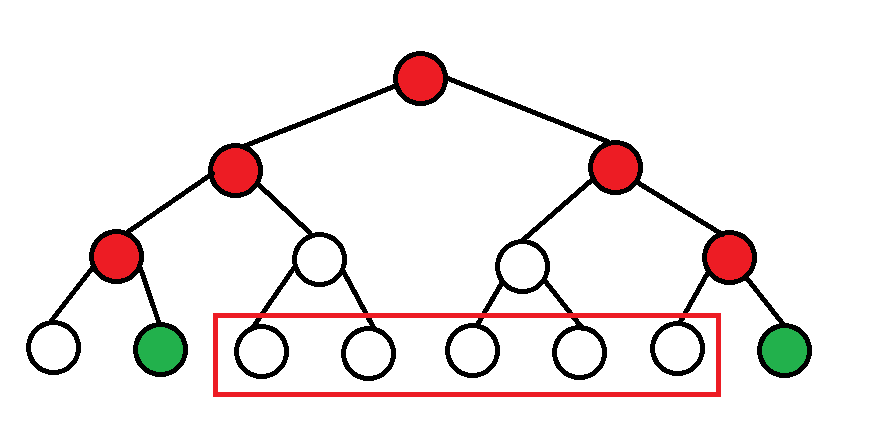
我们要查询的区间恰好被包裹!

所以我们可以考虑这样的操作:

$s \leftarrow s + M - 1, t \leftarrow t + M + 1$. (找到叶子结点, 并且设置为开区间)
若 $s$ 是左孩子, 则统计 $s$ 的父亲的右孩子的答案. (显然这个节点在答案里)
若 $t$ 是右孩子, 则统计 $t$ 的父亲的左孩子的答案. (显然这个节点也在答案里)
将 $s$ 与 $t$ 都变为它们各自的父亲.
若 $s$ 与 $t$ 不是兄弟, 回到 2.
此时答案已经统计完毕.

为什么不会多加呢? 因为只有在它们是兄弟的时候才会多加, 而是兄弟的时候就已经停止了.

其它可以根据模拟感性理解.

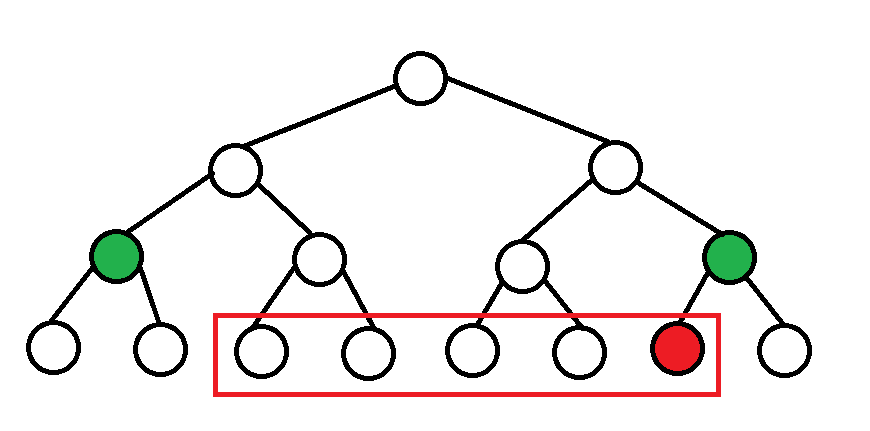
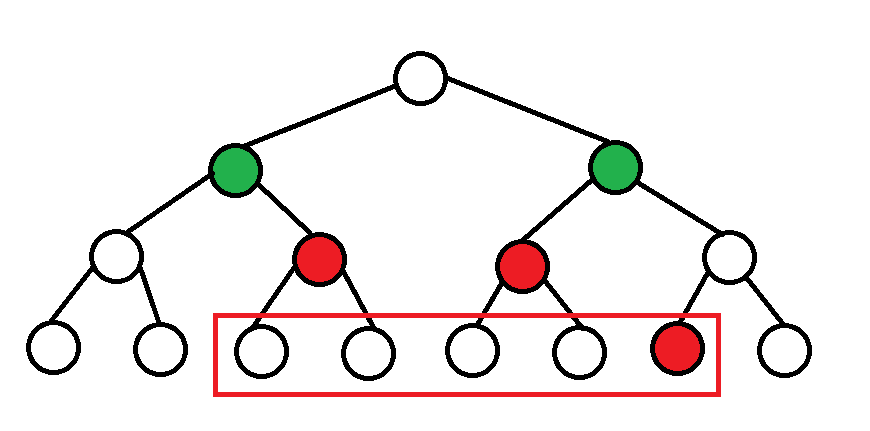
代码如下:

inline int Query(int s, int t, int ret = 0) {
    for(s += M - 1, t += M + 1; s ^ t ^ 1; s >>= 1, t >>= 1) {
        if(~s & 1) ret += seg[s + 1];
        if(t & 1) ret += seg[t - 1];
    }
    return ret;
}
## (可持久化线段树) 主席树
### 引入
如果我们要调用某一次修改之后的结果, 怎么做呢?
hjt 想出了一个非常好的办法 (据说是 hjt 考场上不会写划分树于是发明主席树) ~~到这里你应该知道这个名字是怎么来了的~~
### 函数式编程
函数式永远只做定义, 不做修改, 所以函数式编程自带可持久化.
### 主席树的基础操作
#### 单点修改
我们实际上只需要管修改就可以了.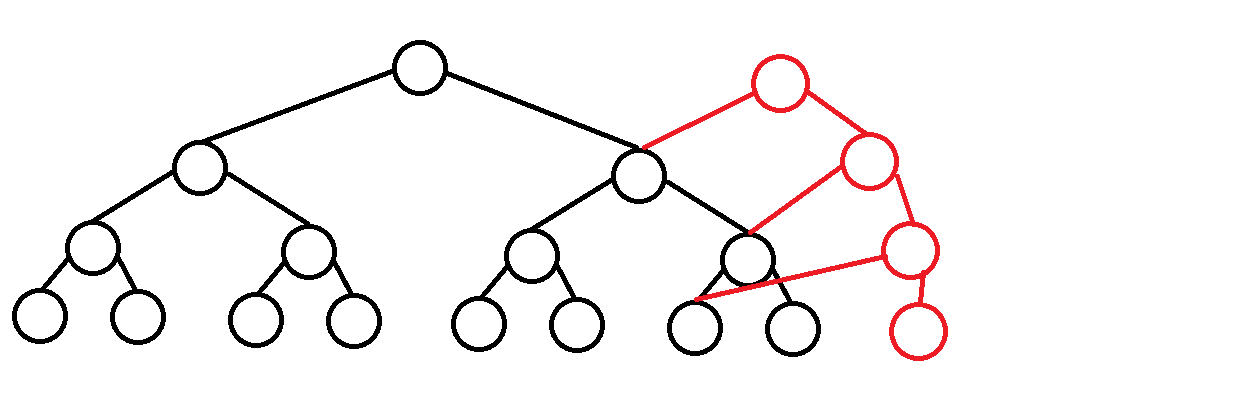
![yjhzkw4.png](https://i.loli.net/2019/02/28/5c7775065b31f.png)
对于每次修改一个节点, 我们都新建一个节点, 而不要修改原来的节点, 新建出来的节点和原来的节点的多数是一样的.
```cpp
node *NewNode(int val, node *lc, node *rc) {
    node *ptr = new node;
    ptr->lchild = lc; ptr->rchild = rc; ptr->val = val;
    return ptr;
}
void Modify(node *&cur, node *fa, int l, int r, int x) {
    cur = NewNode(fa->val + 1, fa->lchild, fa->rchild);
    if(l != r) {
        int mid = (l + r) >> 1;
        if(x <= mid) Modify(cur->lchild, cur->lchild, l, mid, x);
        else Modify(cur->rchild, cur->rchild, mid + 1, r, x);
    }
}

(其实主席树比线段树短?)

区间修改

由于主席树不便于标记下传，你可以使用标记永久化.

静态区间第 k 大

如果我们按原区间从左到右给编号为它的值的位置增加 $1$, 则我们可以用第 $r$ 个版本的某一个节点和减去第 $l - 1$ 个版本的同一节点 (是表示区间相同) 和得到区间内有多少个在范围内的数.

考虑整体二分.

因为线段树的结构刚好适合二分, 所以我们不用再写 query 了.

int Query(node *u, node *v, int l, int r, int k) {
    if(l == r) return l;
    int mid = (l + r) >> 1, m = v->lchild->val - u->lchild->val;
    if(m >= k)
        return Query(u->lchild, v->lchild, l, mid, k);
    else return Query(u->rchild, v->rchild, mid + 1, r, k - m);
}

结语

讲完了

祝大家身体健康