LeetCode343 整数拆分详解

题目详情

给定一个正整数 n，将其拆分为至少两个正整数的和，并使这些整数的乘积最大化。 返回你可以获得的最大乘积。

示例 1:

输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1。

示例 2:

输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。

说明: 你可以假设 n 不小于 2 且不大于 58。

题目解析

关键是找到状态方程， 我们设置dp[i]表示整数i的最大乘积， 那么把问题分成子问题， 我们发现dp[i] 与前面的dp[1] ~ dp[i-1]都有关系， 关系很容易找到

dp[i] = max(j * (i-j), j * dp[i - j])  j = 1,2 ······ i -1

而初始条件dp[1] = 1, dp[2] = 2, dp[3] = 3

为什么要加上 j * (i-j)的比较呢， 是为了处理dp[i] < i的情况， 例如

n=4， 那么如果不考虑 j * (i-j)， 因为dp[2] = 1 <2, 所以最终的结果为3， 但是其实把4分成2 * 2， 最终结果为4. 所以要加上 j * (i-j) 直接把i分成两个数字i, j-i,的情况。

那么可以由此得到第一种dp代码

代码一 动态规划

class Solution {
public:
    int integerBreak(int n) {
        vector <int> dp(n +1, 0);
        int tmp = 0;
        dp[0] = 0;
        dp[1] = 1;
        dp[2] = 1;

        for (int i = 3; i <= n ; i++) {
            tmp = 0;
            for (int j = 1; j <= i - 1; j++) {
                tmp = max(tmp, max(dp[j] * (i-j), j * (i - j)));
            }
            dp[i] = tmp;
        }

        return dp[n];
    }
};

时间复杂度为0(n^2)

代码2 数学推倒

有一些其他的博客给了更加速度快的算法， 有一种是利用数学推导， 得出要想使乘积最大， 只需要尽可能的多分成3， 其次是二

数学推导过程

由均值不等式(n个数的算术平均数大于等于它们的几何平均数)：

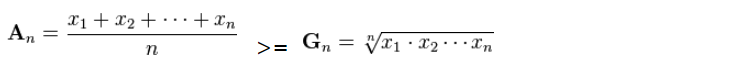
得：当把输入的n拆分成几个相等的数时它们的积最大。

那么问题来了，拆分成几个呢？

为了方便使用导数，我们先假设我们可以把n拆分成实数。那么设每一个数为x,则一共有n/x个数。

设它们的积为f(x),则f(x)=x(n/x)，那么怎么求f(x)最大值呢？求导数！

f′(x)=(n/x2) * x(n/x) * (1-lnx)

当x=e时取极大值。

而我们题目里规定x为整数，那么我们只需要取的x越靠近e越好。那么2<e<3，而且e=2.71828…，所以取3是最好的，如果取不到3就取2。

幂运算复杂度为O(lgn)，所以这个算法复杂度为O(lgn)。

代码如下

class Solution {
public:
    int integerBreak(int n) {
        if(n == 2)
            return 1;
        else if(n == 3)
            return 2;
        else if(n%3 == 0)
            return pow(3, n/3);
        else if(n%3 == 1)
            return 2 * 2 * pow(3, (n - 4) / 3);
        else
            return 2 * pow(3, n/3);
    }
};