Java 树结构实际应用 四（平衡二叉树/AVL树）

平衡二叉树(AVL 树)

1 看一个案例(说明二叉排序树可能的问题)

给你一个数列{1,2,3,4,5,6}，要求创建一颗二叉排序树(BST), 并分析问题所在.

 左边 BST 存在的问题分析:

1) 左子树全部为空，从形式上看，更像一个单链表.

2) 插入速度没有影响

3) 查询速度明显降低(因为需要依次比较), 不能发挥 BST

的优势，因为每次还需要比较左子树，其查询速度比

单链表还慢

4) 解决方案-平衡二叉树(AVL)

 

2 基本介绍

1) 平衡二叉树也叫平衡二叉搜索树（Self-balancing binary search tree）又被称为 AVL 树， 可以保证查询效率较高。

2) 具有以下特点：它是一 棵空树或它的左右两个子树的高度差的绝对值不超过 1，并且左右两个子树都是一棵

平衡二叉树。平衡二叉树的常用实现方法有红黑树、AVL、替罪羊树、Treap、伸展树等。

3) 举例说明, 看看下面哪些 AVL 树, 为什么?

3 应用案例-单旋转(左旋转)

1) 要求: 给你一个数列，创建出对应的平衡二叉树.数列 {4,3,6,5,7,8}

2) 思路分析(示意图)

3)代码实现

// 左旋转
    private void leftRotate() {
        // 创建新的节点，以当前根节点的值
        SNode newNode = new SNode(value);
        // 把新的节点左子树设置成当前节点的左子树
        newNode.left = left;
        // 把新节点的右子树设置成当前节点的右子节点的左子树
        newNode.right = right.left;
        //    把当前节点的值换为右子节点的值
        value = right.value;
        // 把当前节点的右子树换成右子树的右子树
        right = right.right;
        // 把当前节点的左子树设置成新节点
        left = newNode;

    }

4 应用案例-单旋转(右旋转)

1) 要求: 给你一个数列，创建出对应的平衡二叉树.数列 {10,12, 8, 9, 7, 6}

2) 思路分析(示意图)

3)代码实现

// 右旋转
    private void rightRotate() {
        SNode newNode = new SNode(value);
        newNode.right = right;
        newNode.left = left.right;
        value = left.value;
        left = left.left;
        right = newNode;

    }

5 应用案例-双旋转

前面的两个数列，进行单旋转(即一次旋转)就可以将非平衡二叉树转成平衡二叉树,但是在某些情况下，单旋转

不能完成平衡二叉树的转换。比如数列

int[] arr = { 10, 11, 7, 6, 8, 9 }; 运行原来的代码可以看到，并没有转成 AVL 树.

int[] arr = {2,1,6,5,7,3}; // 运行原来的代码可以看到，并没有转成 AVL 树

1) 问题分析

2) 解决思路分析

1. 当符号右旋转的条件时

2. 如果它的左子树的右子树高度大于它的左子树的高度

3. 先对当前这个结点的左节点进行左旋转

4. 在对当前结点进行右旋转的操作即可

3) 代码实现[AVL 树的汇总代码(完整代码)]

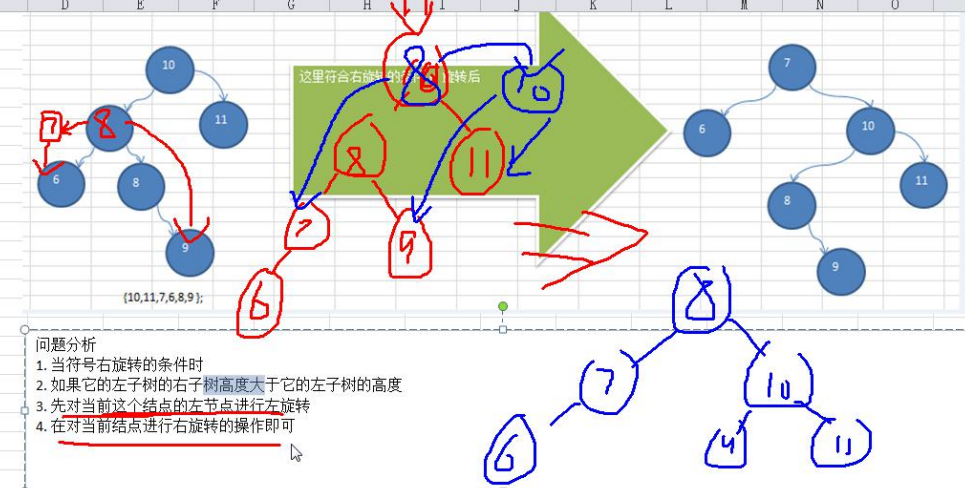
package com.lin.avltree_0316;

import javax.security.auth.kerberos.KerberosKey;

public class AVLTreeDemo {

    public static void main(String[] args) {
//        int[] arr = {4, 3, 6, 5, 7, 8};
//        int[] arr = {10, 12, 8, 9, 7, 6};
        int[] arr = {10, 11, 7, 6, 8, 9};

        AVLTree avlTree = new AVLTree();
        for (int i = 0; i < arr.length; i++) {
            avlTree.add(new SNode(arr[i]));
        }

        avlTree.infixOrder();

        System.out.println("旋转之后：");
        System.out.println("树的高度：" + avlTree.getRoot().height());
        System.out.println("左子树的高度：" + avlTree.getRoot().leftHeight());
        System.out.println("右子树的高度：" + avlTree.getRoot().rightHeight());
        System.out.println("root = " + avlTree.getRoot());
        System.out.println("root.left = " + avlTree.getRoot().left);
        System.out.println("root.left.left = " + avlTree.getRoot().left.left);
    }
}

class AVLTree{
    private SNode root;
    // 查找要删除的节点
    public SNode getRoot() {
        return root;
    }
    public SNode searchDelNode(int value) {
        if(root == null) {
            return null;
        } else {
            return root.searchDelNode(value);
        }
    }
    // 查找要删除节点的父节点
    public SNode searchParent(int value) {
        if(root == null) {
            return null;
        } else {
            return root.searchParent(value);
        }
    }
    /**
     * @param node 传入的节点（当作二叉排序树的根节点）
     * @return 返回的以node为根节点的二叉排序树的最小节点的值
     */
    public int delRightTreeMin(SNode node) {
        SNode target = node;
        //    循环地查找左节点，就会找到最小值
        while(target.left != null) {
            target = target.left;
        }
        delNode(target.value);// !!!!
        return target.value;//   !!!!!
    }

    // 删除节点
    public void delNode(int value) {
        if(root == null) {
            return;
        } else {
            //     找删除节点
            SNode targetNode = searchDelNode(value);
            //     没有找到
            if(targetNode == null) {
                return;
            }
            //    如果发现当前这棵二叉树只有一个节点
            if(root.left == null && root.right == null) {
                root = null;
                return;
            }
            //     去找到targetNode的父节点
            SNode parent = searchParent(value);
            //     如果删除的节点是叶子节点
            if(targetNode.left == null && targetNode.right == null) {
                //    判断targetNode是父节点的左子节点还是右子节点
                if(parent.left != null && parent.left.value == value) {
                    parent.left = null;
                } else if(parent.right != null && parent.right.value == value) {
                    parent.right = null;
                }
            } else if(targetNode.left != null && targetNode.right != null) { //    有左右子节点
                int delRightTreeMin = delRightTreeMin(targetNode.right);
                targetNode.value = delRightTreeMin;
            } else {//    只有一个子节点
                //     要删除的节点只有左节点
                if(targetNode.left !=  null) {
                    if(parent != null) {
                        //     如果targetNode是parent的左子节点
                        if(parent.left.value == value) {
                            parent.left = targetNode.left;
                        } else {
                            parent.right = targetNode.left;
                        }
                    } else {
                        root = targetNode.left;
                    }
                } else {//    要删除的节点有右子节点
                    if(parent != null) {
                        if(parent.left.value == value) {
                            parent.left = targetNode.right;
                        } else {
                            parent.right = targetNode.right;
                        }
                    } else {
                        root = targetNode.right;
                    }
                }
            }

        }
    }
    // 中序遍历
    public void infixOrder() {
        if(root == null) {
            System.out.println("空树！");
        } else {
            root.infixOrder();
        }
    }
    // 添加
    public void add(SNode node) {
        if(root == null) {
            root = node;
        } else {
            root.add(node);
        }
    }
}

class SNode{
    protected int value;
    protected SNode left;
    protected SNode right;

    public SNode(int value) {
        // TODO Auto-generated constructor stub
        this.value = value;
    }
    // 返回左子树的高度
    public int leftHeight() {
        if(left == null) {
            return 0;
        }
        return left.height();
    }
    // 返回右子树的高度
    public int rightHeight() {
        if(right == null) {
            return 0;
        }
        return right.height();
    }
    // 返回当前节点的高度，以该节点为根节点的树的高度
    public int height() {
        return Math.max(left == null ? 0: left.height(), right == null ? 0 : right.height()) + 1;
    }

    // 左旋转
    private void leftRotate() {
        // 创建新的节点，以当前根节点的值
        SNode newNode = new SNode(value);
        // 把新的节点左子树设置成当前节点的左子树
        newNode.left = left;
        // 把新节点的右子树设置成当前节点的右子节点的左子树
        newNode.right = right.left;
        //    把当前节点的值换为右子节点的值
        value = right.value;
        // 把当前节点的右子树换成右子树的右子树
        right = right.right;
        // 把当前节点的左子树设置成新节点
        left = newNode;

    }

    // 右旋转
    private void rightRotate() {
        SNode newNode = new SNode(value);
        newNode.right = right;
        newNode.left = left.right;
        value = left.value;
        left = left.left;
        right = newNode;

    }

    @Override
    public String toString() {
        // TODO Auto-generated method stub
        return "Node = [value = " + value + "]";
    }

    // 添加节点
    public void add(SNode node) {
        if(node == null) {
            return;
        }
        if(node.value < this.value) {
            if(this.left == null) {
                this.left = node;
            } else {
                this.left.add(node);
            }
        } else {
            if(this.right == null) {
                this.right = node;
            } else {
                this.right.add(node);
            }
        }

        // 当添加完后，如果右子树的高度-左子树的高度 > 1， 左旋转
        if( ( rightHeight() - leftHeight() ) > 1 ) {
            // 如果当前节点的右子树的左子树高度大于右子树的高度
            if(right != null && (right.leftHeight() > rightHeight() ) ) {
                right.rightRotate();
                leftRotate();
            } else {
                leftRotate();
            }
            return;//!!!!
        }

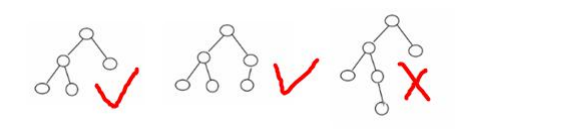
        if ((leftHeight() - rightHeight()) > 1) {
            // 如果当前节点的左子树的右子树高度大于左子树的高度
            if (left != null && (left.rightHeight() > left.leftHeight())) {
                // 先对当前节点的左节点进行左旋转
                left.leftRotate();
                // 再对当前节点进行右旋转
                rightRotate();
            } else {
                rightRotate();
            }
        }
    }
    // 中序遍历
    public void infixOrder() {
        if(this.left != null) {
            this.left.infixOrder();
        }
        System.out.println(this);
        if(this.right != null) {
            this.right.infixOrder();
        }
    }
    // 查找要删除的节点
    public SNode searchDelNode(int value) {
        if(this.value == value) {
            return this;
        } else if(this.value > value) {
            // 如果左子节点为空
            if(this.left == null) {
                return null;
            }
            return this.left.searchDelNode(value);
        } else {
            if(this.right == null) {
                return null;
            }
            return this.right.searchDelNode(value);
        }
    }
    // 查找要删除节点的父节点, 如果没有则返回null
    public SNode searchParent(int value) {
        if(( this.left != null && this.left.value == value)
                || ( this.right != null && this.right.value == value )) {
            return this;
        } else {
             // 如果查找的值小于当前节点的值，并且当前节点的左子节点不为空
            if(value < this.value && this.left != null) {
                return this.left.searchParent(value);
            } else if(value >= this.value && this.right != null) {
                return this.right.searchParent(value);
            } else {
                return null;
            }
        }
    }

}

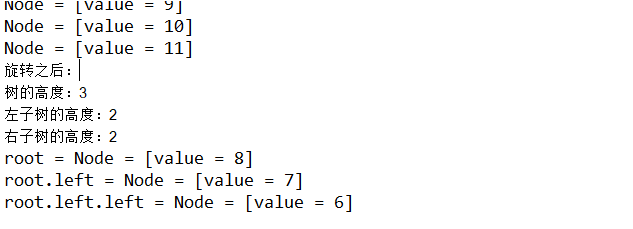
仅供参考，有错误还请指出！

有什么想法，评论区留言，互相指教指教。

觉得不错的可以点一下右边的推荐哟