manacher(马拉车算法)

Manacher(马拉车算法)

---

序言

mannacher 是一种在 O(n)时间内求出最长回文串的算法

我们用暴力求解最长回文串长度的时间复杂度为O(n³)

很明显，这个时间复杂度我们接受不了，这时候，manacher也就是俗称的马拉车算法就出世了

算法描述

先考虑一种在O(n²)的时间复杂度内求解的算法

我们可以从左到右枚举字符串的每一个字符，以当前字符为起点，向左，和向右同事延伸来求解

回文长度，但我们深入分析一下，发现，这个算法明显是有漏洞的，它只能解决字符串长度为

为奇数的回文长度，偶数的字符串无法由它求出回文长度。

比如aba用该算法求出的值为3是正确的,但abba用该算法求出的值却是1，很明显，是错误的，那么我们考虑，

如何去优化该算法，使得奇数和偶数都能解决，我们考虑在字符串的首尾和字符

串间隔中插入一个特殊字符如\(,例如abba,插入后就变为了\)a\(b\)b\(a\)字符串的长

度由n变为了2n+1这样就可以保证字符串的长度为奇数了，证明很简单，2n定为偶数

则2n+1一定为奇数然后便可以通过上述算法求出目前的回文长度了。

但，n² 的算法仍然无法满足我们的需求，我们考虑继续优化，那么如何优化呢？

我们需要引入几个定义

下述定义用未插入特殊字符的字符串进行解释

1：回文中心，即一回文串的中心字符比如abcba这个回文串，从左向右数的第3个字符即c

便为其回文中心我们因为我们对字符串进行了处理，所以便保证了每一串都有其回文中心

2，回文半径，即回文串的最右边界到回文中心的字符个数（包含回文中心）

我们可以发现，每个串的回文半径的长度*2-1便是所求回文串的长度

所以，我们只要求出那个最大的回文半径便可得到最长回文串长度

那么，我们如何求解呢？

manacher算法的本质便是对上面所提的n²的优化

我们看下图，假设我们目前枚举到i，定义r为到目前为止的回文串的最右边界，即目前为止的所

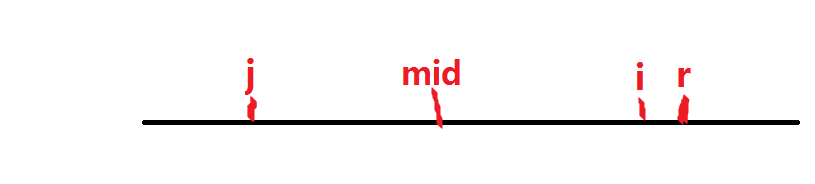
有回文串中，最右的字符下标最大的那个下标；mid则为 r 所在回文串的回文中心

我们对i进行讨论

当i<r时因为i位于以mid为回文中心的回文串中，所以以i为回文中心的字符串有可能被以mid

为回文中心的字符串包含，假设被包含，我们利用回文串的对称性可知，以i关于mid的对称点也就是j点

为回文中心的字符半径等于以i为半径的回文半径

我们直接赋值即可

定义p数组为回文半径长度

那么我们如何判断呢？当r-i的长度要大于p [j] 时，p[j]一定没有超过mid的范围，那么，我们直接对称过去更新p[i]即可

反之，当r-i>r-i 表明p[j]有可能包含mid范围之外的数，我们无法将p[j]赋给p[i]便在范围内将r-i赋给p[i];

本质融合成一句代码便是

p[i]=p[mid*2-i]>mir-i?mir-i:p[mid*2-i];

我们求j的下标利用中点坐标公式求解即可

贴一发代码

#include<iostream>
#include<cstring>
#include<string>
#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn =2e7+10;
char s[maxn];
char ns[maxn];
int p[maxn];
int getle(){
	int len=strlen(s);
	int j=2;
	ns[0]='~';//设置枚举边界，字符串右侧带有换行，所以我们右侧不必放字符了
	ns[1]='$';
	for(int i=0;i<len;i++){
		ns[j++]=s[i];
		ns[j++]='$';
	}
	return j;
}
int manacher(){
	int len=getle();
	int mid=1;
	int mir=1;
	int ans=-1;
	for(int i=1;i<len;i++){
		if(mir>=i){
			p[i]=p[mid*2-i]>mir-i?mir-i:p[mid*2-i];
		}
		else{
			p[i]=1;
		}
		while(ns[i+p[i]]==ns[i-p[i]]){
			p[i]++;
		}
		if(p[i]+i>mir){
			mid=i;
			mir=p[i]+i;
		}
		ans=max(p[i]-1,ans);
	}
	return ans;
}
int main(){
	cin>>s;
	cout<<manacher();
	return 0;
}

完结撒花