伸展树（Splay）学习笔记

二叉排序树能够支持多种动态集合操作，它可以被用来表示有序集合，建立索引或优先队列等。因此，在信息学竞赛中，二叉排序树应用非常广泛。

作用于二叉排序树上的基本操作，其时间复杂度均与树的高度成正比，对于一棵有 \(n\) 个节点的二叉树，这些操作在最有情况下运行时间为 \(O( \log_2 n)\)。

但是，如果二叉树退化成了一条 \(n\) 个节点组成的线性链表，则这些操作在最坏情况下的运行时间为 \(O(n)\)。

有些二叉排序树的变形，其基本操作的性能在最坏情况下依然很好，如平衡树（AVL）等。但是，它们需要额外的空间来存储平衡信息，且实现起来比较复杂。同时，如果访问模式不均匀，平衡树的效率就会受到影响，而伸展树却可以克服这些问题。

伸展树（Splay Tree），是对二叉排序树的一种改进。虽然它并不能保证树一直是“平衡”的，但对于它的一系列操作，可以证明其每一步操作的“平摊时间”复杂度都是 \(O(\log_2 n)\) 。平摊时间是指在一系列最坏情况的操作序列中单次操作的平均时间。所以，从某种意义上来说，伸展树也是一种平衡的二叉排序树。而在各种树形数据结构中，伸展树的空间复杂度（不需要记录用于平衡的冗余信息）和编程复杂度也都是很优秀的。

获得较好平摊效率的一种方法就是使用“自调整”的数据结构，与平衡结构或有明确限制的数据结构相比，自调整的数据结构有一下几个优点：

1. 从平摊角度上，它们忽略常数因子，因此绝对不会差于有明确限制的数据结构，而且它们可以根据具体使用情况进行调整，所以在使用模式不均匀的情况下更加有效；
2. 由于无需存储平衡信息或者其他限制信息，所以所需的存储空间更小；
3. 它们的查找和更新的算法与操作都很简单，易于实现。

当然，自调整的数据结构也有其潜在的缺点：

1. 它们需要更多的局部调整，尤其在查找期间，而那些有明确限制的数据结构仅需要在更新期间进行调整，查找期间则不需要；
2. 一系列查找操作中的某一个可能会耗时较长，这在实时处理的应用程序中可能是一个不足之处。

1. 伸展树的主要操作

伸展树是对二叉排序树的一种改进。与二叉排序树一样，伸展树也具有有序性，即伸展树中的每一个节点 \(x\) 都满足：该节点左子树中的每一个元素都小于 \(x\)，而其右子树中的每一个元素都大于 \(x\)。

但是，与普通二叉排序树不同的是，伸展树可以“自我调整”，这就要依靠伸展树的核心操作 —— \(\text{Splay(x, S)}\)。

1.1 伸展操作

伸展操作 \(\text{Splay(x, S)}\) 是在保持伸展树有序的前提下，通过一系列旋转，将伸展树 \(\text{S}\) 中的元素 \(\text{x}\) 调整至数的根部。在调整的过程中，要分以下三种情况分别处理。

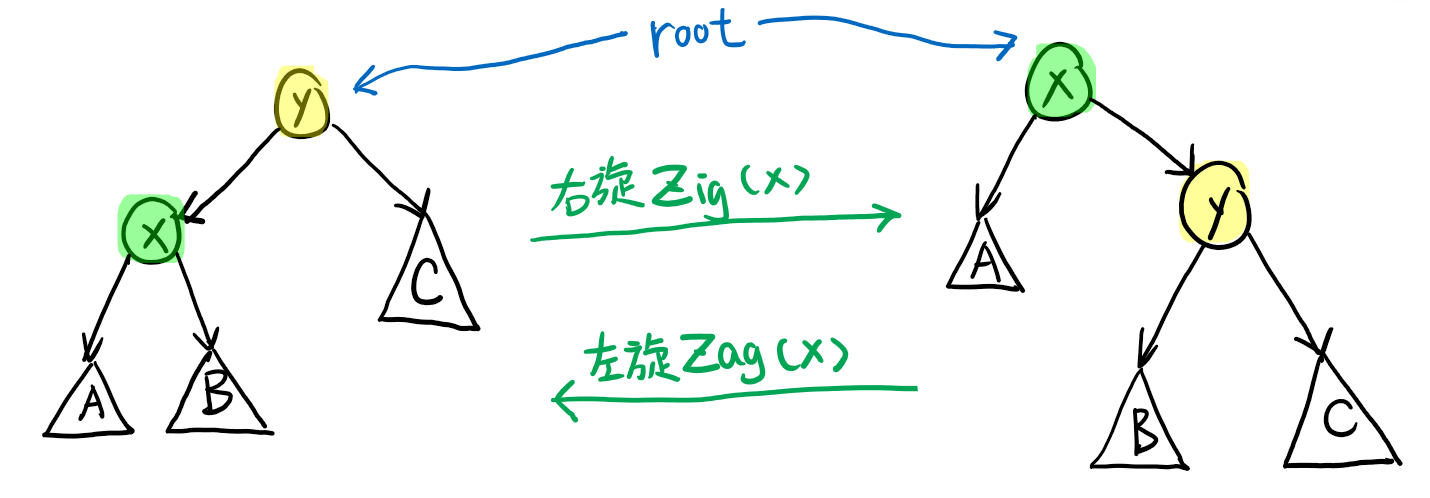
情况一：节点 \(\text{x}\) 的父节点 \(\text{y}\) 是根节点。

此时，

• 若 \(\text{x}\) 是 \(\text{y}\) 的左儿子，则我们进行一次右旋操作 \(\text{Zig(x)}\)；
• 若 \(\text{x}\) 是 \(\text{y}\) 的右儿子，则我们进行一次左旋操作 \(\text{Zag(x)}\)。

经过旋转，使 \(\text{x}\) 成为二叉排序树 \(S\) 的根节点，且依然满足二叉排序树的性质。

\(\text{Zig}\) 操作和 \(\text{Zag}\) 操作如图所示：

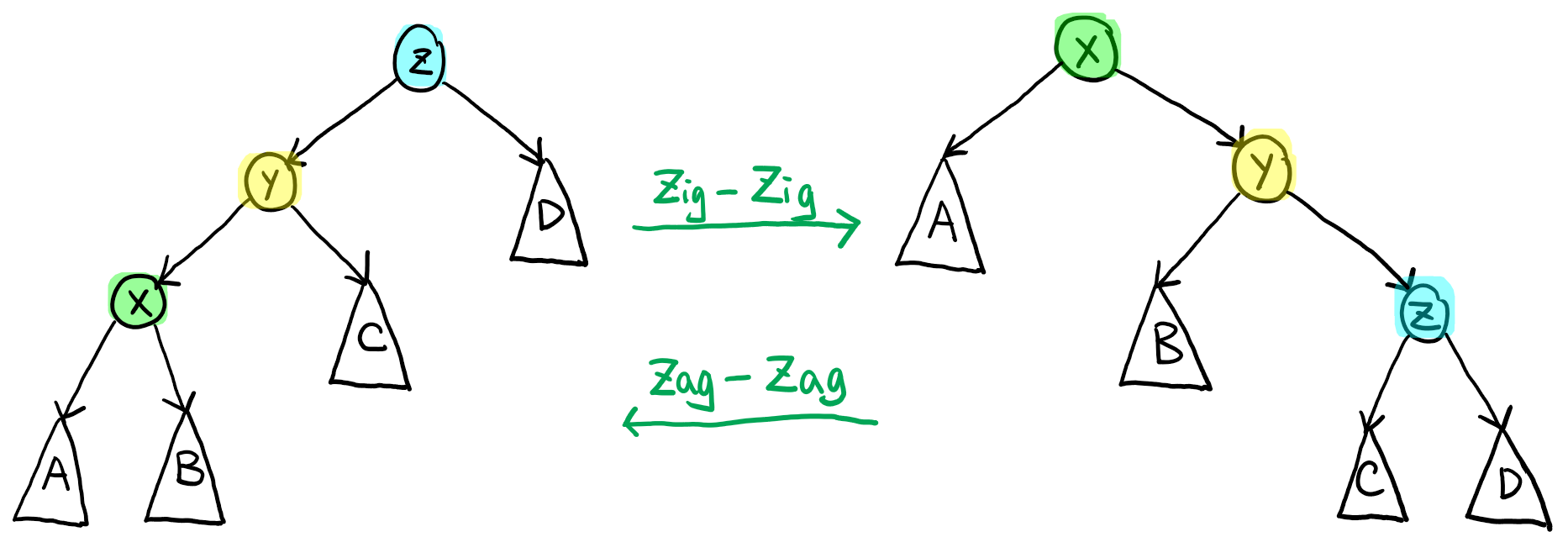
情况二：节点 \(\text{x}\) 的父节点 \(\text{y}\) 不是根节点，且 \(\text{x}\) 和 \(\text{y}\) 同为各自父节点的左儿子，或同为各自父节点的右儿子。

此时，我们设 \(\text{z}\) 为 \(\text{y}\) 的父节点，

• 若 \(\text{x}\) 和 \(\text{y}\) 同时是各自父节点的左儿子，则进行一次 \(\text{Zig-Zig}\) 操作；
• 若 \(\text{x}\) 和 \(\text{y}\) 同时是各自父节点的右儿子，则进行一次 \(\text{Zag-Zag}\) 操作。

如图所示：

情况三：节点 \(\text{x}\) 的父节点 \(\text{y}\) 不是根节点，且 \(\text{x}\) 和 \(\text{y}\) 中的一个是其父节点的左儿子，另一个是其父节点的右儿子。

此时，我们设 \(\text{z}\) 为 \(\text{y}\) 的父节点，

• 若 \(\text{x}\) 是 \(\text{y}\) 的左儿子，\(\text{y}\) 是 \(\text{z}\) 的右儿子，则进行一次 \(\text{Zig-Zag}\) 操作；
• 若 \(\text{x}\) 是 \(\text{y}\) 的右儿子，\(\text{y}\) 是 \(\text{z}\) 的左二子，则进行一次 \(\text{Zag-Zig}\) 操作。

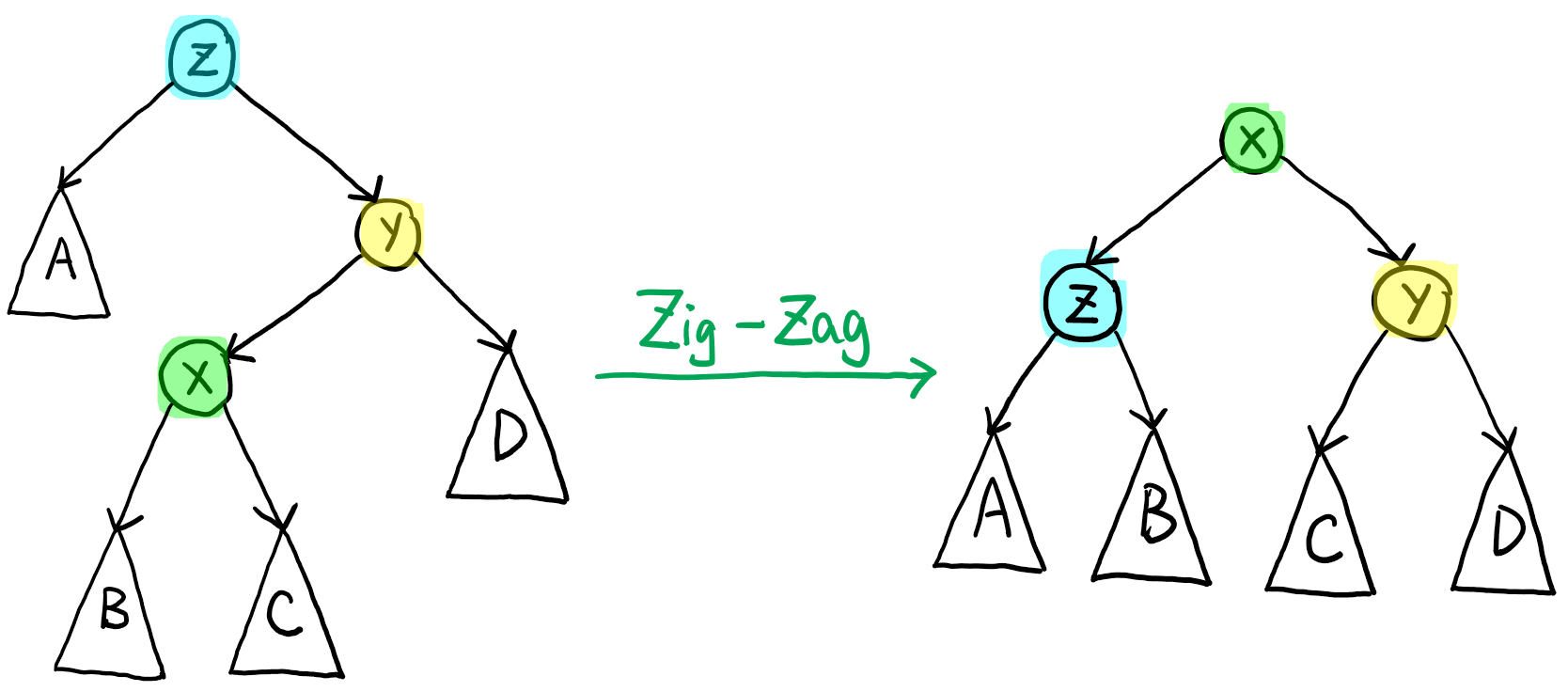
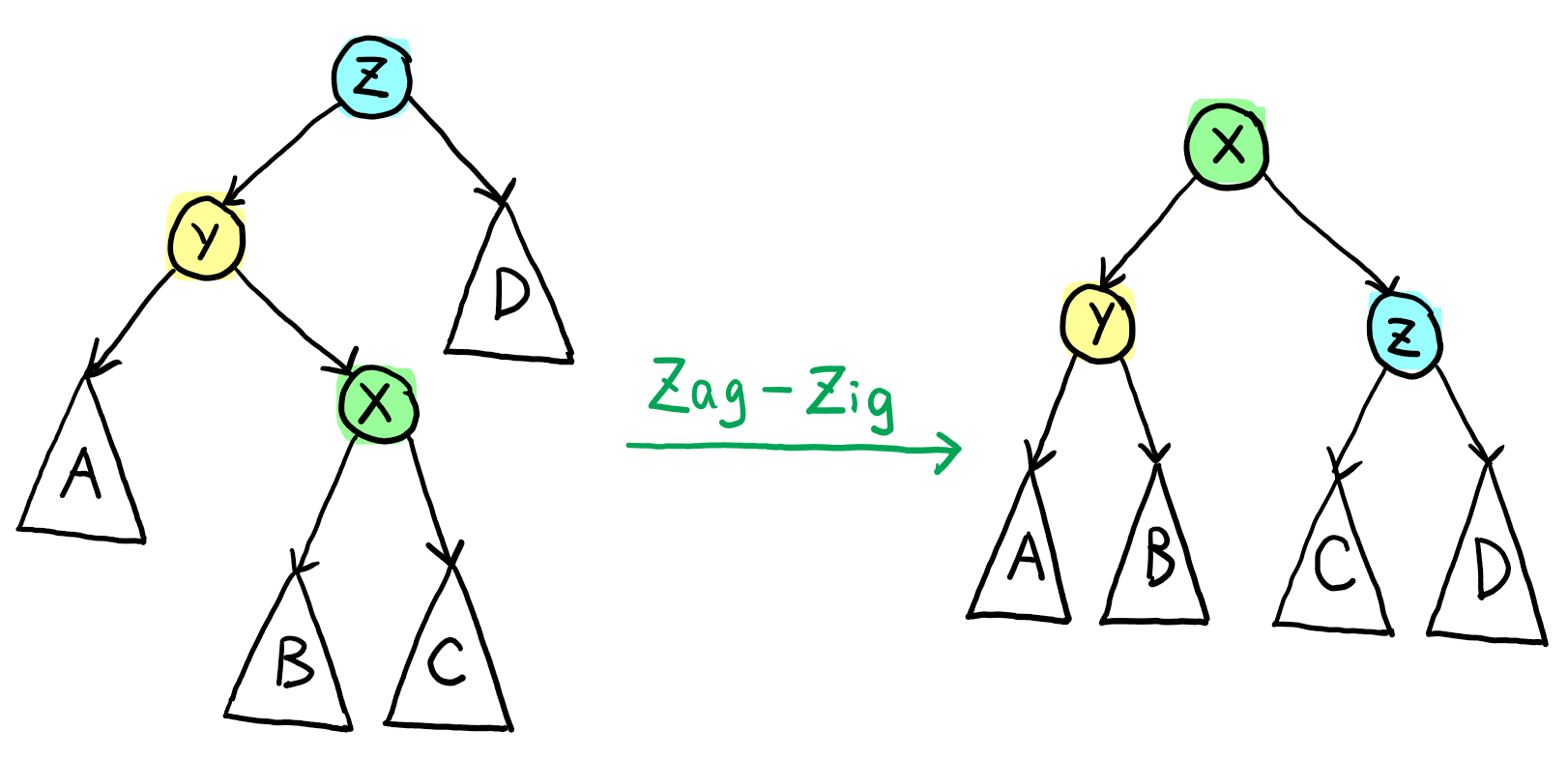
下面举一个例子来体会上面的伸展操作。

如下图所示，最左边的一个单链先执行 \(\text{Splay(1, S)}\)，我们将元素 \(1\) 调整到了伸展树的根部。

执行几次 \(\text{Splay(1, S)}\) 的效果

然后再执行 \(\text{Splay(2, S)}\)，将元素 \(2\) 调整到伸展树 \(\text{S}\) 的根部。如下图所示：

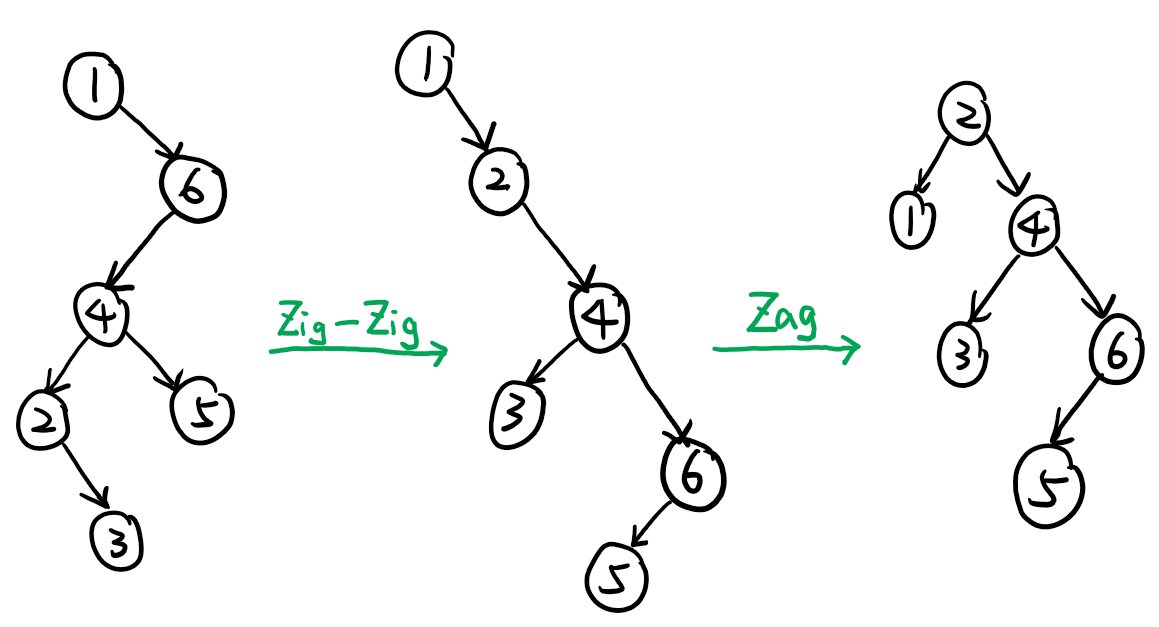
执行几次 \(\text{Splay(2, S)}\) 的效果

1.2 伸展树的基本操作

利用伸展树 Splay ，我们可以在伸展树 \(S\) 上进行如下几种基本操作。

（1） \(\text{Find(x, S)}\)：判断元素 \(\text{x}\) 是否在伸展树 \(\text{S}\) 表示的有序集中。

首先，与在二叉排序树中进行查找操作操作一样，在伸展树中查找元素 \(\text{x}\)。如果 \(\text{x}\) 在树中，则再执行 \(\text{Splay(x, S)}\) 调整伸展树。

（2） \(\text{Insert(x, S)}\)：将元素 \(\text{x}\) 插入到伸展树 \(S\) 表示的有序集中。

首先，与在二叉排序树中进行插入操作一样，将 \(\text{x}\) 插入到伸展树 \(\text{S}\) 中的相应位置，再执行 \(\text{Splay(x, S)}\) 调整伸展树。

（3） \(\text{Join(S1, S2)}\)：将两棵伸展树 \(\text{S1}\) 与 \(\text{S2}\) 合并成为一棵伸展树。其中，\(S1\) 的所有元素都小于 \(S2\) 的所有元素。

首先，找到伸展树 \(S1\) 中最大的一个元素 \(\text{x}\)，再通过 \(\text{Splay(x, S1)}\) 将 \(\text{x}\) 调整到伸展树 \(S1\) 的根部。然后将 \(S2\) 作为 \(\text{x}\) 节点的右子树插入，这样就得到了新的伸展树 \(S\)，如图所示：

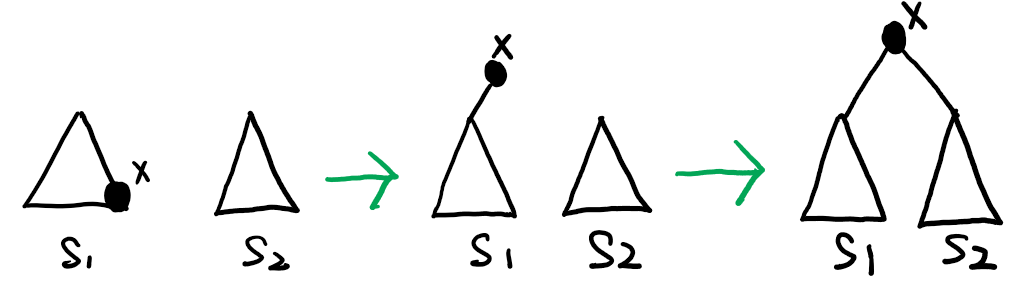
\(\text{Join(S1, S2)}\) 的两个步骤

（4）\(\text{Delete(x, S)}\)：将元素 \(x\) 从伸展树 \(S\) 所表示的有序集中删除。

首先，执行 \(\text{Find(x, S)}\) 将 \(\text{x}\) 调整为根节点，然后再对左右子树执行 \(\text{Join(S1, S2)}\) 操作即可。

（5）\(\text{Split(x, S)}\)：以 \(x\) 为界，将伸展树 \(S\) 分离为两棵伸展树 \(S1\) 和 \(S2\)，其中，\(S1\) 的所有元素都小于 \(x\)，\(S2\) 的所有元素都大于 \(x\)。

首先，执行 \(\text{Find(x, S)}\) 将 \(\text{x}\) 调整为根节点，则 \(\text{x}\) 的左子树就是 \(\text{S1}\)，右子树就是 \(\text{S2}\)。如图所示：

除了上述介绍的 \(5\) 种基本操作外，伸展树还支持求最大值、最小值、求前趋、求后继等多种操作，这些操作也都是建立在伸展树操作 \(\text{Splay}\) 的基础之上的。

2. 伸展树的算法实现

注：这里的代码并不是最简单的代码，而是基于上述思想实现的代码，更方便我们结合之前分析的内容来理解。

下面给出伸展树的各种操作的算法实现，它们都是基于如下伸展树的类型定义：

int lson[maxn], // 左儿子编号
    rson[maxn], // 右儿子编号
    p[maxn],    // 父节点编号
    val[maxn],  // 节点权值
    sz;         // 编号范围 [1, sz]

struct Splay {
    int rt; // 根节点编号
    void zag(int x);    // 左旋
    void zig(int x);    // 右旋
    void splay(int x);  // 伸展操作：将x移到根节点
    int func_find(int v);   // 查找是否存在值为v的节点
    void func_insert(int v);    // 插入
    void func_delete(int v);    // 删除
    int get_max();  // 求最大值
    int get_min();  // 求最小值
    int get_pre(int v); // 求前趋
    int get_suc(int v); // 求后继
    int join(int rt1, int rt2); // 合并
} tree;

1. 左旋操作

void Splay::zag(int x) {
    int y = p[x], z = p[y], a = lson[x];
    lson[x] = y; p[y] = x;
    rson[y] = a; p[a] = y;
    p[x] = z;
    if (z) {
        if (lson[z] == y) lson[z] = x;
        else rson[z] = x;
    }
}

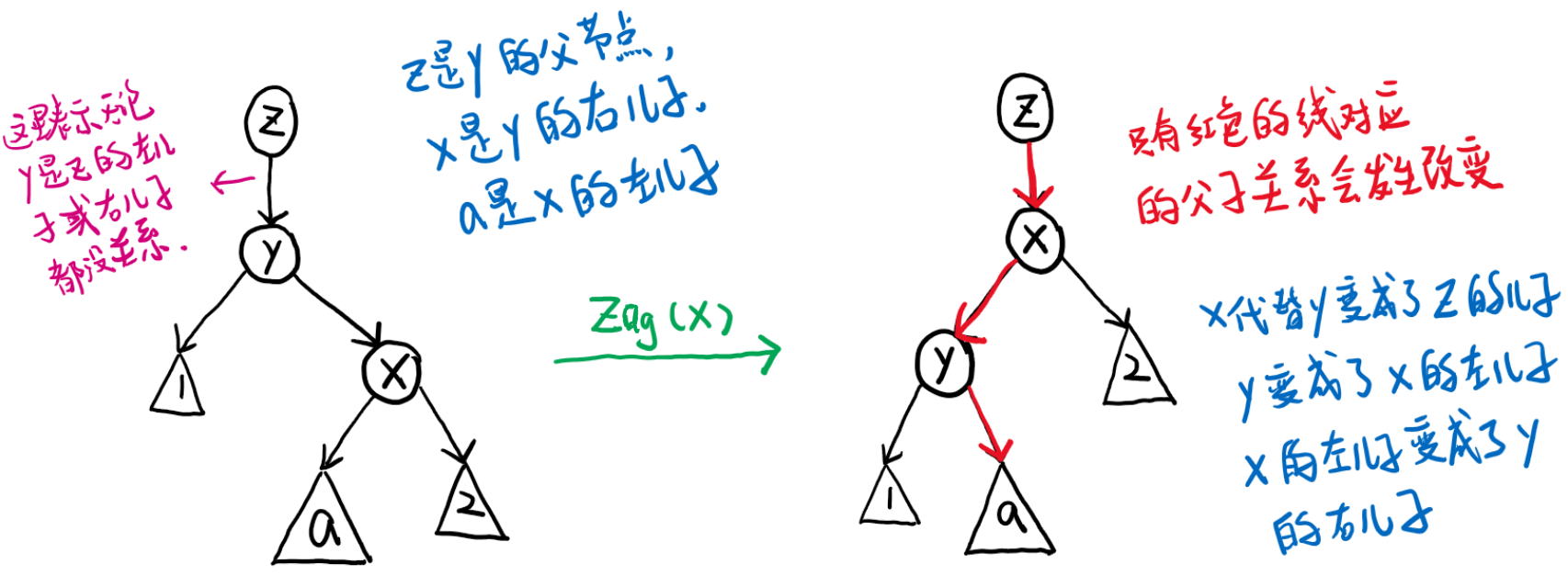
Zag(x)操作

2. 右旋操作

void Splay::zig(int x) {
    int y = p[x], z = p[y], a = rson[x];
    rson[x] = y; p[y] = x;
    lson[y] = a; p[a] = y;
    p[x] = z;
    if (z) {
        if (lson[z] == y) lson[z] = x;
        else rson[z] = x;
    }
}

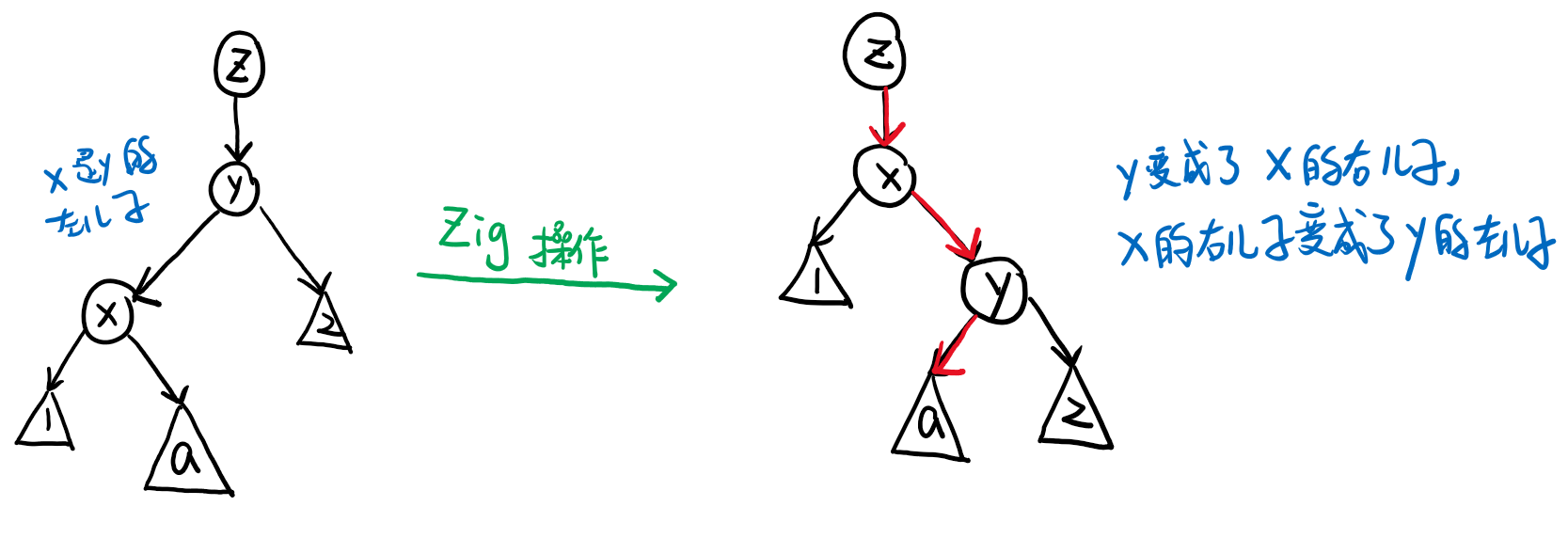
Zig(x)操作

3. 伸展操作

void Splay::splay(int x) {
    while (p[x]) {
        int y = p[x], z = p[y];
        if (!z) {
            if (x == lson[y]) zig(x);
            else zag(x);
        }
        else if (lson[y] == x) {
            if (lson[z] == y) { // zig-zig
                zig(y);
                zig(x);
            }
            else {  // zig-zag
                zig(x);
                zag(x);
            }
        }
        else {  // rson[y] == x
            if (lson[z] == y) { // zag-zig
                zag(x);
                zig(x);
            }
            else {  // zag-zag
                zag(y);
                zag(x);
            }
        }
    }
    rt = x;
}

4. 查找

int Splay::func_find(int v) {
    int x = rt;
    while (x) {
        if (val[x] == v) {
            rt = x;
            splay(x);
            return x;
        }
        else if (v < val[x]) x = lson[x];
        else x = rson[x];
    }
    return 0;   // 返回0说明没找到
}

5. 插入

void Splay::func_insert(int v) {
    val[++sz] = v;
    if (rt == 0) {
        rt = sz;
        return;
    }
    int x = rt;
    while (true) {
        if (v < val[x]) {
            if (lson[x]) x = lson[x];
            else {
                lson[x] = sz;
                p[sz] = x;
                break;
            }
        }
        else {
            if (rson[x]) x = rson[x];
            else {
                rson[x] = sz;
                p[sz] = x;
                break;
            }
        }
    }
    splay(rt = sz);
}

6. 删除（会用到下面定义的join操作）

void Splay::func_delete(int v) {
    int x = func_find(v);
    if (!x) return;
    int ls = lson[x], rs = rson[x];
    lson[x] = rson[x] = 0;
    p[ls] = p[rs] = 0;
    rt = join(ls, rs);
}

7. 求最大值

int Splay::get_max() {
    if (!rt) return 0;
    int x = rt;
    while (rson[x]) x = rson[x];
    splay(rt = x);
    return x;
}

8. 求最小值

int Splay::get_min() {
    if (!rt) return 0;
    int x = rt;
    while (lson[x]) x = lson[x];
    splay(rt = x);
    return x;
}

9. 求前趋

int Splay::get_pre(int v) {
    if (!rt) return 0;
    int x = rt, ans = 0;
    while (true) {
        if (val[x] <= v) {
            if (!ans || val[ans] < val[x]) ans = x;
            if (rson[x]) x = rson[x];
            else break;
        }
        else {
            if (lson[x]) x = lson[x];
            else break;
        }
    }
    if (ans) splay(rt = ans);
    return ans;
}

10. 求后继

int Splay::get_suc(int v) {
    if (!rt) return 0;
    int x = rt, ans = 0;
    while (true) {
        if (val[x] >= v) {
            if (!ans || val[ans] > val[x]) ans = x;
            if (lson[x]) x = lson[x];
            else break;
        }
        else {
            if (rson[x]) x = rson[x];
            else break;
        }
    }
    if (ans) splay(rt = ans);
    return ans;
}

11. 合并

int Splay::join(int rt1, int rt2) {
    if (!rt1) return rt2;
    if (!rt2) return rt1;
    Splay tree1;
    tree1.rt = rt1;
    rt1 = tree1.get_max();
    assert(rson[rt1] == 0);
    rson[rt1] = rt2;
    p[rt2] = rt1;
    return rt1;
}

示例代码（对应题目：《怪物仓库管理员（二）》）：

#include <bits/stdc++.h>
using namespace std;
const int maxn = 500050;
int lson[maxn], // 左儿子编号
    rson[maxn], // 右儿子编号
    p[maxn],    // 父节点编号
    val[maxn],  // 节点权值
    sz;         // 编号范围 [1, sz]

struct Splay {
    int rt; // 根节点编号
    void zag(int x);    // 左旋
    void zig(int x);    // 右旋
    void splay(int x);  // 伸展操作：将x移到根节点
    int func_find(int v);   // 查找是否存在值为v的节点
    void func_insert(int v);    // 插入
    void func_delete(int v);    // 删除
    int get_max();  // 求最大值
    int get_min();  // 求最小值
    int get_pre(int v); // 求前趋
    int get_suc(int v); // 求后继
    int join(int rt1, int rt2); // 合并
} tree;

/**
    zag(int x) 左旋
*/
void Splay::zag(int x) {
    int y = p[x], z = p[y], a = lson[x];
    lson[x] = y; p[y] = x;
    rson[y] = a; p[a] = y;
    p[x] = z;
    if (z) {
        if (lson[z] == y) lson[z] = x;
        else rson[z] = x;
    }
}

/**
    zig(int x) 右旋
*/
void Splay::zig(int x) {
    int y = p[x], z = p[y], a = rson[x];
    rson[x] = y; p[y] = x;
    lson[y] = a; p[a] = y;
    p[x] = z;
    if (z) {
        if (lson[z] == y) lson[z] = x;
        else rson[z] = x;
    }
}

/**
    splay(int x) 伸展操作
*/
void Splay::splay(int x) {
    while (p[x]) {
        int y = p[x], z = p[y];
        if (!z) {
            if (x == lson[y]) zig(x);
            else zag(x);
        }
        else if (lson[y] == x) {
            if (lson[z] == y) { // zig-zig
                zig(y);
                zig(x);
            }
            else {  // zig-zag
                zig(x);
                zag(x);
            }
        }
        else {  // rson[y] == x
            if (lson[z] == y) { // zag-zig
                zag(x);
                zig(x);
            }
            else {  // zag-zag
                zag(y);
                zag(x);
            }
        }
    }
    rt = x;
}

int Splay::func_find(int v) {
    int x = rt;
    while (x) {
        if (val[x] == v) {
            rt = x;
            splay(x);
            return x;
        }
        else if (v < val[x]) x = lson[x];
        else x = rson[x];
    }
    return 0;   // 返回0说明没找到
}

void Splay::func_insert(int v) {
    val[++sz] = v;
    if (rt == 0) {
        rt = sz;
        return;
    }
    int x = rt;
    while (true) {
        if (v < val[x]) {
            if (lson[x]) x = lson[x];
            else {
                lson[x] = sz;
                p[sz] = x;
                break;
            }
        }
        else {
            if (rson[x]) x = rson[x];
            else {
                rson[x] = sz;
                p[sz] = x;
                break;
            }
        }
    }
    splay(rt = sz);
}

void Splay::func_delete(int v) {
    int x = func_find(v);
    if (!x) return;
    int ls = lson[x], rs = rson[x];
    lson[x] = rson[x] = 0;
    p[ls] = p[rs] = 0;
    rt = join(ls, rs);
}

int Splay::get_max() {
    if (!rt) return 0;
    int x = rt;
    while (rson[x]) x = rson[x];
    splay(rt = x);
    return x;
}

int Splay::get_min() {
    if (!rt) return 0;
    int x = rt;
    while (lson[x]) x = lson[x];
    splay(rt = x);
    return x;
}

int Splay::get_pre(int v) {
    if (!rt) return 0;
    int x = rt, ans = 0;
    while (true) {
        if (val[x] <= v) {
            if (!ans || val[ans] < val[x]) ans = x;
            if (rson[x]) x = rson[x];
            else break;
        }
        else {
            if (lson[x]) x = lson[x];
            else break;
        }
    }
    if (ans) splay(rt = ans);
    return ans;
}

int Splay::get_suc(int v) {
    if (!rt) return 0;
    int x = rt, ans = 0;
    while (true) {
        if (val[x] >= v) {
            if (!ans || val[ans] > val[x]) ans = x;
            if (lson[x]) x = lson[x];
            else break;
        }
        else {
            if (rson[x]) x = rson[x];
            else break;
        }
    }
    if (ans) splay(rt = ans);
    return ans;
}

int Splay::join(int rt1, int rt2) {
    if (!rt1) return rt2;
    if (!rt2) return rt1;
    Splay tree1;
    tree1.rt = rt1;
    rt1 = tree1.get_max();
    assert(rson[rt1] == 0);
    rson[rt1] = rt2;
    p[rt2] = rt1;
    return rt1;
}

int n, op, x;

int main() {
    cin >> n;
    while (n --) {
        cin >> op;
        if (op != 3 && op != 4) cin >> x;
        if (op == 1) tree.func_insert(x);
        else if (op == 2) tree.func_delete(x);
        else if (op == 3) cout << val[tree.get_min()] << endl;
        else if (op == 4) cout << val[tree.get_max()] << endl;
        else if (op == 5) cout << val[tree.get_pre(x)] << endl;
        else cout << val[tree.get_suc(x)] << endl;
    }
    return 0;
}