c语言：分治算法之大数相乘

我们把整数A由规模n分为n1和n2，把整数B由规模m分为m1和m2，如下图：

则A分为n1位的A1和n2位的A1，B分为m1位的B1和m2位的B2，如下式所示：

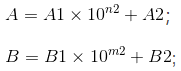
以此类推，我们可以把A1、A2、B1、B2继续划分，直至最小单位。（这里在编程时需要用递归来实现）

上面讲的很清楚了，那么A和B的相乘就可以表示为：

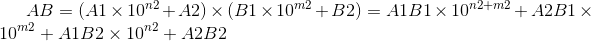
#include <stdio.h>
#include <malloc.h>
#include <stdlib.h>
#include <string.h>

char *result = '\0';
int  pr = 1;

void getFill(char *a,char *b,int ia,int ja,int ib,int jb,int tbool,int move){
    int  r,m,n,s,j,t;
    char *stack;
    // get(a,b,0,0,0,0,1,2)
    m = a[ia] - 48; // m=1
    if( tbool ){// 直接从结果数组的标志位填入,这里用了堆栈思想    这部分实现A1xB1
        r = (jb - ib > ja - ia) ? (jb - ib) : (ja - ia); // r=0
        stack = (char *)malloc(r + 4);  // 因为执行了getFill方法，此时ia=ja,说明两个数必定其中一个是个位数，而jb-ib的值+1即另一个数的位数
        for(r = j = 0,s = jb; s >= ib; r ++,s --){  // r=j=s=0;0>=0;r++,s++   r=1,s=-1
            n = b[s] - 48;  // n=4
            stack[r] = (m * n + j) % 10; //stack[0]=(1x4+0)%10=4  通过模10来获取result[1]位置上的数
            j = (m * n + j) / 10;  // j=(1x4+0)/10 = 0  通过整除来获取result[1]位置上的数，如果j=0,则只需要填写result[1]位置的数；如果j不等于0，则将j放在
        }　　　　　　　　　　　　　　　//　　　　　　　　　　　　result[1]位置，前面取模获取的值放在result[2]所在的位置
        if( j ){  // 如果j 不等于0，如j=1,stack[1]=1,则将stack[1]赋值给result[1],将stack[0]赋值个result[2].由于先有stack[0],再有stack[1],而使用时先用
            stack[r] = j;  // stack[1]=1       stack[1]再用stack[0],即先进后出，所以说使用了栈的思想。
            r ++;  // r=2
        }
        // r=1
        for(r --; r >= 0; r --,pr ++)  // r=0;0>=0; pr=2
            result[pr] = stack[r];  //result[1]=stack[0]=4
        free(stack);
        // move=2 pr=2  由于A1xB1之后后面还要加00，故将result[1]后面的两个字节空间赋值为\0.字符串是以\0作为结束标志的，在内存中，比如字符串“abc”,实际上是4个字节的空间abc\0
        for(move = move + pr; pr < move; pr ++) // move=4;2<4;pr++   pr=3  move=4;3<4;pr++   pr=4
            result[pr] = '\0';                  // result[2]='\0'    result[3]='\0'
    }
    else{ //与结果的某几位相加,这里不改变标志位 pr 的值     //这部分实现A2xB1，A1xB2,A2xB2
        r = pr - move - 1;
        for(s = jb,j = 0; s >= ib; r --,s --){
            n = b[s] - 48;
            t = m * n + j + result[r];
            result[r] = t % 10;
            j = t / 10;
        }
        for( ; j ; r -- ){
            t = j + result[r];
            result[r] = t % 10;
            j = t / 10;
        }
    }
}

int  get(char *a,char *b,int ia,int ja,int ib,int jb,int t,int move){
    int m,n,s,j;

    if(ia == ja){
        getFill(a,b,ia,ja,ib,jb,t,move);
        return 1;
    }
    else if(ib == jb){
        getFill(b,a,ib,jb,ia,ja,t,move);
        return 1;
    }
    else{ // 12x45   get（a,b,0,1,0,1,1,0）
        m = (ja + ia) / 2; //     m=0
        n = (jb + ib) / 2; //     m=0
        s = ja - m;           //     s=1
        j = jb - n;           //       j=1
        get(a,b,ia,m,ib,n,t,s + j + move); //     get(a,b,0,0,0,0,1,2)
        get(a,b,ia,m,n + 1,jb,0,s + move); //      get(a,b,0,0,1,1,0,1)
        get(a,b,m + 1,ja,ib,n,0,j + move); //      get(a,b,1,1,0,0,0,1)
        get(a,b,m + 1,ja,n + 1,jb,0,0 + move); // get(a,b,1,1,1,1,0,0)
    }
    return 0;
}

int  main(){
    char *a,*b;
    int  n,flag;

    a = (char *)malloc(1000);  // 分配所需的内存空间 1000字节
    b = (char *)malloc(1000);
    printf("The program will computer a*b\n");
    printf("Enter a b:");
    scanf("%s %s",a,b);
    result = (char *)malloc(strlen(a) + strlen(b) + 2);
    flag = pr = 1;
    result[0] = '\0';
    if(a[0] == '-' && b[0] == '-')
        get(a,b,1,strlen(a)-1,1,strlen(b)-1,1,0);
    if(a[0] == '-' && b[0] != '-'){
        flag = 0;
        get(a,b,1,strlen(a)-1,0,strlen(b)-1,1,0);
    }
    if(a[0] != '-' && b[0] == '-'){
        flag = 0;
        get(a,b,0,strlen(a)-1,1,strlen(b)-1,1,0);
    }
    if(a[0] != '-' && b[0] != '-')
        get(a,b,0,strlen(a)-1,0,strlen(b)-1,1,0); // get（a,b,0,1,0,1,1,0）
    if(!flag)
        printf("-");
    if( result[0] )
        printf("%d",result[0]);
    for(n = 1; n < pr ; n ++)
        printf("%d",result[n]);
    printf("\n");
    free(a);
    free(b);
    free(result);
    system("pause");
    return 0;
}

void getFill(char *a,char *b,int ia,int ja,int ib,int jb,int tbool,int move){
    int  r,m,n,s,j,t;
    char *stack;
    // get(a,b,0,0,1,1,0,1)   计算A1xB2
    m = a[ia] - 48; // m=1    m为A1的值
    if( tbool ){// 直接从结果数组的标志位填入,这里用了堆栈思想
        r = (jb - ib > ja - ia) ? (jb - ib) : (ja - ia);
        stack = (char *)malloc(r + 4);
        for(r = j = 0,s = jb; s >= ib; r ++,s --){
            n = b[s] - 48;  // n=4
            stack[r] = (m * n + j) % 10;
            j = (m * n + j) / 10;
        }
        if( j ){
            stack[r] = j;
            r ++;
        }
        for(r --; r >= 0; r --,pr ++)
            result[pr] = stack[r];
        free(stack);

        for(move = move + pr; pr < move; pr ++)
            result[pr] = '\0';
    }
    else{ //与结果的某几位相加,这里不改变标志位 pr 的值
        r = pr - move - 1;  // pr=4 move=1  r=4-1-1=2
        for(s = jb,j = 0; s >= ib; r --,s --){ // s=jb=1,j=0;1>=1;r--,s--
            n = b[s] - 48;   // n=5   n为B2的值
            t = m * n + j + result[r];  // t=1*5+0+result[2]=5+0=5
            result[r] = t % 10;  // result[2]=5   将两个数相乘的结果模10得到result[2]上的值，
            j = t / 10;    // j=0   将两个数相乘的结果整除10得到是否需要进一位，
        }
        // r=1,s=0
        for( ; j ; r -- ){
            t = j + result[r];
            result[r] = t % 10;
            j = t / 10;
        }
    }
}

void getFill(char *a,char *b,int ia,int ja,int ib,int jb,int tbool,int move){
    int  r,m,n,s,j,t;
    char *stack;
    // get(a,b,1,1,0,0,0,1)  计算A2xB1
    m = a[ia] - 48; // m=2   m为A2的值
    if( tbool ){// 直接从结果数组的标志位填入,这里用了堆栈思想
        r = (jb - ib > ja - ia) ? (jb - ib) : (ja - ia);
        stack = (char *)malloc(r + 4);
        for(r = j = 0,s = jb; s >= ib; r ++,s --){
            n = b[s] - 48;
            stack[r] = (m * n + j) % 10;
            j = (m * n + j) / 10;
        }
        if( j ){
            stack[r] = j;
            r ++;
        }
        // r=1
        for(r --; r >= 0; r --,pr ++)
            result[pr] = stack[r];
        free(stack);
        for(move = move + pr; pr < move; pr ++)
            result[pr] = '\0';
    }
    else{ //与结果的某几位相加,这里不改变标志位 pr 的值
        r = pr - move - 1;  // pr=4 move=1  r=4-1-1=2
        for(s = jb,j = 0; s >= ib; r --,s --){ // s=jb=0,j=0;0>=0;r--,s--
            n = b[s] - 48;   // n=4   n为B1的值
            t = m * n + j + result[r];  // t=2*4+0+result[2]=8+5=13   两个数相乘的结果加上前面A1xB2的结果
            result[r] = t % 10;  // result[2]=3    将两个数相乘的结果加上前面A1xB2的结果模10得到最后result[2]的值
            j = t / 10;    // j=1  r=1 s=-1   整除10看是否需要进一位，如果需要进一位，则将j与原来result[1]相加，result[1]再对10取模，即可确定result[1]的值
        }
        // r=1,s=-1
        for( ; j ; r -- ){
            t = j + result[r];  // t=1+4=5
            result[r] = t % 10;  // result[1]=5
            j = t / 10;  // j=0 r=0
        }
    }
}

void getFill(char *a,char *b,int ia,int ja,int ib,int jb,int tbool,int move){
    int  r,m,n,s,j,t;
    char *stack;
    // get(a,b,1,1,1,1,0,0)   计算A2xB2
    m = a[ia] - 48; // m=2   m为A2的值
    if( tbool ){// 直接从结果数组的标志位填入,这里用了堆栈思想
        r = (jb - ib > ja - ia) ? (jb - ib) : (ja - ia);
        stack = (char *)malloc(r + 4);
        for(r = j = 0,s = jb; s >= ib; r ++,s --){
            n = b[s] - 48;
            stack[r] = (m * n + j) % 10;
            j = (m * n + j) / 10;
        }
        if( j ){
            stack[r] = j;
            r ++;
        }
        for(r --; r >= 0; r --,pr ++)
            result[pr] = stack[r];
        free(stack);

        for(move = move + pr; pr < move; pr ++)
            result[pr] = '\0';
    }
    else{ //与结果的某几位相加,这里不改变标志位 pr 的值
        r = pr - move - 1;  // pr=4 move=0  r=4-0-1=3
        for(s = jb,j = 0; s >= ib; r --,s --){ // s=jb=1,j=0;1>=1;r--,s--
            n = b[s] - 48;   // n=5    n为B2的值
            t = m * n + j + result[r];  // t=2*5+0+result[3]=10+0=10  将两个数相乘再加上原来这个位置的值
            result[r] = t % 10;  // result[3]=0   模10得到这个位置上的值，
            j = t / 10;    // j=1  r=2 s=0        整除10看是否需要进一位，如果需要进一位，则j+result[2]得到最终的值
        }
        // r=2,s=-1
        for( ; j ; r -- ){
            t = j + result[r];  // t=1+result[2]=1+3=4
            result[r] = t % 10;  // result[2]=4
            j = t / 10;  // j=0 r=1
        }
    }
}

总结：

get(a,b,0,0,0,0,1,2) 1x4 00 result[1]=4（初值）
get(a,b,0,0,1,1,0,1) 1x5  0  result[2]=5（初值）
get(a,b,1,1,0,0,0,1) 2x4  0  result[2]=3（初值）  result[1]=5  （终值）
get(a,b,1,1,1,1,0,0) 2x5      result[3]=0（终值） result[2]=4（终值）