[LeetCode]69. x 的平方根(数学，二分)

题目

https://leetcode-cn.com/problems/sqrtx

题解

方法一：牛顿迭代法

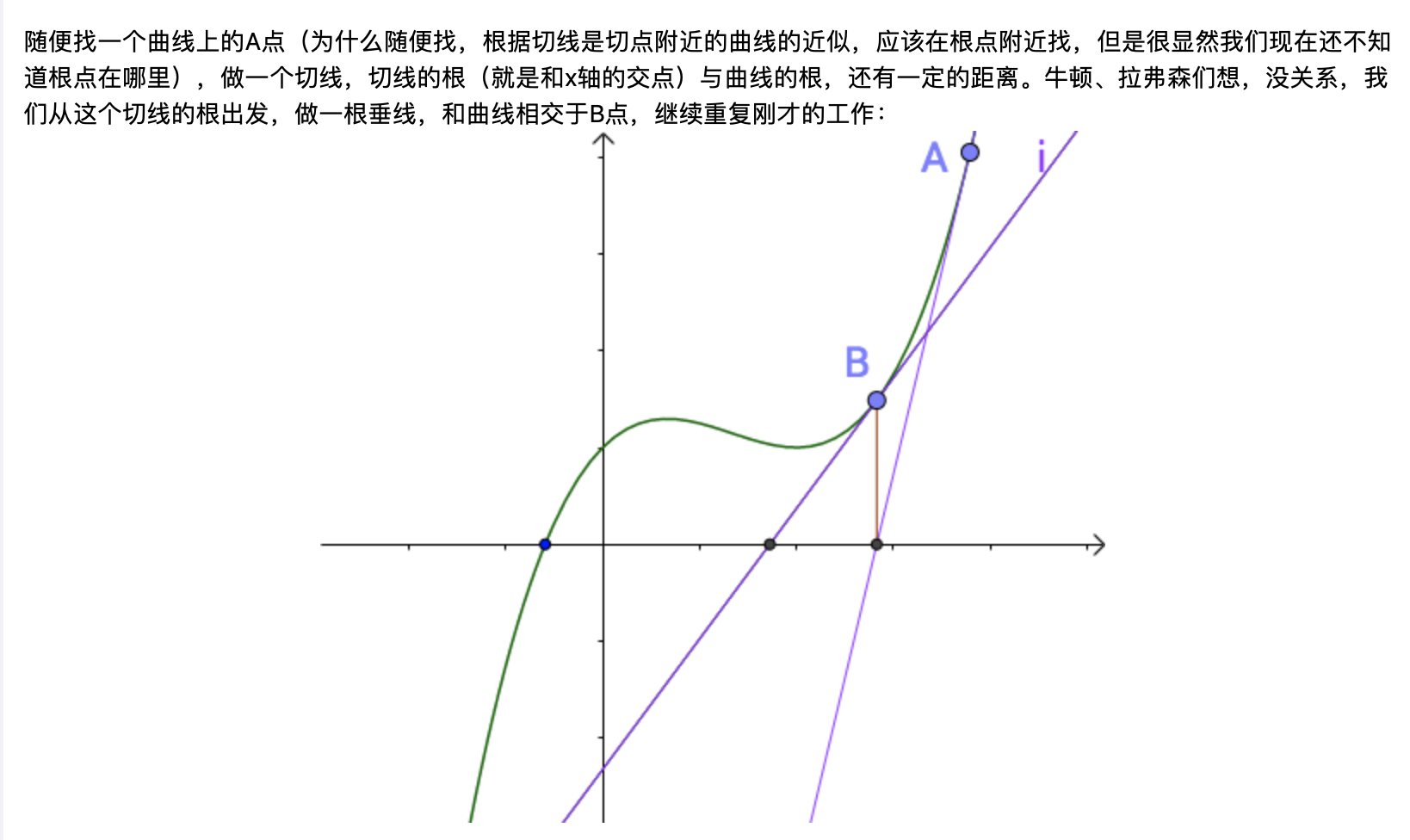
按点斜式求出直线方程（即过点Xn，f(Xn)），然后求出直线与x轴交点，即为Xn+1；



求a的平方根即求f(x)=x^2-a的正数解，由牛顿迭代法新一轮解Xn+1=(Xn+a/Xn)/2。

参考链接：https://www.matongxue.com/madocs/205.html

方法二：二分

从0到a/2+1二分查找平方根。

参考链接：https://leetcode-cn.com/problems/sqrtx/solution/er-fen-cha-zhao-niu-dun-fa-python-dai-ma-by-liweiw/

todo

实现方法二

方法一代码

class Solution {
    public int mySqrt(int x) {
        long ans=x;//随机初始化
        while(ans*ans>x){
            ans=(ans+x/ans)/2;
        }
        return (int)ans;
    }
}