C#数据结构-赫夫曼树

什么是赫夫曼树？

赫夫曼树(Huffman Tree)是指给定N个权值作为N个叶子结点，构造一棵二叉树，若该树的带权路径长度达到最小。哈夫曼树（也称为最优二叉树）是带权路径长度最短的树，权值较大的结点离根较近。

 1 　　 public class HNode<T>
 2     {
 3         public HNode()
 4         {
 5             data = default(T);
 6             weight = 0;
 7             leftNode = null;
 8             rightNode = null;
 9         }
10
11         public HNode(T val)
12         {
13             data = val;
14             weight = 0;
15             leftNode = null;
16             rightNode = null;
17         }
18
19         /// <summary>
20         /// 权重
21         /// </summary>
22         public int weight { get; set; }
23
24         /// <summary>
25         /// 内容
26         /// </summary>
27         public T data { get; set; }
28
29         /// <summary>
30         /// 左树
31         /// </summary>
32         public HNode<T> leftNode { get; set; }
33
34         /// <summary>
35         /// 右树
36         /// </summary>
37         public HNode<T> rightNode { get; set; }
38     }

 1 　　 /// <summary>
 2     /// 赫夫曼树
 3     /// </summary>
 4     /// <typeparam name="T"></typeparam>
 5     public class HTree<T>
 6     {
 7         /// <summary>
 8         /// 树的头结点
 9         /// </summary>
10         public HNode<T> head { get; set; }
11
12         /// <summary>
13         /// 构造函数
14         /// </summary>
15         /// <param name="val"></param>
16         public HTree(T val)
17         {
18             head = new HNode<T>(val);
19         }
20
21         public HTree()
22         {
23             head = new HNode<T>();
24         }
25         /// <summary>
26         /// 构建树结构
27         /// </summary>
28         /// <param name="list"></param>
29         public void build(List<T> list)
30         {
31             //判断是否能构建树结构
32             if (list == null || list.Count <2)
33                 throw new ArgumentOutOfRangeException("params error");
34             //分组统计
35             List<HNode<T>> nodes = new List<HNode<T>>();
36             nodes.AddRange(from m in list group m by m into g
37                            select new HNode<T> { data = g.Key,weight = g.Count()});
38             //排序
39             nodes = nodes.OrderBy(i => i.weight).ToList();
40
41             for (int i =1; i< nodes.Count; i++)
42             {
43                 HNode<T> parentNode = new HNode<T>();
44                 if (i == 1)
45                 {
46                     //先取最小的两个节点
47                     parentNode.leftNode = nodes[0];
48                     parentNode.rightNode = nodes[1];
49                     parentNode.weight = nodes[0].weight + nodes[1].weight;
50                 }
51                 else
52                 {
53                     //依次取节点构建树
54                     if (head.weight >= nodes[i].weight)
55                     {
56                         parentNode.leftNode = head;
57                         parentNode.rightNode = nodes[i];
58                     }
59                     else
60                     {
61                         parentNode.rightNode = head;
62                         parentNode.leftNode = nodes[i];
63                     }
64                     parentNode.weight = head.weight + nodes[i].weight;
65                 }
66                 head = parentNode;
67             }
68         }
69
70         /// <summary>
71         /// 先序遍历
72         /// </summary>
73         /// <param name="index"></param>
74         public void PreorderTraversal(HNode<T> node)
75         {
76             //递归的终止条件
77             if (head == null)
78             {
79                 Console.WriteLine("当前树为空");
80                 return;
81             }
82             if (node != null)
83             {
84                 if(node.data != null)
85                 Console.WriteLine($"{node.data} {node.weight}");
86                 PreorderTraversal(node.leftNode);
87                 PreorderTraversal(node.rightNode);
88             }
89         }
90     }

测试代码：

1 List<string> list = new List<string>() { "A","B", "B", "C", "C", "C", "D", "D", "D", "D", "E", "E", "E", "E", "E" };
2 HTree<string> tree = new HTree<string>();
3 tree.build(list);
4 tree.PreorderTraversal(tree.head);

打印结果：

A 1
B 2
C 3
D 4
E 5

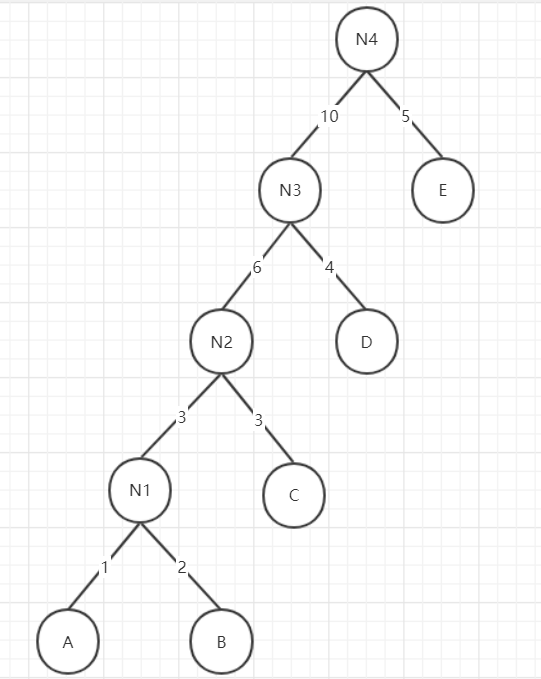
用这个例子现在我们看下构建的二叉树结构：

---