[GDKOI2021] 普及组 Day3 总结 && 题解

[ G D K O I 2021 ] 普 及 组 D a y 3 总 结

---

时间安排和昨天的GDKOI2021 Day2一样.

早上四个小时的快乐码题时间,然鹅我打了半小时的表
然后就是下午的题目讲解和凸包讲座.

---

题目讲解

---

T1

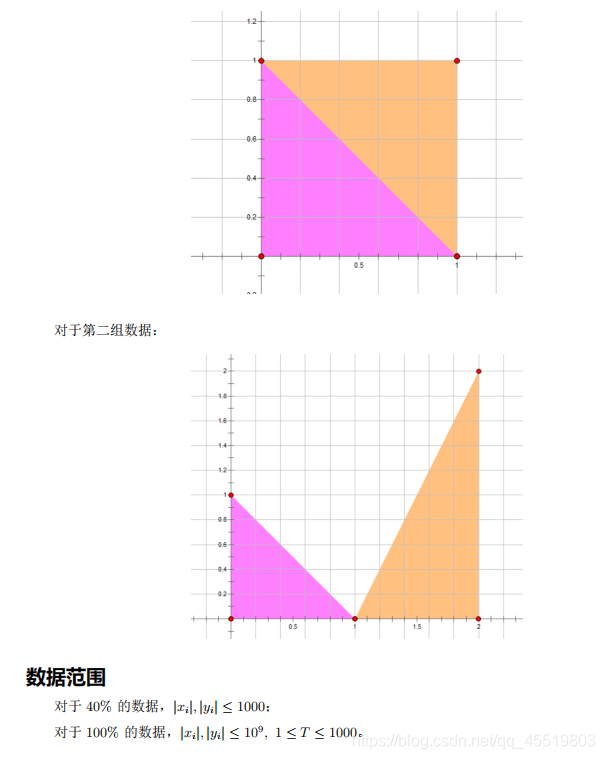
相似三角形的判定应该大家都知道,

一开始我还是用勾股来求的,结果打完后发现好像用欧氏距离简单的多…

关于我怎么用勾股来求边长的:

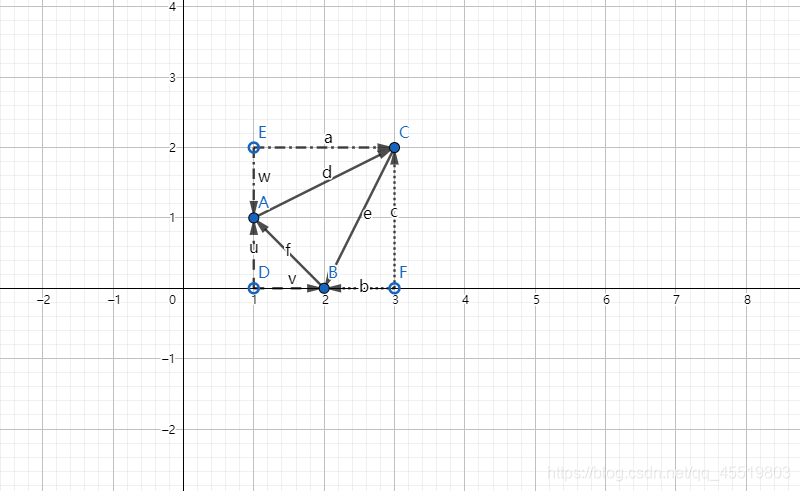
虚点是为了求边长而设定的辅助点,而实线是所求三角形的边.虚线是同辅助点建立的辅助边,由于是成

90

°

90°

90°的,所以可以用沟谷进行一个边的求长.因为知道了三角形三个点的位置,所以可以很容易地推导出符合这个要求的点,知道了辅助点和三角形的点的位置,又可以求出两条辅助边发的长度,然后就是勾股了.

---

T2

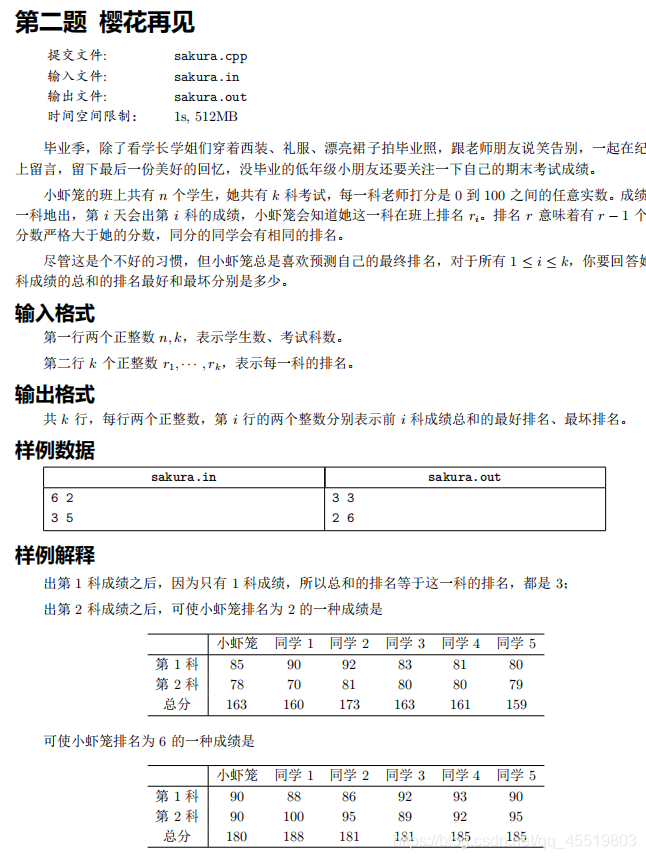
这题的思路很简单.由于成绩可能是任何实数,对于最优情况下就赋予99.99的成绩,比他高的(

r

−

1

r-1

r−1个)人就赋予

100分的成绩,比他低的就赋予0分的"好成绩".

对于最差的情况下,直接赋予最低的成绩,

0.如果没有人比他高,那么大家都是

0分,有比他高的都是100分,其他人都是  0分.

---

T3

出现了,Day 1讲过的数论
化简过程:

\begin{equation}
\sum_{k=1}^{n} \sum_{i \mid k} \sum_{j \mid i} \lambda(i) \lambda(j)=\sum_{k=1}^{n} \sum_{i \mid k} \lambda(i) \sum_{j \mid i} \lambda(j)
\end{equation}

我们设

\begin{equation}
\operatorname{sum}(x)=\sum_{i \mid x} \lambda(i)
\end{equation}

如果我们通过枚举

i
，相当于贡献就是

\begin{equation}
\lambda(i) * \operatorname{sum}(i)
\end{equation}

，显然在 1~n

内的每一个i的倍数都有一次贡献。这样可以拿到

60分的部分分。

如果仔细分析

\begin{equation}
\operatorname{sum}(x)
\end{equation}

的值可以发现，
如果

x
为完全平方数，

\begin{equation}
\operatorname{sum}(x)=1
\end{equation}

，否则

\begin{equation}
\operatorname{sum}(x)=0
\end{equation}

证明:分解

x的质因数,使

\begin{equation}
x=p_{1}^{a 1} * p_{1}^{a 1}
\end{equation}

。
显然每个指数

i从0到 a;取值的积就是

x
的每一个因数。
假设存在一个 α_k是奇数，那么这个质数的指数可以选择

0
到 a_k

，奇数个数刚好等于偶数个数，说明每一种选择都恰好有一种选择与它的指数和奇偶性想法，即\operatorname{sum}(x)=0
如果 a_i​全为偶数，即为完全平方数，那么
\operatorname{sum}(x)=1。由前面的对称性可以知道，如果将某个质数的指数减小

2，sum值不变。所有完全平方数的sum值等于
\operatorname{sum}(x)=1。

然后继续化简公式
\sum_{k=1}^{n} \sum_{i \mid k} \lambda(i) * \operatorname{sum}(i)
因为只有i是完全平方数时，
\operatorname{sum}(i)=1，而此时
\lambda(i)=1。那么答案就是每个完全平方数

x在

1
到

n
内的倍数的和。
即

\begin{equation}
\sum_{i^{2}<n} \frac{n}{i^{2}}
\end{equation}

---

T4

这道题有个很有意思的地方,就是序列前

i

i

i个元素的和要大于后

n

−

i

+

1

n-i+1

n−i+1个.这里由于

i

i

i是最小等于

1

1

1的,所以容易得出该要求的简化证明:该序列的第一个元素大于等于该序列其他元素之和才为题目定义的"好数列"
但如果就是不断地生成一个符合题目基本要求的序列,再去验证该序列是否为"好序列",那么通常会超出时限.于是我们就想到一个简化的思想

分析:
首先我们发现，如果某个长度为

i

i

i的前缀与长度为

i

i

i的后缀有重叠部分，那
么这个限制等价于长度为

n

−

i

n-i

n−i的前缀。也就是说如果

n

n

n是偶数，那么只需要
考虑前

n

/

2

n/2

n/2位满足条件即可;如果

n

n

n是奇数，也只需考虑

n

/

2

n/2

n/2位即可，中间
那一位可以随便填。
考虑一个计数

D

P

DP

DP,以

f

[

i

]

[

j

]

f[i][j]

f[i][j]来表示对于前

i

i

i位的和比后

i

i

i位大

j

j

j的方案数.
那么可以得出:

f

[

i

]

[

j

]

=

∑

k

=

m

a

x

(

j

−

n

,

0

)

j

+

n

f

[

i

]

[

k

]

∗

(

n

+

1

−

∣

j

−

k

∣

)

f[i][j]=\sum_{k=max(j-n,0)}^{j+n}f[i][k]*(n+1- \left | j-k \right |)

f[i][j]=k=max(j−n,0)∑j+n​f[i][k]∗(n+1−∣j−k∣)
时间复杂度为

O

(

n

4

)

O(n^4)

O(n4)

---

讲座

凸包

---

个人感想

这次

G

D

K

O

I

2021

GDKOI2021

GDKOI2021真的是教给了我很多,不论是讲堂还是讲题部分,都是有很多值得学习了了解的知识点的知识面的.
同今天解压密码一样,

G

D

K

O

I

GDKOI

GDKOI普及组,明年见