AOE网与关键路径
声明:图片及内容基于https://www.bilibili.com/video/BV1BZ4y1T7Yx?from=articleDetail
原理
AOE网


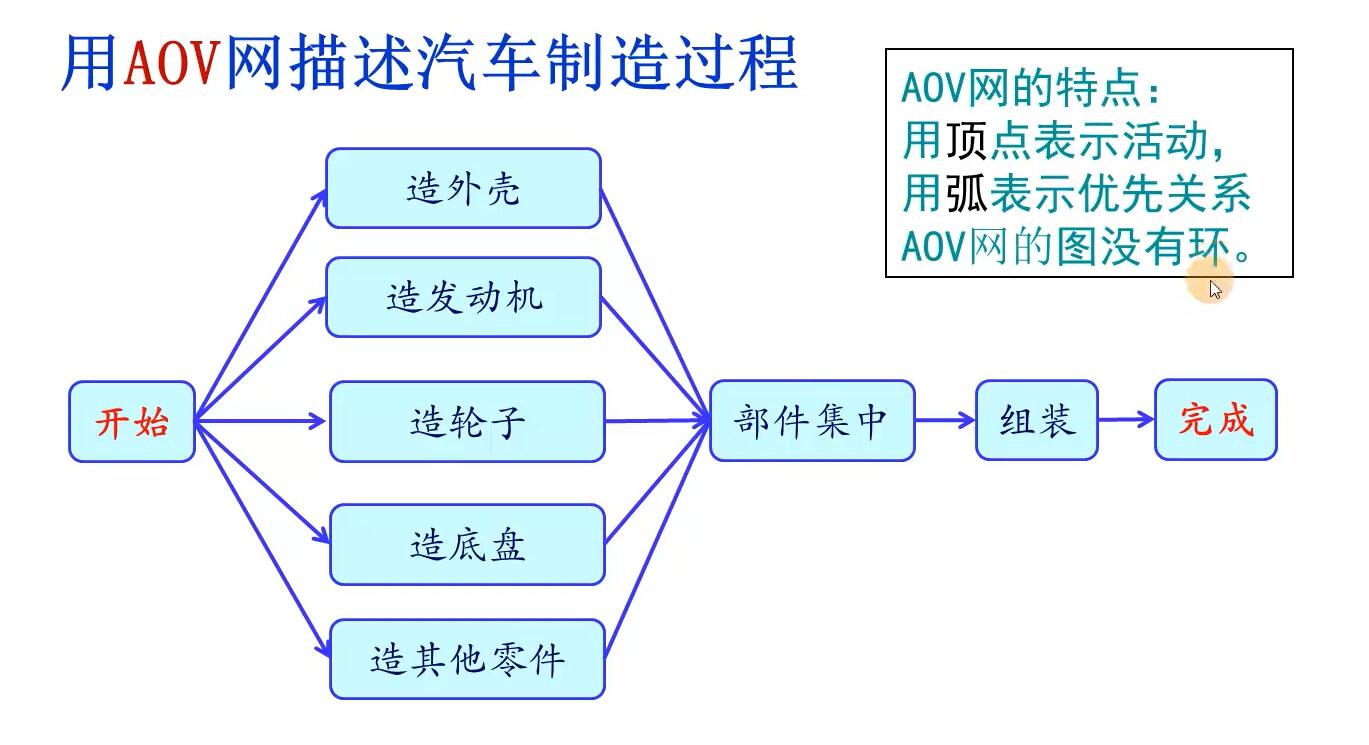

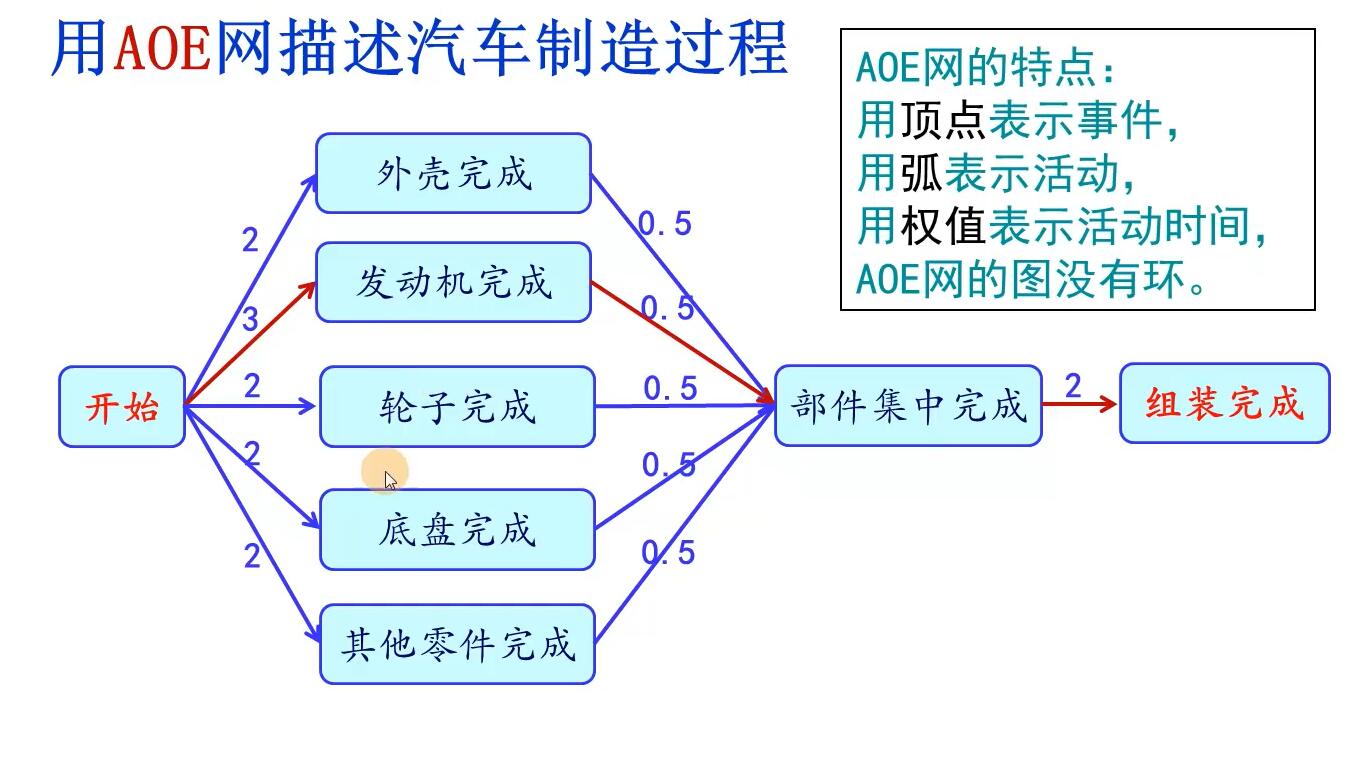
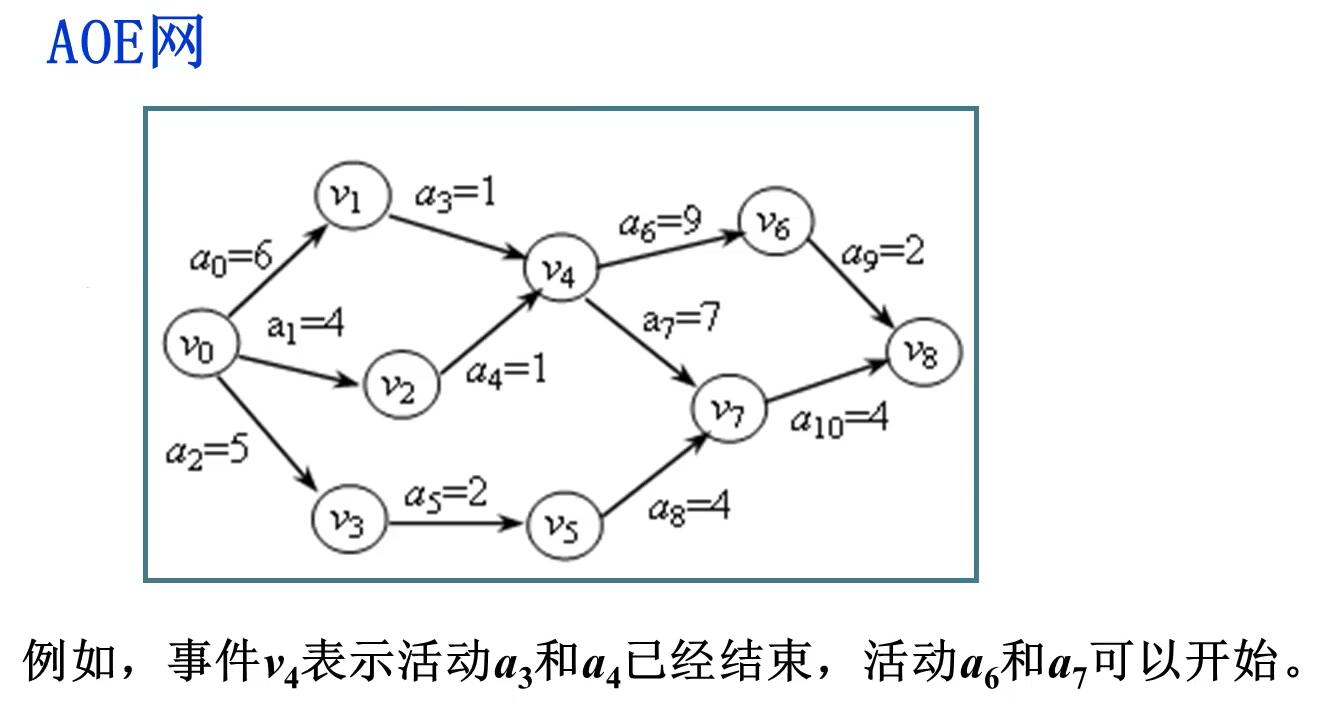
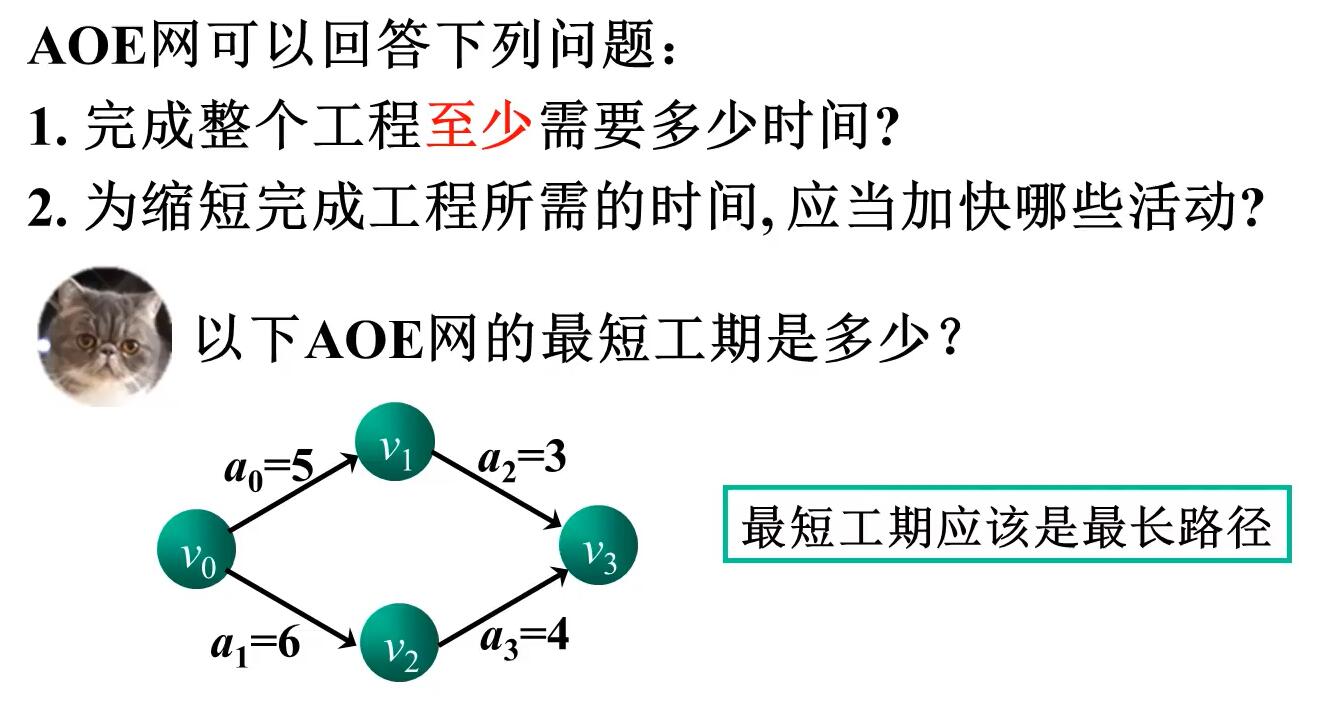
关键路径



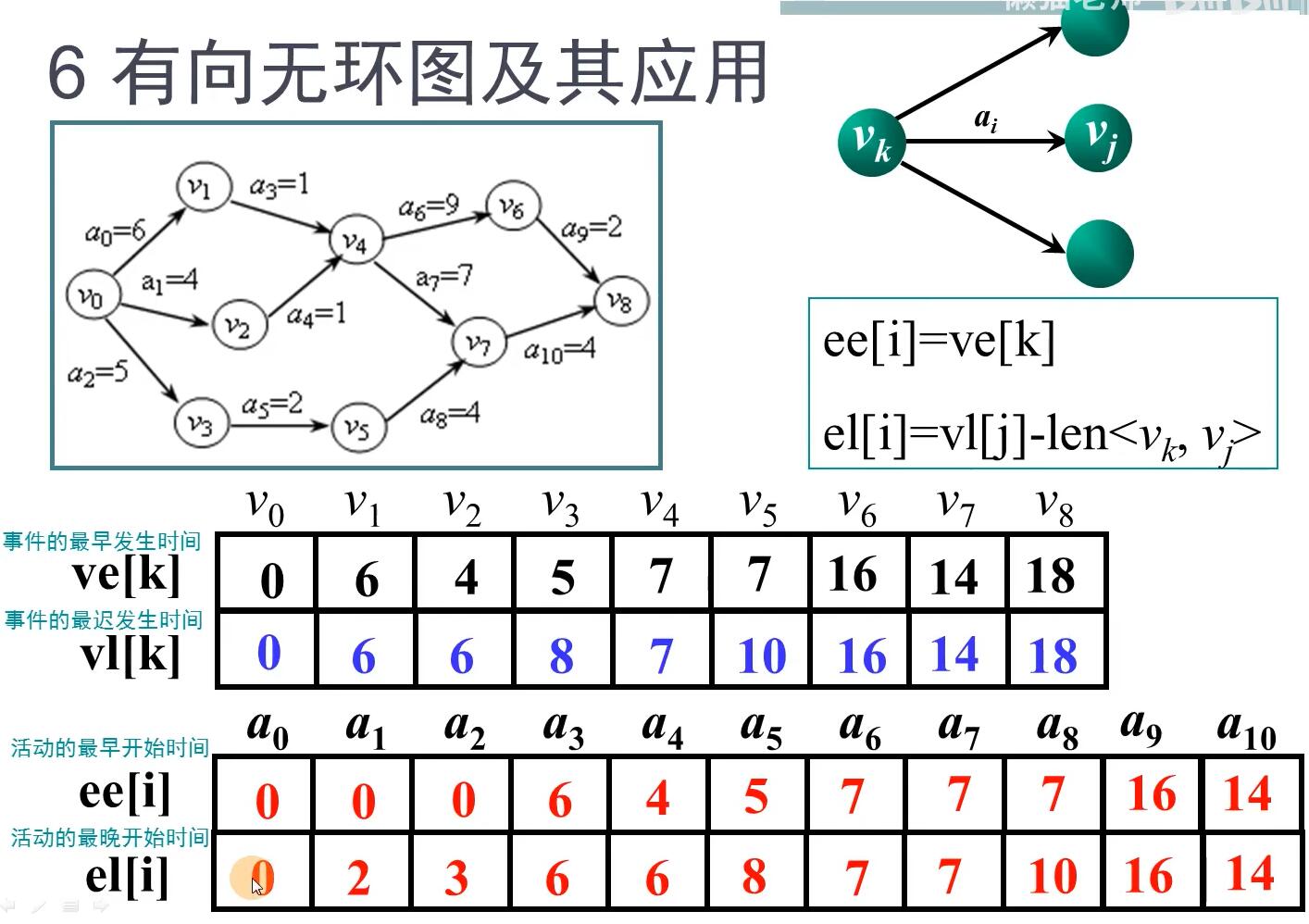
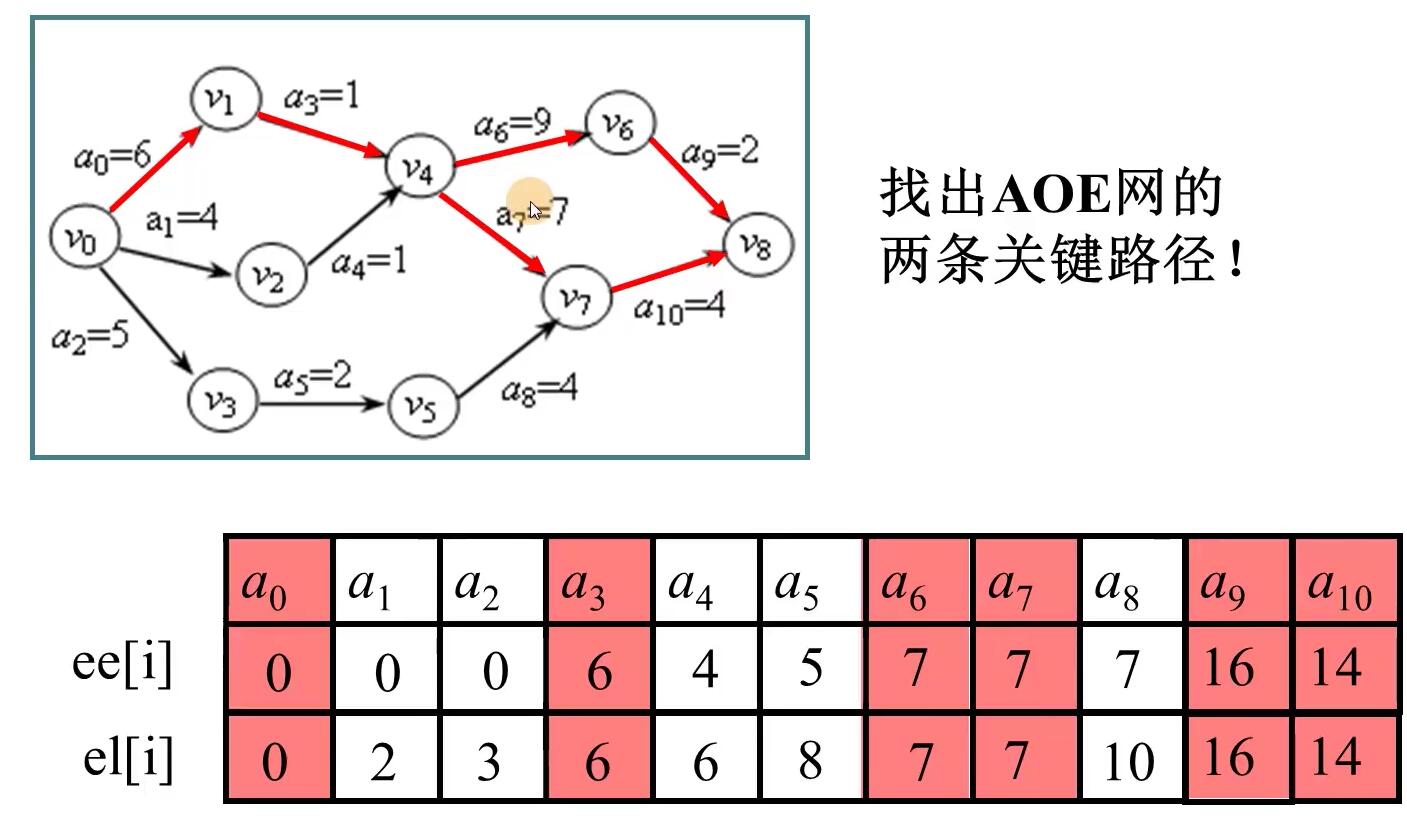

数据结构

核心代码
TopologicalSort
/*
TopologicalSort用于实现拓扑排序
参数:result用来保存处理过的拓扑排序顶点;count用来保存处理过的拓扑排序顶点的个数
功能:进行拓扑排序,将找到的拓扑顶点序号存入result数组(result可以看成一个栈,count可以看成是栈顶指针)
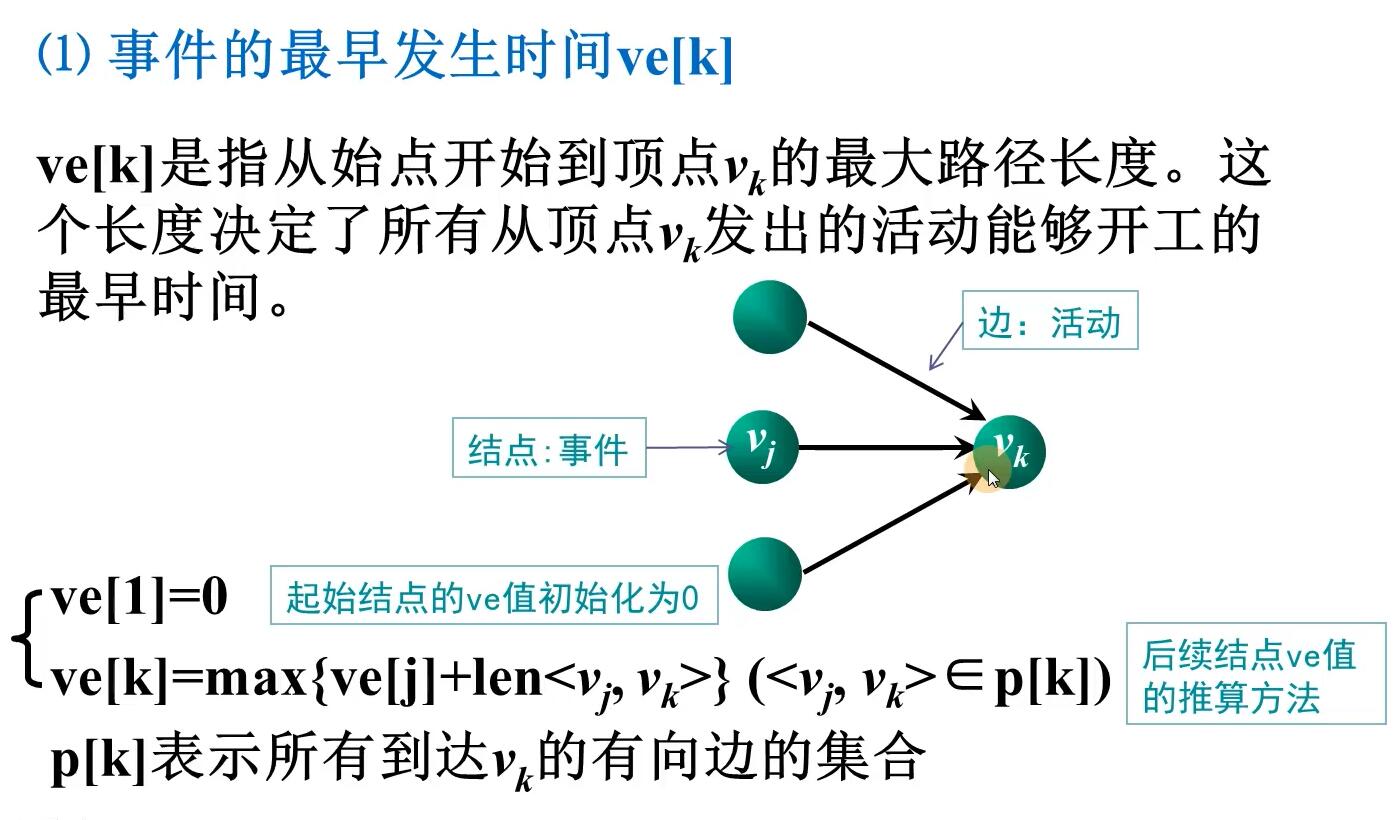
增加的功能:用注释=====标识,在拓扑排序的同时计算ve数组的值[事件最早发生时间]
*/
bool ALGraph ::TopologicalSort(int result[], int &count){ int stack[MAX_VERTEX]; //把顶点对应的下标压入堆栈 int top = -1;
int inVex; //用来保存从堆栈中弹出的顶点(下标)[书上的j,代表一个边的起始顶点]
int outVex;//遍历一个顶点的所有邻接边结点时,用outVex暂存当前处理的顶点[书上的k,代表一个边的终止顶点]
ArcNode *p; //初始化事件最早发生时间ve数组=====
for(int i=0;i<vertexNum;i++){
ve[i]=0;
}
//遍历顶点表,把入度为0的压栈
for(int i=0;i<vertexNum;i++){
if(adjList[i].in==0){
stack[++top]=i;
}
}
//完成拓扑排序
count=0;
while(top!=-1){
inVex=stack[top--];
result[count]=inVex;
count++;
p=adjList[inVex].firstEdge;
while(p){
outVex=p->adjvex;
adjList[outVex].in--;
if(adjList[outVex].in==0)
stack[++top]=outVex;
if(ve[inVex]+p->weight>ve[outVex])
ve[outVex]=ve[inVex]+p->weight;
p=p->next;
}
}
//判断拓扑排序是否正确
if(count==vertexNum)
return true;
return false;
}
CriticalPath
/*
CriticalPath用于求关键路径
首先调用TopologicalSort函数检查是否是一个没有环的图
*/
bool ALGraph::CriticalPath(){ int resultStack[MAX_VERTEX]; //存储拓扑排序结果序列(存储下标)
int resultTop; //拓扑排序有效顶点个数(栈顶指针)
ArcNode *p;
int i,count;
int inVex,outVex; //inVex,outVex,分别代表一条边的起点顶点号和终点顶点号 if(!TopologicalSort(resultStack,count)) {
return false;
} //输出拓扑排序的顶点处理顺序
cout<<"拓扑排序的顶点处理顺序是:"<<endl;
for(int i=0;i<count;i++){
cout<<resultStack[i]<<" ";
}
cout<<endl;
//输出ve数组的值
cout<<"ve数组的值为:"<<endl;
for(int i=0;i<count;i++){
cout<<"ve["<<i<<"]="<<ve[i]<<endl;
}
//完成关键路径的求解
resultTop=count-1;
inVex=resultStack[resultTop--];
for(int i=0;i<vertexNum;i++){
vl[i]=ve[inVex];
}
while(resultTop!=-1){
inVex=resultStack[resultTop--];
p=adjList[inVex].firstEdge;
while(p){
outVex=p->adjvex;
if(vl[inVex]>vl[outVex]-p->weight)
vl[inVex]=vl[outVex]-p->weight;
p=p->next;
}
}
cout<<"vl数组的值为:"<<endl;
for(int i=0;i<count;i++){
cout<<"vl["<<i<<"]="<<vl[i]<<endl;
}
return true;
}
完整代码
#include <iostream>
#include <stdio.h>
using namespace std; const int MAX_VERTEX = 30; //图的最大顶点数 struct ArcNode /*边表*/
{
int weight; //增加权值分量,代表活动时间=====
int adjvex;
ArcNode *next;
}; struct VertexNode /*顶点表*/
{
int in; //增加入度字段-----
char vertex;
ArcNode *firstEdge;
}; class ALGraph {
private:
VertexNode *adjList; //邻接表
int vertexNum, arcNum;
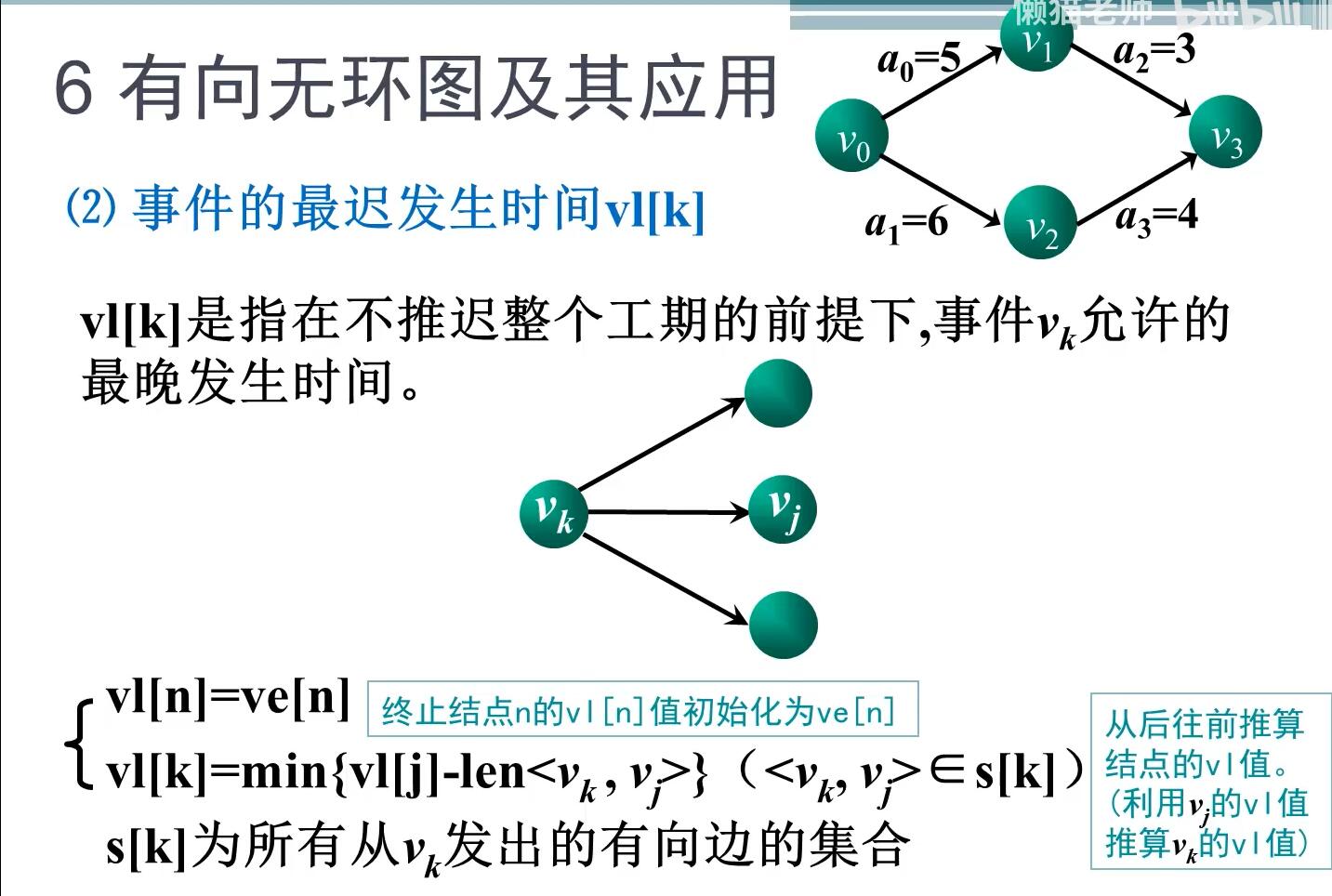
int *ve, *vl; //ve数组是事件最早发生时间,vl事件最迟发生时间(数组长度跟顶点数相等)=====
public:
ALGraph(char v[], int n, int e);
~ALGraph();
void inputEdges();
bool setEdge(int vi,int vj,int weight);
void displayData(); bool TopologicalSort(int result[], int &count); //拓扑排序
bool CriticalPath(); //求关键路径
}; ALGraph:: ALGraph(char v[], int n, int e){
vertexNum = n;
arcNum = e;
adjList = new VertexNode[vertexNum];
for (int i=0; i<vertexNum; i++) {
//输入顶点信息,初始化顶点表
adjList[i].in = 0; //增加in的初始化-----
adjList[i].vertex = v[i];
adjList[i].firstEdge = NULL;
}
ve = new int[vertexNum];
vl = new int[vertexNum]; }
ALGraph ::~ALGraph(){
ArcNode *p,*pre;
//遍历顶点表数组,把顶点表指向的所有边结点删除
for(int i=0; i<vertexNum; i++){
p = adjList[i].firstEdge;
adjList[i].firstEdge = NULL;
while(p){
pre = p;
p = p-> next;
delete pre;
}
}
delete [] adjList;
delete [] ve;
delete [] vl;
} void ALGraph ::inputEdges(){ //=====
cout << "请输入两个事件顶点编号(范围0-"<< vertexNum-1 << ")和活动时间:"<<endl;
for (int i=0; i<arcNum; i++) {
//输入边的信息存储在边表中
int vi,vj, weight;
cin >> vi >> vj >> weight; //输入边依附的两个顶点的编号
if(!setEdge(vi,vj,weight)){
cout << "输入的顶点编号超过范围或者相等,需要重新输入" << endl;
i--;
}
}
} bool ALGraph::setEdge(int vi,int vj, int weight){ //=====
//修改setEdge函数,把vj顶点表中的入度+1 -----
ArcNode *s;
if (vi>=0 && vi<vertexNum && vj>=0 && vj<vertexNum && vi!=vj){
//创建一个边结点vj
s = new ArcNode;
s->adjvex = vj;
s->weight = weight; //=====
//把边结点vj插入到顶点表vi项的邻接表中,成为第一个结点
s->next = adjList[vi].firstEdge;
adjList[vi].firstEdge = s;
//vj顶点表中的入度+1 -----
adjList[vj].in++;
return true;
}
else {
return false;
}
} void ALGraph ::displayData(){
ArcNode *p;
cout << "输出图的存储情况:"<<endl;
for(int i=0; i<vertexNum; i++){
cout << "顶点" << adjList[i].vertex << "的入度为:" << adjList[i].in <<",从这个顶点发出的的边为:" << endl;//-----
p = adjList[i].firstEdge;
if (!p)
cout << "没有。"<< endl;
while(p){
cout <<"<" << i <<"," << p->adjvex<< ">" << p->weight <<endl;
p = p->next;
}
}
}
/*
TopologicalSort用于实现拓扑排序
参数:result用来保存处理过的拓扑排序顶点;count用来保存处理过的拓扑排序顶点的个数
功能:进行拓扑排序,将找到的拓扑顶点序号存入result数组(result可以看成一个栈,count可以看成是栈顶指针)
增加的功能:用注释=====标识,在拓扑排序的同时计算ve数组的值[事件最早发生时间]
*/
bool ALGraph ::TopologicalSort(int result[], int &count){ int stack[MAX_VERTEX]; //把顶点对应的下标压入堆栈 int top = -1;
int inVex; //用来保存从堆栈中弹出的顶点(下标)[书上的j,代表一个边的起始顶点]
int outVex;//遍历一个顶点的所有邻接边结点时,用outVex暂存当前处理的顶点[书上的k,代表一个边的终止顶点]
ArcNode *p; //初始化事件最早发生时间ve数组=====
for(int i=0;i<vertexNum;i++){
ve[i]=0;
}
//遍历顶点表,把入度为0的压栈
for(int i=0;i<vertexNum;i++){
if(adjList[i].in==0){
stack[++top]=i;
}
}
//完成拓扑排序
count=0;
while(top!=-1){
inVex=stack[top--];
result[count]=inVex;
count++;
p=adjList[inVex].firstEdge;
while(p){
outVex=p->adjvex;
adjList[outVex].in--;
if(adjList[outVex].in==0)
stack[++top]=outVex;
if(ve[inVex]+p->weight>ve[outVex])
ve[outVex]=ve[inVex]+p->weight;
p=p->next;
}
}
//判断拓扑排序是否正确
if(count==vertexNum)
return true;
return false;
} /*
CriticalPath用于求关键路径
首先调用TopologicalSort函数检查是否是一个没有环的图
*/
bool ALGraph::CriticalPath(){ int resultStack[MAX_VERTEX]; //存储拓扑排序结果序列(存储下标)
int resultTop; //拓扑排序有效顶点个数(栈顶指针)
ArcNode *p;
int i,count;
int inVex,outVex; //inVex,outVex,分别代表一条边的起点顶点号和终点顶点号 if(!TopologicalSort(resultStack,count)) {
return false;
} //输出拓扑排序的顶点处理顺序
cout<<"拓扑排序的顶点处理顺序是:"<<endl;
for(int i=0;i<count;i++){
cout<<resultStack[i]<<" ";
}
cout<<endl;
//输出ve数组的值
cout<<"ve数组的值为:"<<endl;
for(int i=0;i<count;i++){
cout<<"ve["<<i<<"]="<<ve[i]<<endl;
}
//完成关键路径的求解
resultTop=count-1;
inVex=resultStack[resultTop--];
for(int i=0;i<vertexNum;i++){
vl[i]=ve[inVex];
}
while(resultTop!=-1){
inVex=resultStack[resultTop--];
p=adjList[inVex].firstEdge;
while(p){
outVex=p->adjvex;
if(vl[inVex]>vl[outVex]-p->weight)
vl[inVex]=vl[outVex]-p->weight;
p=p->next;
}
}
cout<<"vl数组的值为:"<<endl;
for(int i=0;i<count;i++){
cout<<"vl["<<i<<"]="<<vl[i]<<endl;
}
return true;
} int main(){
char vertex[MAX_VERTEX];
int num,edge; cout << "请输入顶点个数和边的个数:";
cin >> num >> edge;
for(int i=0; i<num; i++)
vertex[i] = i + '0'; ALGraph graph(vertex,num,edge);
graph.inputEdges();
graph.displayData(); if(!graph.CriticalPath()){
cout << "这个图有回路,不能求关键路径。";
} //记住,main函数调用结束后,会自动调用析构函数,对图的数据以及ve,vl数组进行释放。 return 0;
}
输入:
9 11
0 1 6
0 2 4
0 3 5
1 4 1
2 4 1
3 5 2
4 6 9
4 7 7
5 7 4
6 8 2
7 8 4
输出:
输出图的存储情况:
顶点0的入度为:0,从这个顶点发出的的边为:
<0,3>5
<0,2>4
<0,1>6
顶点1的入度为:1,从这个顶点发出的的边为:
<1,4>1
顶点2的入度为:1,从这个顶点发出的的边为:
<2,4>1
顶点3的入度为:1,从这个顶点发出的的边为:
<3,5>2
顶点4的入度为:2,从这个顶点发出的的边为:
<4,7>7
<4,6>9
顶点5的入度为:1,从这个顶点发出的的边为:
<5,7>4
顶点6的入度为:1,从这个顶点发出的的边为:
<6,8>2
顶点7的入度为:2,从这个顶点发出的的边为:
<7,8>4
顶点8的入度为:2,从这个顶点发出的的边为:
没有。
拓扑排序的顶点处理顺序是:
0 1 2 4 6 3 5 7 8
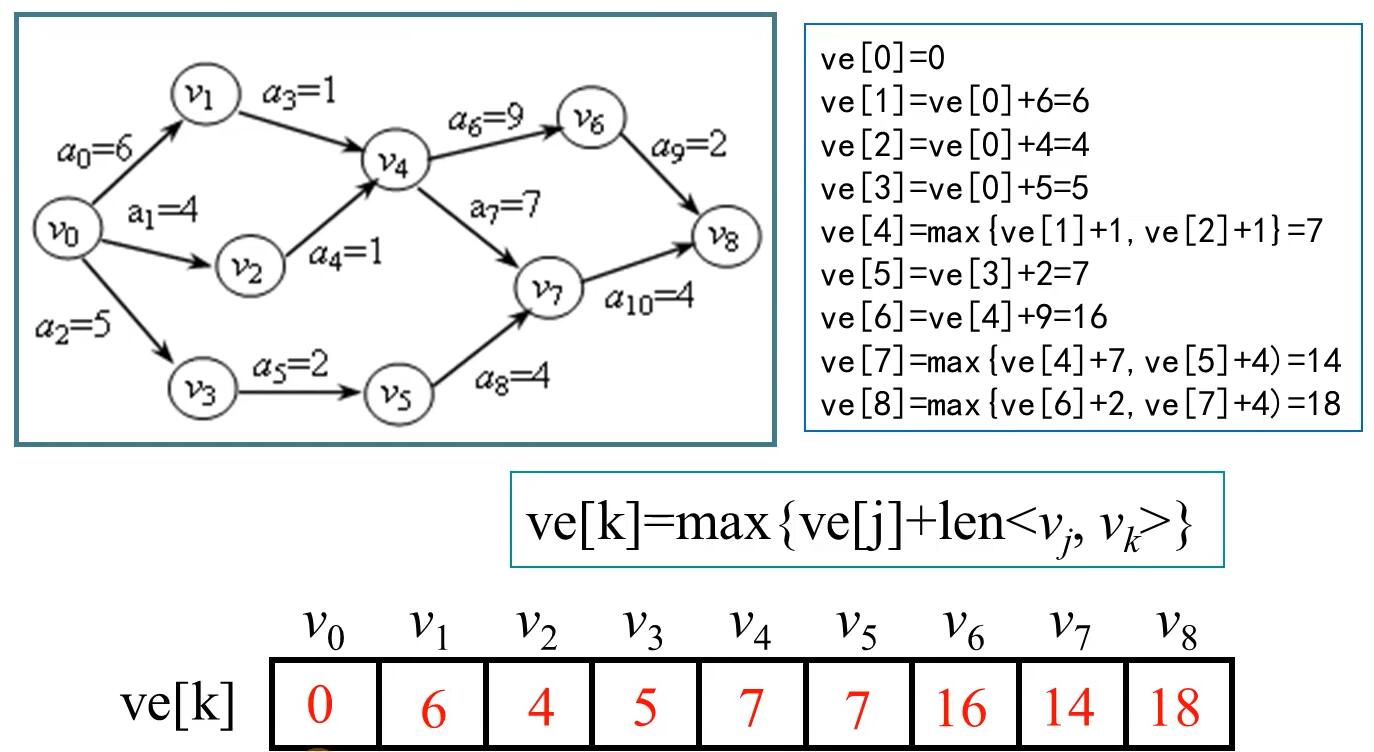
ve数组的值为:
ve[0]=0
ve[1]=6
ve[2]=4
ve[3]=5
ve[4]=7
ve[5]=7
ve[6]=16
ve[7]=14
ve[8]=18
vl数组的值为:
vl[0]=0
vl[1]=6
vl[2]=6
vl[3]=8
vl[4]=7
vl[5]=10
vl[6]=16
vl[7]=14
vl[8]=18
AOE网与关键路径的更多相关文章
- AOE网与关键路径简介
前面我们说过的拓扑排序主要是为解决一个工程能否顺序进行的问题,但有时我们还需要解决工程完成需要的最短时间问题.如果我们要对一个流程图获得最短时间,就必须要分析它们的拓扑关系,并且找到当中最关键的流程, ...
- 基于AOE网的关键路径的求解
[1]关键路径 在我的经验意识深处,“关键”二字一般都是指临界点. 凡事万物都遵循一个度的问题,那么存在度就会自然有临界点. 关键路径也正是研究这个临界点的问题. 在学习关键路径前,先了解一个AOV网 ...
- _DataStructure_C_Impl:AOE网的关键路径
//_DataStructure_C_Impl:CriticalPath #include<stdio.h> #include<stdlib.h> #include<st ...
- AOE网的关键路径的计算
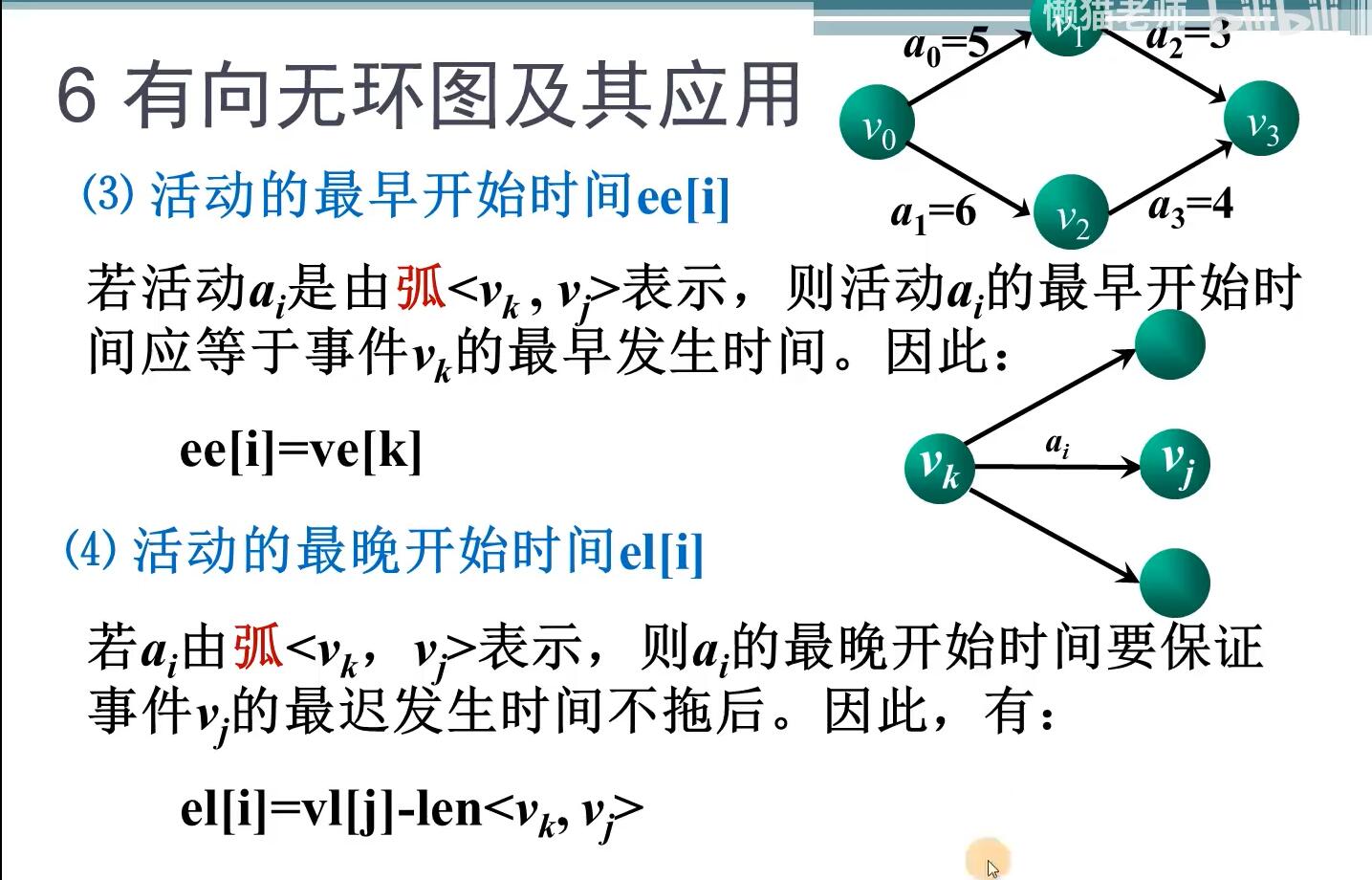
求关键路径,只需理解顶点(事件)和边(活动)各自的两个特征属性以及求法即可: Ø 先根据首结点的Ve(j)=0由前向后(正拓扑序列)计算各顶点的最早发生时间 Ø 再根据终结点的Vl(j)等于它的V ...
- 教你轻松计算AOE网关键路径(转)
原文链接:http://blog.csdn.net/wang379275614/article/details/13990163 本次结合系统分析师-运筹方法-网络规划技术-关键路径章节,对原文链接描 ...
- 教你轻松计算AOE网关键路径
认识AOE网 有向图中,用顶点表示活动,用有向边表示活动之间开始的先后顺序,则称这种有向图为AOV网络:AOV网络可以反应任务完成的先后顺序(拓扑排序). 在AOV网的边上加上权值表示完成该活动所需的 ...
- SDUT 2498 AOE网上的关键路径
AOE网上的关键路径 Time Limit: 1000MS Memory Limit: 65536KB Submit Statistic Problem Description 一个无环的有向图称为无 ...
- 数据结构关于AOV与AOE网的区别
AOV网,顶点表示活动,弧表示活动间的优先关系的有向图. 即如果a->b,那么a是b的先决条件. AOE网,边表示活动,是一个带权的有向无环图, 其中顶点表示事件,弧表示活动,权表示活动持续时间 ...
- AOV图与拓扑排序&AOE图与关键路径
AOV网:所有的工程或者某种流程可以分为若干个小的工程或阶段,这些小的工程或阶段就称为活动.若以图中的顶点来表示活动,有向边表示活动之间的优先关系,则这样活动在顶点上的有向图称为AOV网. 拓扑排序算 ...
随机推荐
- js animation & requestAnimationFrame
js animation & requestAnimationFrame https://developer.mozilla.org/en-US/docs/Web/API/window/req ...
- Flutter: The getter 'futureDynamicType' was called on null.
> flutter packages pub upgrade
- 能取值亦能赋值的Python切片
切片,就像面包,给几刀,切成一片一片,可以做成吐司,也可以做成三明治,口味更佳: 列表(list).元组(tuple).字符串(str)都能进行切片,得到子片段,实际上切片操作比想象的要强大很多,能取 ...
- FTP返回值代表含义
FTP:屏幕信息举例 1.用户要用FTP和远地主机(网络信息中心NIC上的主机)建立连接. 2.本地FTP发出的连接成功信息. 3.从远地服务器返回的信息,220表示"服务就绪". ...
- javaMail (java代码发送邮件)
第一在邮件账户设置开启以下两个 需要发送短信获取 授权码. 代码如下: package com.hjb.javaMail; import javax.mail.*; import javax.mai ...
- 后端程序员之路 43、Redis list
Redis数据类型之LIST类型 - Web程序猿 - 博客频道 - CSDN.NEThttp://blog.csdn.net/thinkercode/article/details/46565051 ...
- .net 开源模板引擎jntemplate 教程:基础篇之语法
一.基本概念 上一篇我们简单的介绍了jntemplate并写了一个hello world(如果没有看过的,点击查看),本文将继续介绍jntemplate的模板语法. 我们在讲解语法前,首先要了解一下标 ...
- Codeforces1493D GCD of an Array
题目链接 点我跳转 题目大意 给定一个长度为 \(N\) 的序列 \(A\) 有 \(Q\) 次操作,每次操作给定两个数 \(i\) , \(X\),使得 \(A[i] = A[i] \times X ...
- 大数据实战-Hive-技巧实战
1.union 和 union all 前者可以去重 select sex,address from test where dt='20210218' union all select sex,add ...
- go中waitGroup源码解读
waitGroup源码刨铣 前言 WaitGroup实现 noCopy state1 Add Wait 总结 参考 waitGroup源码刨铣 前言 学习下waitGroup的实现 本文是在go ve ...
