Python学习之多项式回归

本文的文字及图片来源于网络,仅供学习、交流使用,不具有任何商业用途,如有问题请及时联系我们以作处理

线性回归的改进版本中的多项式回归。如果您知道线性回归，那么对您来说很简单。如果没有，我将在本文中解释这些公式。还有其他先进且更有效的机器学习算法。但是，学习基于线性的回归技术是一个好主意。因为它们简单，快速并且可以使用众所周知的公式。尽管它可能不适用于复杂的数据集。

多项式回归公式

仅当输入变量和输出变量之间存在线性相关性时，线性回归才能很好地执行。如前所述，多项式回归建立在线性回归的基础上。如果您需要线性回归的基础知识，请访问线性回归：

Python中的线性回归算法

学习线性回归的概念并从头开始在python中开发完整的线性回归算法

多项式回归可以更好地找到输入要素与输出变量之间的关系，即使该关系不是线性的。它使用与线性回归相同的公式：

Y = BX + C

我敢肯定，我们都在学校学过这个公式。对于线性回归，我们使用如下符号：

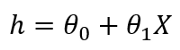
在这里，我们从数据集中获得X和Y。X是输入要素，Y是输出变量。Theta值是随机初始化的。

对于多项式回归，公式如下所示：

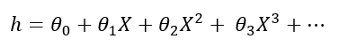
我们在这里添加更多术语。我们使用相同的输入功能，并采用不同的指数以制作更多功能。这样，我们的算法将能够更好地了解数据。

幂不必为2、3或4。它们也可以为1 / 2、1 / 3或1/4。然后，公式将如下所示：

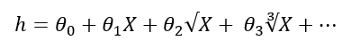
成本函数和梯度下降

成本函数给出了预测假设与值之间的距离的概念。公式为：

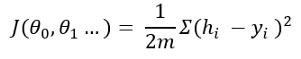
这个方程可能看起来很复杂。它正在做一个简单的计算。首先，从原始输出变量中减去假设。取平方消除负值。然后将该值除以训练示例数量的2倍。

什么是梯度下降?它有助于微调我们随机初始化的theta值。我不打算在这里进行微积分。如果对每个θ取成本函数的偏微分，则可以得出以下公式：

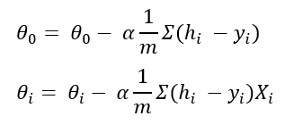
在这里，alpha是学习率。您选择alpha的值。

多项式回归的Python实现

这是多项式回归的逐步实现。

(1) 在此示例中，我们将使用一个简单的虚拟数据集，该数据集提供职位的薪水数据。导入数据集：

import pandas as pd 
import numpy as np 
df = pd.read_csv('position_salaries.csv') 
df.head() 

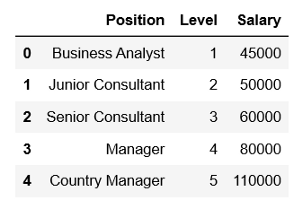
(2) 添加theta 0的偏差列。该偏差列将仅包含1。因为如果将1乘以数字，则它不会改变。

df = pd.concat([pd.Series(1, index=df.index, name='00'), df], axis=1) 
df.head() 

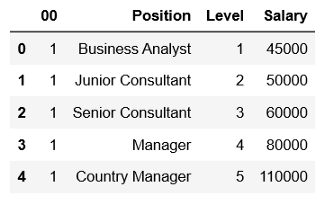
(3) 删除"位置"列。由于"位置"列中包含字符串，并且算法无法理解字符串。我们有"级别"列来代表职位。

dfdf = df.drop(columns='Position') 

(4) 定义我们的输入变量X和输出变量y。在此示例中，"级别"是输入功能，而"薪水"是输出变量。我们要预测各个级别的薪水。

y = df['Salary']X = df.drop(columns = 'Salary') 
X.head() 

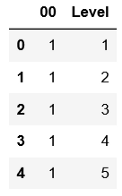
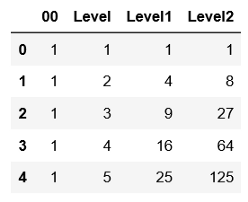
(5) 以"级别"列的指数为基础，创建"级别1"和"级别2"列。

X['Level1'] = X['Level']**2 
X['Level2'] = X['Level']**3 
X.head() 

(6) 现在，标准化数据。用每一列除以该列的最大值。这样，我们将获得每列的值，范围从0到1。即使没有规范化，该算法也应该起作用。但这有助于收敛更快。同样，计算m的值，它是数据集的长度。

m = len(X) 
XX = X/X.max() 

(7) 定义假设函数。这将使用X和theta来预测" y"。

def hypothesis(X, theta):  
  y1 = theta*X  
  return np.sum(y1, axis=1) 

(8) 使用上面的成本函数公式定义成本函数：

def cost(X, y, theta):  
  y1 = hypothesis(X, theta)  
  return sum(np.sqrt((y1-y)**2))/(2*m) 

(9) 编写梯度下降函数。我们将不断更新theta值，直到找到最佳成本。对于每次迭代，我们将计算成本以供将来分析。

def gradientDescent(X, y, theta, alpha, epoch): 
    J=[] 
    k=0 
    while k < epoch: 
        y1 = hypothesis(X, theta) 
        for c in range(0, len(X.columns)): 
            theta[c] = theta[c] - alpha*sum((y1-y)* X.iloc[:, c])/m 
        j = cost(X, y, theta) 
        J.append(j) 
        k += 1 
    return J, theta 

(10) 定义了所有功能。现在，初始化theta。我正在初始化零数组。您可以采用任何其他随机值。我选择alpha为0.05，我将迭代700个纪元的theta值。

theta = np.array([0.0]*len(X.columns)) 
J, theta = gradientDescent(X, y, theta, 0.05, 700) 

(11) 我们还获得了最终的theta值以及每次迭代的成本。让我们使用最终theta查找薪水预测。

y_hat = hypothesis(X, theta) 

(12) 现在根据水平绘制原始薪水和我们的预期薪水。

%matplotlib inline 
import matplotlib.pyplot as plt 
plt.figure() 
plt.scatter(x=X['Level'],yy= y)            
plt.scatter(x=X['Level'], y=y_hat) 
plt.show() 

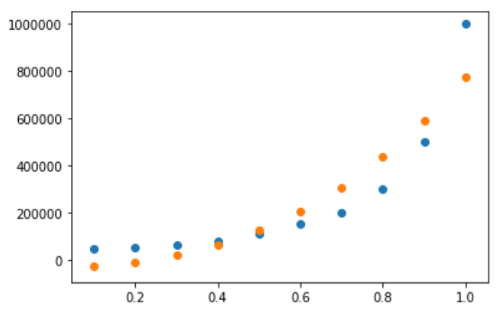
我们的预测并不完全符合薪资趋势，但接近。线性回归只能返回一条直线。但是在多项式回归中，我们可以得到这样的曲线。如果该线不是一条好曲线，则多项式回归也可以学习一些更复杂的趋势。

(13) 让我们绘制我们在梯度下降函数中每个时期计算的成本。

plt.figure() 
plt.scatter(x=list(range(0, 700)), y=J) 
plt.show() 

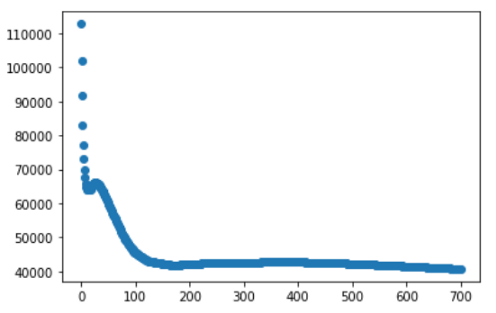
成本从一开始就急剧下降，然后下降缓慢。在一个好的机器学习算法中，成本应该一直下降直到收敛。请随意尝试不同的时期和不同的学习率(alpha)。

这是数据集：salary_data https://github.com/rashida048/Machine-Learning-With-Python/blob/master/position_salaries.csv

想要获取更多Python学习资料可以加
QQ:2955637827私聊
或加Q群630390733
大家一起来学习讨论吧！