游戏寻路A*算法

A*算法是一种启发式的BFS，目的就是找到到达目标位置的最短路径。启发式函数如下：

f(x) = g(x) + h(x)

g(x)是对出发点到达当前点距离的估约，h(x)是当前点到终点距离的估约。算法是一个广度优先搜索的过程，但是搜索时的可选集合是一个优先级队列，f(x)越小优先级越高。

算法过程描述

1。用起点初始优先级队列opened；

2。在opened中取最小f(x)的坐标节点，如果该点就是终点，则成功找到返回，否则，向该点的相邻方向寻找可行的下一个移动节点，计算每一个可行节点的f(x)保存，放入opened队列中，继续步骤2；

关于最短路径的求解还应该维护一个映射表，保存移动过程的上一个节点，之后再从终点往前遍历到起点便是整条路径了。

求单源最短路径的迪杰斯特拉算法其实就是当h(x)=0的A*算法。以下是算法的伪码（摘自维基百科）

function A*(start,goal)
    closedset := the empty set    // The set of nodes already evaluated.
    openset := {start}    // The set of tentative nodes to be evaluated, initially containing the start node
    came_from := the empty map    // The map of navigated nodes.
 
    g_score[start] := 0    // Cost from start along best known path.
    // Estimated total cost from start to goal through y.
    f_score[start] := g_score[start] + heuristic_cost_estimate(start, goal)
 
    while openset is not empty
        current := the node in openset having the lowest f_score[] value
        if current = goal
            return reconstruct_path(came_from, goal)
 
        remove current from openset
        add current to closedset
        for each neighbor in neighbor_nodes(current)
            tentative_g_score := g_score[current] + dist_between(current,neighbor)
            tentative_f_score := tentative_g_score + heuristic_cost_estimate(neighbor, goal)
            if neighbor in closedset and tentative_f_score >= f_score[neighbor]
                    continue
 
            if neighbor not in openset or tentative_f_score < f_score[neighbor]
                came_from[neighbor] := current
                g_score[neighbor] := tentative_g_score
                f_score[neighbor] := tentative_f_score
                if neighbor not in openset
                    add neighbor to openset
 
    return failure

详细设计实现

游戏中自动寻路的场景会被划分成网格，每一个网格可以是阻挡或者通路，在当前网格中可以向周围8个相邻方向移动（左，右，上，下，左上，左下，右上，右下）。运用A*算法从start寻路到end，启发式函数可以这样设计：

1。g(x)设计：初始化起点的g(start) = 0。假设当前位置是cur，下一个位置next若是cur从对角移动过来的（即左上，左下，右上，右下）则g(next) = g(cur) + 14，若是从水平或者垂直方向移动过来的，则g(next) = g(cur) + 10。常数14和10是这么得来的：勾股定理中，假设两直角边都是1,对角线则是1.414，各自放大10倍取整就是10和14；

2。h(x)设计：假设当前节点是（xcur，ycur），终点是（xend，yend），h(x) = abs(xcur – xend) + abs(ycur- yend)；

优先级队列可以用最小堆来实现，但是搜索过程中可能出现这样的情况：新添加一个可用节点时，该节点已经在opened队列中了，且新节点有更小的f(x)值，这时候要更新队列中这个节点并重新调整堆。查找新入的节点是否已经在队列中了，单纯用最小堆实现时间复杂度是O(n)，可以再加一个hash表，维护坐标点到最小堆中节点的映射，复杂度降为O(1)。代码实现如下：

#define TI(x, y) ((x)*H+(y))
 
struct OpenedNode{
	int _f, _g;
	int _x, _y;
	int _parent;
	OpenedNode(int f = -1, int g = -1, int x = -1, int y = -1, int parent = -1):_f(f),_g(g),_x(x),_y(y),_parent(parent) {}
 
};
 
template <size_t W, size_t H>
class OpenedHeap {
	OpenedNode _heap[W*H];
	int _set[W*H];
	int _sz;
 
	void move_top(int icur) {
		OpenedNode ON = _heap[icur];
		while (icur > 0) {
			int iparent = (icur-1) / 2;
			if (_heap[iparent]._f <= ON._f) break;
 
			_heap[icur]	   = _heap[iparent];
 
			// update
			_set[TI(_heap[icur]._x,_heap[icur]._y)] = icur;
 
			icur = iparent;
		}
		_heap[icur] = ON;
		_set[TI(_heap[icur]._x, _heap[icur]._y)] = icur;
	}
 
	void move_bottom(int icur) {
		OpenedNode ON = _heap[icur];
		while (true) {
			int ileft = icur * 2 + 1;
			if (ileft >= _sz) break;
 
			int iright = icur * 2 + 2;
 
			int ismaller = iright < _sz && _heap[iright]._f < _heap[ileft]._f? iright:ileft;
 
			if (_heap[ismaller]._f < ON._f) {
				_heap[icur] = _heap[ismaller];
				_set[TI(_heap[icur]._x, _heap[icur]._y)] = icur;
				icur = ismaller;
			}else break;
		}
		_heap[icur] = ON;
		_set[TI(_heap[icur]._x, _heap[icur]._y)] = icur;
	}
 
public:
	OpenedHeap():_sz(0) {
		memset(_set, -1, sizeof(_set));
	}
 
	void push(const OpenedNode &ON) {
		_heap[_sz] = ON;
		int icur = _sz++;
 
		move_top(icur);
	//	ensure();
	}
 
	void pop(OpenedNode &ret) {
		ret = _heap[0];
		_set[TI(_heap[0]._x,_heap[0]._y)] = -1;
		assert(_sz>0);
		_heap[0] = _heap[--_sz];
		if (_sz > 0)
			move_bottom(0);
//		ensure();
	}
 
	bool Get(int x, int y, OpenedNode &ret) {
		if (_set[TI(x,y)] >= 0) {
			ret = _heap[_set[TI(x,y)]];
			return true;
		}
		return false;
	}
 
	bool make_smaller(int x, int y, int f, int g, int parent) {
		int icur = _set[TI(x,y)];
		assert(_heap[icur]._x == x && _heap[icur]._y == y);
		if (icur < 0) return false;
		if (f == _heap[icur]._f) return true;
		bool top = false;
		if (f < _heap[icur]._f) top = true;
		_heap[icur]._f = f;
		_heap[icur]._g = g;
		_heap[icur]._parent = parent;
 
		if (top) {
			move_top(icur);
		}else {
			move_bottom(icur);
		}
 
		//ensure();
		return true;
	}

注意事项：

这也是我实现中犯过的错：

1。移动过程中不能从子节点回到直接父节点，这个是理所当然，所以实现时候在往8个方向移动时要屏蔽父节点。

2。已经在closed中的节点是有可能重新加入opened中的，所以在移动时得到一个新的节点时还要判断是不是比closed中这个节点更cheap（若closed中已经存在这个节点了）。

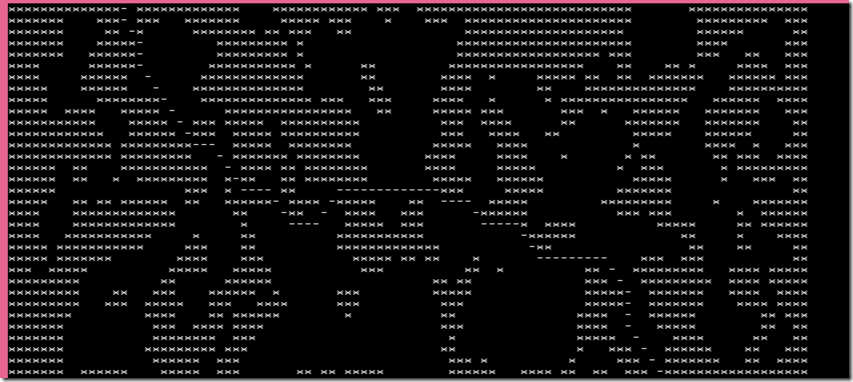
全部代码在此。可以用在游戏地图动态生成中实现的地图来测试A*寻路，下面是在一个35*100的地图中的自动寻路的效果（字符'-'代表路径）