二叉排序树（BST）

二叉排序树（BST）

二叉排序树，又称二叉查找树（BST）

左子树结点值＜根节点值＜右子树结点值

如果用中序遍历来遍历一棵二叉排序树的话，可以得到一个递增的有序数列

左根右

二叉排序树的查找

//二叉排序树结点
typedef struct BSTNode{
    int key;
    struct BSTNode *lchild,*rchild;
}BSTNode,*BSTree;

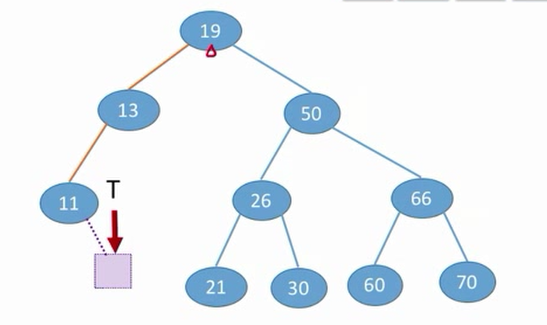
查找是非常方便的，目标值和根节点比较，如果相等则成功，比根节点大往右去，比根节点小往左去。

查找失败就返回null

非递归方式：

//在二叉排序树中查找值为key的结点
BSTNode *BST_search(BSTree T, int key){
    while(T!=NULL&&key!=T->key){ 	//若树为空或等于根节点值，则结束循环
        if(key<T->key){				//小于，则在左子树
            T=T->lchild;
        }else{						//大于，则在右子树
            T=T->rchild;
        }
    }
    return T;
}

最坏空间复杂度=O(1)

递归方式：

//在二叉排序树中查找值为key的结点(递归实现)
BSTNode *BSTSearch(BSTree T,int key){
    if(T==NULL){
        return NULL;						//查找失败
    }
    if(key==T->key){
        return T;							//查找成功
    }else if(key <T->key){
        return BSTSearch(T->lchild,key);	//在左子树找
    }else{
         return BSTSearch(T->rchild,key);	//在右子树找
    }
}

最坏空间复杂度=O(h) 和树的高度相同

二叉排序树的插入

若原二叉排序树为空，则直接插入结点；

否则，若关键字k小于根节点值，则插入到左子树，若关键字k大于根节点值，则插入到右子树。

//在二叉排序树插入关键字为k的新节点（递归实现）
int BST_Insert(BSTree &T,int k){
    if(T == NULL){				//原树为空，新插入的结点为根节点
        T=(BSTree)malloc(sizeof(BSTNode));
        T->key = k;
        T->lchild = T->rchild = NULL;
        return 1;				//返回1，插入成功
    }else if(k == T->key){		//树中不能存在相同关键字的结点，插入失败
        return 0;
    }else if(k<T->key){			//插入到T的左子树
        return BST_Insert(T->lchild,k);
    }else{						//插入到T的右子树
        return BST_Insert(T->rchild,k);
    }
}

最坏空间复杂度=O(h)

二叉排序树的构造

其实就是不断插入新节点的过程

//按照str[]中的关键字序列建立二叉排序树
void Creat_BST(BSTree &T,int str[],int n){
    T = NULL;				//初始化时T为空树
    int i = 0;
    while(i<n){				//依次将每个关键字插入到二叉排序树
        BST_Insert(T,str[i]);
        i++;
    }
}

不同的关键字序列可能得到同款二叉排序树，也可能得到不同款二叉排序树

二叉排序树的删除

先搜索找到目标结点：

（需要保证二叉排序书的特性——左子树结点值<根节点值<右子树结点值）

• 若是被删除的结点z是叶节点，则直接删除，不会破坏二叉排序树的性质。

• 若结点z只有一棵左子树或右子树，则让z的子树称为z父节点的子树，替代z的位置

• 若结点z有左、右两棵子树，则令z的直接后继（或直接前驱）替代z，然后从二叉排序树中删去这个直接后继（或直接前驱），这样就转换成了第一或第二种情况。

进行中序遍历，可以得到一个递增的有序序列。

用右子树最小的值来替代被删除的值（最左下）

用左子树最大的值来替代被删除元素（最右下角）

查找效率分析

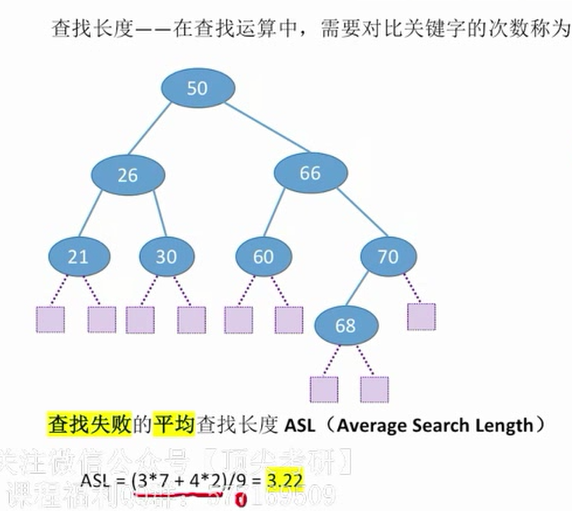
查找长度——在查找运算中，需要对比关键字的次数称为查找长度，反应了查找操作时间复杂度

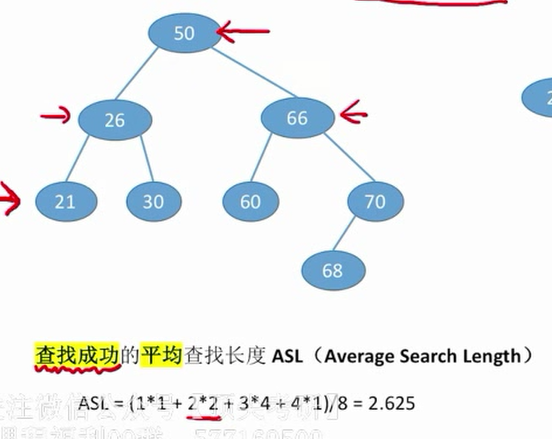
查找成功的平均查找长度ASL（Average Search Length）

若树高h，找到最下层的一个结点需要对比h次

最坏情况：每个节点只有一个分支，树高h=结点数n。平均查找长度=O(n)

最好情况：

n个结点的二叉树最小高度为

\[\lfloor log_2n \rfloor+1
\]

平均查找长度=

\[O(log_2n)
\]

查找失败