[算法]A General Polygon Clipping Library

A General Polygon Clipping Library

Version 2.32 http://www.cs.man.ac.uk/~toby/alan/software/gpc.html

Alan Murta Advanced Interfaces Group Department of Computer Science University of Manchester Manchester M13 9PL, UK

Abstract:

This document describes a C library implementation of a new polygon clipping algorithm. The techniques used are descended from Vatti's polygon clipping method [1]. Subject and clip polygons may be convex or concave, self-intersecting, contain holes, or be comprised of several disjoint contours. It extends the Vatti algorithm to allow horizontal edges in the source polygons, and to handle coincident edges in a robust manner. Four types of clipping operation are supported: intersection, exclusive-or, union or difference of subject and clip polygons. The output may take the form of polygon outlines or tristrips.

Introduction

A generic polygon (or `polygon set') consists of zero or more disjoint boundaries of arbitrary configuration. Each boundary is termed a `contour', and may be convex, concave or self-intersecting. Internal holes may be formed by contour nesting.

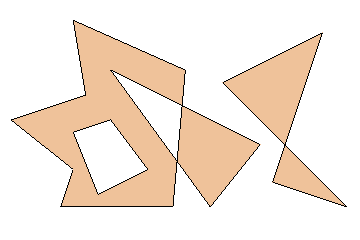Figure 1: A polygon set with four contours.

Figure 1 shows a polygon set comprised of four contours. Over to the left is a seven sided concave contour. Lying completely within it is a four-sided contour, which forms a hole in the surrounding shape. A third, triangular contour intersects the boundary of the first. Finally, over to the right is a disjoint self-intersecting four-sided contour. The interior of the polygon has been shaded for clarity.

The library supports four kinds of clipping (Boolean set) operation: difference, intersection exclusive-or or union of subject and clip polygon pairs. These are illustrated in Figure 2. In each case, the (single) resulting polygon is shown shaded.

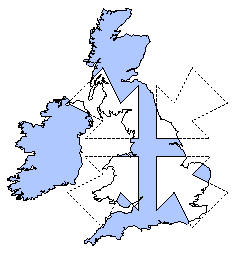
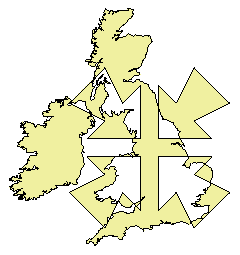
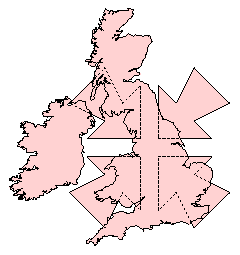Figure 2: Difference, intersection, exclusive-or and union operations.

Recent API changes

The release of Version 2.30 featured some minor changes to the application programmer's interface. These included:

An additional hole field in the gpc_polygon datatype to differentiate hole contours from external contours.
A similar additional hole parameter to gpc_add_contour().
An extra parameter in the gpc_read_polygon() and gpc_write_polygon() functions to specify the polygon datafile format (with or without hole contour flags).

Data types

The generic polygon clipper (gpc) library defines the following structure types for the representation of polygons:

          typedef struct   /* Polygon vertex */

          {

            double            x;

            double            y;

          } gpc_vertex;

          typedef struct   /* Polygon contour */

          {

            int               num_vertices;

            gpc_vertex       *vertex;

          } gpc_vertex_list;

          typedef struct   /* Polygon set */

          {

            int               num_contours;

            int              *hole;

            gpc_vertex_list  *contour;

          } gpc_polygon;

The clipper takes a pair of subject and clip polygons and combines them to form a result polygon. For each contour polygon in the result polygon, the hole value flags whether or not the given contour forms a hole or an external boundary.

Alternatively a collection of tristrips may be generated as the result, this form being more suitable for rendering filled shapes. (The polygon result form is better for drawing outlines, or as intermediate values in multi-clip operations.) Tristrip collections are represented using the following data type:

          typedef struct   /* Set of tristrips */

          {

            int               num_strips;

            gpc_vertex_list  *strip;

          } gpc_tristrip;

Library functions

Eight functions are provided by the library. Two support the reading and writing of data between polygon files and gpc_polygon structures.

          void gpc_read_polygon(FILE        *fp,

                                int          read_hole_flags,

                                gpc_polygon *polygon);

          void gpc_write_polygon(FILE        *fp,

                                 int          write_hole_flags,

                                 gpc_polygon *polygon);

A polygon is stored in an ASCII file using the format:

<num-contours> <num-vertices-in-first-contour> [<first-contour-hole-flag>] <vertex-list>
<num-vertices-in-second-contour> [<second-contour-hole-flag>] <vertex-list>

etc. The hole-flag values are optional, their reading and writing being controlled by setting the second argument of gpc_read_polygon() and gpc_write_polygon() to 1 (TRUE) or 0 (FALSE). Clip operations will correctly set the contour hole flags of the result polygon. This information may be ignored by the user application if it is not required.

For example, a single polygon consisting of a triangular hole within a quadrilateral (with hole flags included) may take the form:

An interactive drawing program may require the ability to construct a polygon contour-by-contour in an incremental fashion. The function gpc_add_contour() facilitates the merging of a new contour with an existing polygon. The final parameter has the value 1 (TRUE) or 0 (FALSE), and indicates whether or not the contour should be considered to be a hole. It is suggested that all contours are initially treated as non-hole (external) contours. Any subsequent clipping operation will set the result polygon hole flags correctly.

          void gpc_add_contour(gpc_polygon     *p,

                               gpc_vertex_list *c,

                               int              hole);

The clipping operation itself is performed by the function

          void gpc_polygon_clip(gpc_op       operation,

                                gpc_polygon *subject_p,

                                gpc_polygon *clip_p,

                                gpc_polygon *result_p);

or, if a tristrip based result is required

          void gpc_tristrip_clip(gpc_op        operation,

                                 gpc_polygon  *subject_p,

                                 gpc_polygon  *clip_p,

                                 gpc_tristrip *result_t);

In both cases the first parameter specifies the clip operation to be performed (namely GPC_DIFF, GPC_INT, GPC_XOR or GPC_UNION). This is followed by subject and clip polygon parameters. The final parameter delivers the result, either as a polygon structure or as a collection of tristrips.

A polygon may be converted to the equivalent tristrip form using the function

          void gpc_polygon_to_tristrip(gpc_polygon   *source_p,

                                        gpc_tristrip *result_t);

Finally, the functions

          void gpc_free_polygon(gpc_polygon *p);

          void gpc_free_tristrip(gpc_tristrip *t);

may be used to release the memory taken up by a polygon or trapezoid on the heap.

Hole and external contours

A contour is classified as an external contour if its uppermost (or rightmost, when the contour top is horizontal) vertex forms an external local maximum (EMX). If this vertex forms an internal local maximum (IMX) the contour is classified as a hole contour.

When contour edges cross (in self intersecting shapes for example) the clipper will always generate a local maximum vertex below the intersection (or when one of the edges is horizontal, to the left of the intersection) which connects the two edge parts which meet at the intersection point from below or from the left. The edge parts which emerge from the opposite side of the intersection point originate from a new local minimum vertex. The closed contours generated by the clipper will never self-intersect.

igure 3: Self-intersecting contours which decompose into an external contour containing a nested hole contour.

These rules have implications with regard to how self intersecting shapes decompose into a set of closed, non-intersecting contours. The intersecting square examples of Figure 3, will each create two nested contours. In each case, the upper / rightmost maximum vertex of the internal contour forms an internal maximum, therefore the contour is classed as a hole (shown dotted). The corresponding outer contour is considered external as it terminates with an external maximum vertex.

Figure 4: Self-intersecting contours which decompose into two touching external contours.

The examples of Figure 4, however, show how similar self intersecting shapes may each create two external contours which touch at the points of intersection. In summary, the contour paths generated by the clipper are affected not only by the shape of the input polygons, but also by their orientation.

Associating holes with external contours

The current version of the clipper merely flags which contours are considered to be holes, and which form external boundaries. Discovering which holes lie within which external contours takes a little more work on the part of the user. One way to associate holes H1, H2 ... Hn with external contours E1, E2 ... Em is to use the clipper to compute the difference of the ith hole Hi and each external contour Ej, for all j from 1 to m. Any difference which gives an empty result indicates that hole i lies within external contour j.

Coincident and near-coincident edges

The clipper will merge edges which are coincident. Adjacent subject and clip contours which share share a common edge will fuse to form a single contour under the union operation, and will produce a null result along their shared boundary under the intersection operation. Numerical precision limits are likely to cause the slight misregistration of coincident edges, resulting in a failure to merge. Increasing the value of the GPC_EPSILON constant in gpc.h will encourage the merging of near-coincident edges. However, incorrect output polygon shapes may result if GPC_EPSILON is given too large a value.

A code example

In the following example program a clip / subject polygon pair is read from an input file. The intersection of these polygons is then calculated, and the result polygon is written to file. Hole classification information is neither read nor written in this example.

          #include <stdio.h>

          #include "gpc.h"

          int main(void)

          {

            gpc_polygon subject, clip, result;

            FILE *sfp, *cfp, *ofp;

            sfp= fopen("subjfile", "r");

            cfp= fopen("clipfile", "r");

            gpc_read_polygon(sfp, 0, &subject);

            gpc_read_polygon(cfp, 0, &clip);

            gpc_polygon_clip(GPC_INT, &subject, &clip, &result);

            ofp= fopen("outfile", "w");

            gpc_write_polygon(ofp, 0, &result);

            gpc_free_polygon(&subject);

            gpc_free_polygon(&clip);

            gpc_free_polygon(&result);

            fclose(sfp);

            fclose(cfp);

            fclose(ofp);

            return 0;

          }

Known bugs

The following problems will hopefully be rectified within subsequent releases. Please see the release notes which follow for bug report procedures.

Non-serious: Tristrip and polygonal output forms will not always be optimal in minimising triangle or vertex counts.

Release notes

This software is Copyright © 1997-1999, Advanced Interfaces Group, Department of Computer Science, University of Manchester. This software is free for non-commercial use. It may be copied, modified, and redistributed provided that the copyright notices which appear within the library source files are preserved on all copies. The intellectual property rights of the algorithms used reside with the University of Manchester Advanced Interfaces Group.

You may not use this software, in whole or in part, in support of any commercial product without the express consent of the author.

There is no warranty or other guarantee of fitness of this software for any purpose. It is provided solely "as is". Although no direct support for the use of this software will be given, bug reports may be sent to gpc@cs.man.ac.uk.

See the VERSIONS.TXT file for a revision history.

References

[1]: Vatti, B.R., "A Generic Solution to Polygon Clipping", Communications of the ACM, 35(7), July 1992, pp.56-63. (Please do not contact us asking for copies of this paper; we are regrettably unable to supply them.)

Back to the gpc home page.