BP神经网络
秋招刚结束,这俩月没事就学习下斯坦福大学公开课,想学习一下深度学习(这年头不会DL,都不敢说自己懂机器学习),目前学到了神经网络部分,学习起来有点吃力,把之前学的BP(back-progagation)神经网络复习一遍加深记忆。看了许多文章发现一PPT上面写的很清晰,就搬运过来,废话不多说,直入正题:
单个神经元
神经网络是由多个“神经元”组成,单个神经元如下图所示:
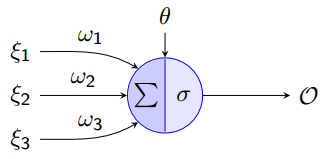
这其实就是一个单层感知机,输入是由ξ1 ,ξ2 ,ξ3和Θ组成的向量。其中Θ为偏置(bias),σ为激活函数(transfer function),本文采用的是sigmoid函数 ,功能与阶梯函数(step function)相似控制设神经元的输出,它的优点是连续可导。
,功能与阶梯函数(step function)相似控制设神经元的输出,它的优点是连续可导。
 是神经元的输出,结果为
是神经元的输出,结果为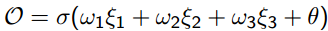
可以看得出这个“神经元”的输入-输出映射其实就是一个逻辑回归,常用的激活函数还有双曲正切函数 。
激活函数
sigmoid:函数

取值范围为[0,1],它的图像如下:
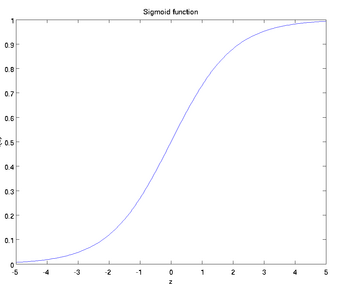
求导结果为:

tanh函数:
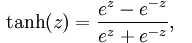
取值范围为[-1,1],图像如下:
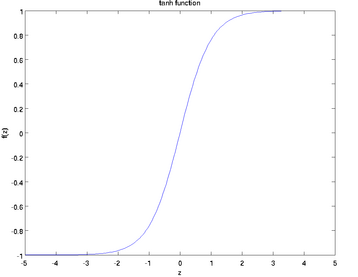
求导数结果为 。本文采用的是sigmoid函数作为激活函数。
。本文采用的是sigmoid函数作为激活函数。
神经网络模型
神经网络将许多“神经元”联结在一起,一个神经元的输出可以是另一个“神经元”的输入,神经元之间的传递需要乘法上两个神经元对应的权重,下图就是一个简单的神经网络:
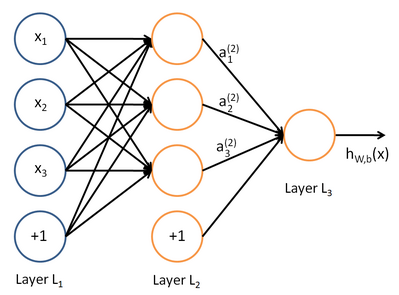
这是一个三层的神经网络,使用圆圈来表示神经元的输入,“+1”被称为偏置节点,从左到右依次为输入层、隐藏层和输出层,从图中可以看出,有3个输入节点、3个隐藏节点和一个输出单元(偏置不接受输入)。
本例神经网络的参数有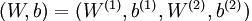 ,其中
,其中 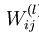 是第l层第 j 单元与 l+1层第
是第l层第 j 单元与 l+1层第  单元之间的联接参数,即:节点连线的权重,本图中
单元之间的联接参数,即:节点连线的权重,本图中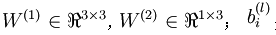 是第l+1 层第i单元的偏置项。
是第l+1 层第i单元的偏置项。
向前传播
机器学习(有监督)的任务无非是损失函数最小化,BP神经网络的原理是前向传播得到目标值(分类),再通过后向传播对data loss进行优化求出参数。可见最优化部分
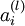 表示
表示 层第
层第  单元激活值(输出值)。当
单元激活值(输出值)。当 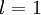 时,
时, 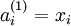 ,也就是第
,也就是第  个输入值。对于给定参数集
个输入值。对于给定参数集 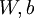 ,
,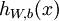 来表示神经网络最后计算输出的结果。上图神经网络计算步骤如下:
来表示神经网络最后计算输出的结果。上图神经网络计算步骤如下:
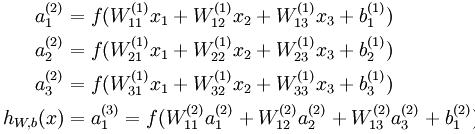
可以看出,神经网络的核心思想是这一层的输出乘上相应的权重加上偏置,带入激活函数后的输出又是下一层的输入。用 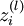 表示第
表示第 层第
层第 单元输入加权和
单元输入加权和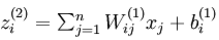 ,则
,则 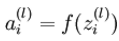 。使用向量化表示方法表示,上面的公式可以简写为:
。使用向量化表示方法表示,上面的公式可以简写为:

这些计算步骤就是前向传播,将计算过程进行推广,给定第  层的激活值
层的激活值 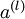 ,第
,第  层的激活值
层的激活值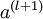 的计算过程为:
的计算过程为:
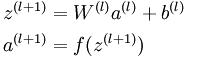
反向传播
在前向传播中,我们得到了神经网络的预测值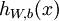 ,这时候可以通过反向传播的方法计算出参数
,这时候可以通过反向传播的方法计算出参数
符号定义
 :第l层第j个节点的输入。
:第l层第j个节点的输入。
 :从第l-1层第i个节点到第l层第j个节点的权值。
:从第l-1层第i个节点到第l层第j个节点的权值。
 :Sigmoid激活函数。
:Sigmoid激活函数。
 ::第l层第j个节点的偏置。
::第l层第j个节点的偏置。
 ::第l层第j个节点的输出。
::第l层第j个节点的输出。
 ::输出层第j个节点的目标值(label)。
::输出层第j个节点的目标值(label)。
使用梯度下降的方法求解参数,在求解的过程中需要对输出层和隐藏层分开计算
输出层权重计算
给定样本标签 和模型输出结果
和模型输出结果 ,输出层的损失函数为:
,输出层的损失函数为:

这其实就是均方差项,训练的目标是最小化该误差,使用梯度下降方法进行优化,对上式子对权重W进行求导:

,整理 ,
,
其中 =
= 带入
带入 ,对sigmoid求导得:
,对sigmoid求导得:

输出层第k个节点的输入 等于上一层第j个节点的输出
等于上一层第j个节点的输出 乘上
乘上 ,即
,即 =
=
 ,而上一层的输出
,而上一层的输出 与输出层的权重变量
与输出层的权重变量 无关,可以看做一个常数,所以直接求导可以得到:
无关,可以看做一个常数,所以直接求导可以得到:
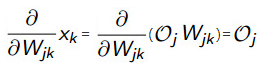
所以将 =
= 带入式子中就得到:
带入式子中就得到:

为了方便表示将上式子记作:

其中:

隐藏层权重计算
采用同样方法对隐藏层的权重进行计算,与前面不同的是关于隐藏层和前一层权重的调整

整理

替换sigmoid函数

对sigmoid求导

把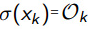 带入进去,使用求导的链式法则:
带入进去,使用求导的链式法则:

输出层的输入等于上一层的输入乘以相应的权重,即: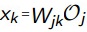 于是得到
于是得到

对 进行求导(
进行求导( =
= ,同样适用于j),
,同样适用于j),

同输出层计算的方法一样,再次利用 ,j换成i,k换成j同样成立,带入进去:
,j换成i,k换成j同样成立,带入进去:

整理,得到:

其中:
我们还可以仿照 的定义来定义一个
的定义来定义一个 ,得到:
,得到:

其中:
偏置调整
从上面的计算步骤中可以看出:例如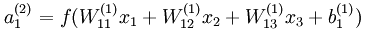 ,偏置节点是不存在对应的权值参数,也就是不存在关于权值变量的偏导数。
,偏置节点是不存在对应的权值参数,也就是不存在关于权值变量的偏导数。
对偏置直接求导:

又有

得到:
 ,其中:
,其中:
BP算法步骤
1. 随机初始化W和b,需要注意的是,随机初始化并是不是全部置为0,如果所有参数都是用相同的值初始化,那么所有隐藏单元最终会得到与输入值相关、相同的函数(也就是说,对于所有  ,
,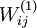 都会取相同的值,那么对于任何输入
都会取相同的值,那么对于任何输入  都会有:
都会有: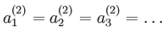 ),随机初始化的目的是使对称失效。
),随机初始化的目的是使对称失效。
2.对每个输出节点按照这个公式计算delta:

3.对每个隐藏节点按照这个公式计算delta:

4.更新W和b的公式为:

并更新参数 ,这里的η是学习率。
,这里的η是学习率。
Reference
2.反向传导算法
BP神经网络的更多相关文章
- BP神经网络原理及python实现
[废话外传]:终于要讲神经网络了,这个让我踏进机器学习大门,让我读研,改变我人生命运的四个字!话说那么一天,我在乱点百度,看到了这样的内容: 看到这么高大上,这么牛逼的定义,怎么能不让我这个技术宅男心 ...
- 数据挖掘系列(9)——BP神经网络算法与实践
神经网络曾经很火,有过一段低迷期,现在因为深度学习的原因继续火起来了.神经网络有很多种:前向传输网络.反向传输网络.递归神经网络.卷积神经网络等.本文介绍基本的反向传输神经网络(Backpropaga ...
- BP神经网络推导过程详解
BP算法是一种最有效的多层神经网络学习方法,其主要特点是信号前向传递,而误差后向传播,通过不断调节网络权重值,使得网络的最终输出与期望输出尽可能接近,以达到训练的目的. 一.多层神经网络结构及其描述 ...
- 极简反传(BP)神经网络
一.两层神经网络(感知机) import numpy as np '''极简两层反传(BP)神经网络''' # 样本 X = np.array([[0,0,1],[0,1,1],[1,0,1],[1, ...
- BP神经网络
BP神经网络基本原理 BP神经网络是一种单向传播的多层前向网络,具有三层或多层以上的神经网络结构,其中包含输入层.隐含层和输出层的三层网络应用最为普遍. 网络中的上下层之间实现全连接,而每层神经元之 ...
- BP神经网络学习笔记_附源代码
BP神经网络基本原理: 误差逆传播(back propagation, BP)算法是一种计算单个权值变化引起网络性能变化的较为简单的方法.由于BP算法过程包含从输出节点开始,反向地向第一隐含层(即最接 ...
- 机器学习(一):梯度下降、神经网络、BP神经网络
这几天围绕论文A Neural Probability Language Model 看了一些周边资料,如神经网络.梯度下降算法,然后顺便又延伸温习了一下线性代数.概率论以及求导.总的来说,学到不少知 ...
- 基于Storm 分布式BP神经网络,将神经网络做成实时分布式架构
将神经网络做成实时分布式架构: Storm 分布式BP神经网络: http://bbs.csdn.net/topics/390717623 流式大数据处理的三种框架:Storm,Spark和Sa ...
- BP神经网络算法学习
BP(Back Propagation)网络是1986年由Rumelhart和McCelland为首的科学家小组提出,是一种按误差逆传播算法训练的多层前馈网络,是眼下应用最广泛的神经网络模型之中的一个 ...
随机推荐
- 高性能Web服务器Nginx的配置与部署研究系列(1)-- 入门 hello work
简介: Nginx 是一个基于 BSD-like 协议.开源.高性能.轻量级的HTTP服务器.反向代理服务器以及电子邮件(SMTP.POP3.IMAP)服务器.Nginx 是由一个俄罗斯的名叫“Igo ...
- CALayer 3 详解 -----转自李明杰
CALayer3-层的属性 本文目录 一.隐式动画属性 二.position和anchorPoint 回到顶部 一.隐式动画属性 * 在前面几讲中已经提到,每一个UIView内部都默认关联着一个C ...
- linux之PATH环境变量
在linux中,我们发现一些命令在任何目录都能执行,并不会出现找不到这个命令文件的提示,这其中就是PATH变量帮我们定位的!首先我们来查看一下PATH变量 [root@localhost /]# ec ...
- 浅谈对ionic项目的理解
在思考怎么将客户端app连接到服务器的时候,就在想ionic项目的本质是什么,一开始因为ionic serve这一命令,我以为它自己就是个服务器,但是后来一细想又感觉不是这样,不然客户端又该怎么和服务 ...
- Bootstrap<基础十五> 输入框组
Bootstrap 支持的另一个特性,输入框组.输入框组扩展自 表单控件.使用输入框组,可以很容易地向基于文本的输入框添加作为前缀和后缀的文本或按钮. 通过向输入域添加前缀和后缀的内容,您可以向用户输 ...
- number 数据类型的分析。
在js中,number数据类型可能算最令人关注的的类型之一了. number类型分为整数和浮点数. 一,整型数,整型又分为十进制,八进制,十六进制. 十进制即是生活中接触到的:而八进制数的首位必须是零 ...
- 动态加载jQuery
success: function(data){ for(var i in data){ $('.x-details>ul:eq(0)').append("<li>&quo ...
- IOS中的Block与C++11中的lambda
ios中的block 可以说是一种函数指针,但更确切的讲,其实际上其应该算是object-c对C++11中lambda的支持或者说是一个语言上的变体,其实际内容是一样的,C++的lambda我已经有简 ...
- MyBatis3学习--来源自用户指南
MyBatis是什么? MyBatis 是一款一流的支持自定义SQL.存储过程和高级映射的持久化框架. MyBatis几乎消 除了所有的JDBC 代码,也基本不需要手工去设置参数和获取检索结果. My ...
- android studio使用中遇到的问题
旧版和新版切换会报错(点击更正, 不影响程序使用) 2.debug正常, 打包签名程序时候报错 String index out of range: -82 java.lang.StringIndex ...
